自动学习(AutoML)——元学习建模
自动学习(AutoML)——元学习建模
在之前的文章中,我们主要描述的是元学习的基本形式和小样本中的元学习,进行我们来介绍元学习的基本建模思想和建模实例。
1 元学习建模
1.1 从传统到元学习
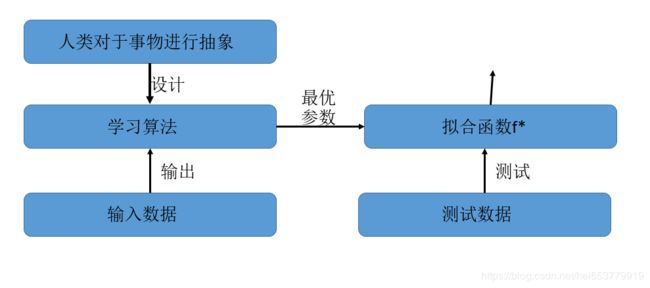
在传统的机器学习中,我们的建模方式通常是由人来决定的,也就是说通过人来对事物进行抽象,然后设计一套关于该任务的框架,进而将数据投入到该框架中进行学习。最后获取到相关的参数。这些参数可以拟合出来一个函数 f ∗ f^* f∗,然后用这个拟合出来的函数来进行测试,如果效果符合我们的预期,那么说明这个模型是有效的,能够解决我们的实际需求的。求流程如下图所示:
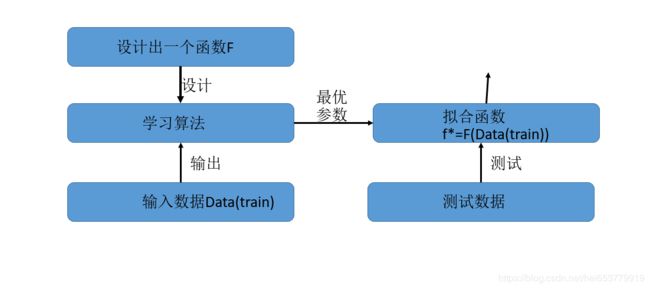
而元学习的目标是将由人设计的学习算法,改成由机器进行设计。其流程如下所示:
如上图所示,在元学习中,训练数据是一系列的Data(train),根据这些训练数据来生成多个 f ∗ f^* f∗,机器求解的目标不在是当个的最佳拟合函数 f ∗ f^* f∗,而是为求解新的函数F,这个F决定了在给定Data(train)的情况下如何生成 f ∗ f^* f∗。
总结一下,在传统的机器学习中,学习的目标是生成一个最佳的拟合函数 f ∗ f^* f∗,而在元学习中,目标是寻找一个如何生成 f ∗ f^* f∗的方式。
1.2 元学习模型搭建过程
在理解了元学习模型搭建的基本思路之后,我们下面来给出模型搭建过程的描述。
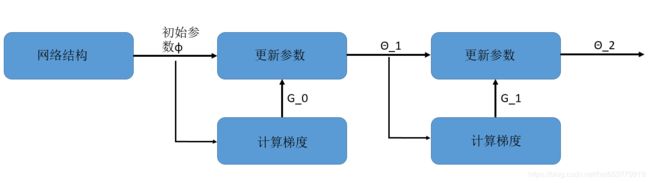
首先,肯定是如何准本训练资料,在前面我们提到过,在元学习中,会存在一系列的Data(train),显然这一系列的数据是事先准备好的。所以,我们将目标放在了一系列的 f ∗ f^* f∗上。事实上, f ∗ f^* f∗本身也是一组最佳的参数,这一组最佳的参数应该如何获得呢?我们不妨从基本的网络结构看起:
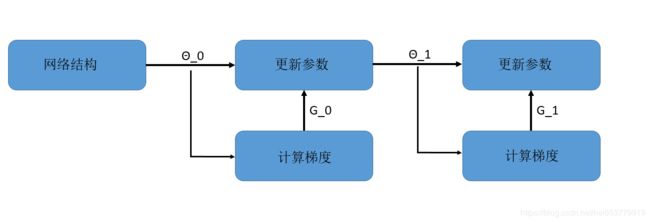
上图所示的是一个基本的参数更新的过程,通过不断的进行迭代,我们最后可以获取到一组最优的参数来拟合出一个最佳的函数 f ∗ f^* f∗。根据上面的训练过程,我们能够确定,当我们使用不同的网络结构,或者使用了不同的参数进行初始化,或决定了不同的参数更新方式的时候,我们就可以生成不同的最优参数,也就是可以成不同的最佳拟合函数 f ∗ f^* f∗。所以,我们针对梯度下降算法来看,元学习的最终成功是在给点一系列训练资料的情况下,机器能够找到针对这些资料的SGD最佳的训练流程( f b e s t ∗ f_{best}^* fbest∗)。因此,为元学习准备的 f ∗ f^* f∗,实际上是由包含尽量多和丰富的组合方式的不同训练流程来组成的。
在作为准备之后,正如上面所说,我们的目标是找到最优的 f b e s t ∗ f_{best}^* fbest∗,下一步要做的就是设计评价函数F寻找能力好坏的指标。具体来讲,F可以选择各种不同的训练流程 f ∗ f^* f∗,如何评价F找到的现有流程 f ∗ f^* f∗,以及如何提升 f ∗ f^* f∗,这是元学习中比较核心的一个部分。
首先,我们想到找到一个最优的函数F,一般从其损失函数看起,通过损失函数的优化,可以进一步对函数F进行优化。下面我们从损失函数看起:
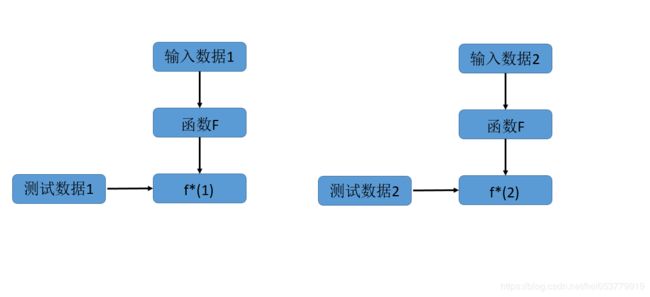
首先,我们来看根据函数F和两个不同的输入数据来生成的最优函数 f 1 ∗ , f 2 ∗ f^*_1,f^*_2 f1∗,f2∗,对这两个子任务,我们是由T1和T2进行表示,通过训练过程生成的Loss值使用L1和L2进行表示。最终,我们就可以将损失定义为在所有子任务上的损失和。用公式表示就是:
L ( F ) = ∑ n = 1 N L n L(F)=∑_{n=1}^NL^n L(F)=n=1∑NLn
在定义完损失函数之后,我们下一步就是降低这种损失来获取最优的F。
2 元学习建模实例 MAML
2.1 MAML引入
简单的回顾一下,我们之前提到的关于元学习的建模过程,元学习的过程是通过函数F来生成某一个任务的f。这个f是关于子任务的一个拟合函数。我们通过这个拟合函数来实现对于子任务的解决。对于函数f是如何解决的,可以有很多的方式,这里我们给出最为简单的方式,f负责决定参数的赋值方式,而不去设计模型的架构,也不改变参数更新的方式,也就是说,f对应的网络结构是事先确定好的,,MAML要解决的是如何针对不同的任务为网络赋予不同的初始值。我们用一张图来描述f的作用。
如上图所示,f只需要考虑参数的初始化方式,假设当前参数的初始化为φ,将φ应用于所有的训练任务之中,并将所有任务的最终训练结束之后的参数记为 θ n ∗ θ^*_n θn∗(n表示第n个任务),然后该参数下的损失记为 l n ( θ n ∗ ) l_n(θ^*_n) ln(θn∗),则当前的初始化参数φ的损失函数就可以表示为:
L ( φ ) = ∑ n = 1 N L n ( θ n ∗ ) L(φ)=∑_{n=1}^NL_n(θ^*_n) L(φ)=n=1∑NLn(θn∗)
接下来就是对于参数φ的误差进行反向传播,最终的结果为:
φ ∗ = a r g m i n φ L ( φ ) φ^*=argmin_φL(φ) φ∗=argminφL(φ)
将φ放入到梯度下降算法中,就可以得到:
φ n e w = φ − η ▽ φ L ( φ ) φ_{new}=φ-η▽_φL(φ) φnew=φ−η▽φL(φ)
现在,我们来分析上面这种方式存在的问题,一个元学习器而言吗,其内部必然存在很多的子任务,如果我们对于每一个子任务都都要进行迭代到最优参数。这显然是一个非常耗时的情况。为了解决改善这个问题,MAML提出一个加快的解决方法,对于每一个子任务,其只进行一次迭代,计算方式如下图所示:
θ n ∗ = φ − ε ▽ φ L n ( φ ) θ_n^*=φ-ε▽_φL_n(φ) θn∗=φ−ε▽φLn(φ)
能够这样做的原因在于如果模型只需要一次训练就能到达最优的相关,那么训练的初始参数基本能够符合最优的参数。
进一步,我们从F本身的损失函数来看:
▽ φ L n ( φ ) = ▽ φ ∑ n = 1 N L n ( θ n ) = ∑ n = 1 N ▽ φ L n ( θ n ) ▽_φL_n(φ)=▽_φ∑_{n=1}^NL_n(θ_n)=∑_{n=1}^N▽_φL_n(θ_n) ▽φLn(φ)=▽φn=1∑NLn(θn)=n=1∑N▽φLn(θn)
我们不妨来对上述公式进行展开,则有:
▽ φ L n ( θ ∗ ) = ∂ L ( θ ∗ ) ∂ φ 1 ∂ L ( θ ∗ ) ∂ φ 2 ∂ L ( θ ∗ ) ∂ φ 3 . . . ∂ L ( θ ∗ ) ∂ φ n ▽_φL_n(θ^*)=\begin{matrix}\frac{∂L(θ^*)}{∂φ_1}\\ \frac{}{}\\ \frac{∂L(θ^*)}{∂φ_2}\\ \frac{}{}\\ \frac{∂L(θ^*)}{∂φ_3}\\ .\\ .\\ .\\ \frac{∂L(θ^*)}{∂φ_n}\end{matrix} ▽φLn(θ∗)=∂φ1∂L(θ∗)∂φ2∂L(θ∗)∂φ3∂L(θ∗)...∂φn∂L(θ∗)
对于某一轮迭代使用的 φ i φ_i φi而言,其对应生成了所有的子任务的参数 θ i ∗ θ^*_i θi∗,然后,又由这些子任务的参数来生成了关于函数F的损失情况。因此,我们可以进一步对上面的式子进行简化来分成两个部分:
∂ L ( θ ∗ ) ∂ φ i = ∑ j ∂ L ( θ ∗ ) ∂ θ j ∗ ∂ θ j ∗ ∂ φ i \frac{∂L(θ^*)}{∂φ_i}=∑_j\frac{∂L(θ^*)}{∂θ_j^*}\frac{∂θ^*_j}{∂φ_i} ∂φi∂L(θ∗)=j∑∂θj∗∂L(θ∗)∂φi∂θj∗
很明显,第一个部分是很好进行计算的,所有我们直接来看后一项,我们将 θ j ∗ θ^*_j θj∗带入到参数更新公式,则有:
θ j ∗ = φ j − ε ∂ L ( φ ) ∂ φ j θ^*_j=φ_j-ε\frac{∂L(φ)}{∂φ_j} θj∗=φj−ε∂φj∂L(φ)
可以注意到,当i≠j的时候,有:
∂ θ j ∗ ∂ φ i = − ε ∂ L ( φ ) ∂ φ j ∂ φ i \frac{∂θ^*_j}{∂φ_i}=-ε\frac{∂L(φ)}{∂φ_j∂φ_i} ∂φi∂θj∗=−ε∂φj∂φi∂L(φ)
当i=j的时候则有:
∂ θ j ∗ ∂ φ i = 1 − ε ∂ L ( φ ) ∂ φ j ∂ φ i \frac{∂θ^*_j}{∂φ_i}=1-ε\frac{∂L(φ)}{∂φ_j∂φ_i} ∂φi∂θj∗=1−ε∂φj∂φi∂L(φ)
这里出现了二次微分,为了简化计算,在MAML中提出了将二次微分项直接舍弃,则有了:
∂ θ j ∗ ∂ φ i = { 0 i ≠ j 1 i = j \frac{∂θ^*_j}{∂φ_i}=\begin{cases}0&i≠j\\1&i=j\end{cases} ∂φi∂θj∗={01i=ji=j
则,最终的计算为:
∂ L ( θ ∗ ) ∂ φ i = ∑ j ∂ L ( θ ∗ ) ∂ θ j ∗ ∂ θ j ∗ ∂ φ i ≈ ∂ L ( θ ∗ ) ∂ θ j ∗ \frac{∂L(θ^*)}{∂φ_i}=∑_j\frac{∂L(θ^*)}{∂θ_j^*}\frac{∂θ^*_j}{∂φ_i}≈\frac{∂L(θ^*)}{∂θ_j^*} ∂φi∂L(θ∗)=j∑∂θj∗∂L(θ∗)∂φi∂θj∗≈∂θj∗∂L(θ∗)
则最开始的展开式变成了:
▽ φ L n ( θ ∗ ) = ∂ L ( θ ∗ ) ∂ φ 1 ∂ L ( θ ∗ ) ∂ φ 2 ∂ L ( θ ∗ ) ∂ φ 3 . . . ∂ L ( θ ∗ ) ∂ φ n = ∂ L ( θ ∗ ) ∂ θ 1 ∗ ∂ L ( θ ∗ ) ∂ θ 2 ∗ ∂ L ( θ ∗ ) ∂ θ 3 ∗ . . . ∂ L ( θ ∗ ) ∂ θ n ∗ = ▽ θ ∗ L n ( θ ∗ ) ▽_φL_n(θ^*)=\begin{matrix}\frac{∂L(θ^*)}{∂φ_1}\\ \frac{}{}\\ \frac{∂L(θ^*)}{∂φ_2}\\ \frac{}{}\\ \frac{∂L(θ^*)}{∂φ_3}\\ .\\ .\\ .\\ \frac{∂L(θ^*)}{∂φ_n}\end{matrix}=\begin{matrix}\frac{∂L(θ^*)}{∂θ_1^*}\\ \frac{}{}\\ \frac{∂L(θ^*)}{∂θ_2^*}\\ \frac{}{}\\ \frac{∂L(θ^*)}{∂θ_3^*}\\ .\\ .\\ .\\ \frac{∂L(θ^*)}{∂θ_n^*}\end{matrix}=▽_{θ^*}L_n(θ^*) ▽φLn(θ∗)=∂φ1∂L(θ∗)∂φ2∂L(θ∗)∂φ3∂L(θ∗)...∂φn∂L(θ∗)=∂θ1∗∂L(θ∗)∂θ2∗∂L(θ∗)∂θ3∗∂L(θ∗)...∂θn∗∂L(θ∗)=▽θ∗Ln(θ∗)
之后的过程就是一个嵌套迭代的过程,首先第一个一个 φ 0 φ_0 φ0,然后基于 φ 0 φ_0 φ0和第一个任务T1来进行训练,最后获得最优的参数 θ m ∗ θ^*_m θm∗,然后计算其梯度,将关于 θ m ∗ θ^*_m θm∗的梯度用于调节 φ 0 φ_0 φ0,对φ进行更新生成 φ 1 φ_1 φ1,然后在下一个子任务T2上进行训练,如此嵌套迭代,最后在所的子任务训练结束之后,我们的就可以获得最终的 φ n φ_n φn
2.2 总结
在上面的描述中,我们重点介绍了关于元学习的建模过程和一个建模实例,当然元学习的功能不仅于此,其还能够学习如何设计模型框架,如何设计参数更新策略,如何设计激活函数等等,这些内容我们会在之后的文章介绍。
3 参考
1.【学习笔记】元学习(Meta Learning)学习笔记