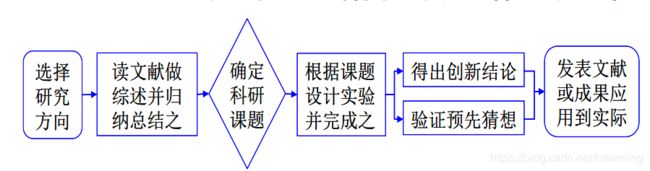
数学建模—从起点到终点

主要流程

【该图源自科学研究流程】

主要参考资料

• 学位论文 
• 搜索引擎
• 会议论文、期刊、专利

评分细则

• 摘要——精炼简洁【最为重要】【针对什么问题、使用什么方法、得到什么结论】
• 思路创新、标题创新【其次重要】
• 完整的解题思路与建模过程
• 描述的准确度与清晰度
• 赛题解读
• 题目的模糊概念的必要澄清
• 明确列出所有前提与假设，及其合理性解释或论证
• 建模的动机或论证模型的合理性
• 有效、合理的模型
• 稳性测试：灵敏度分析、稳健性分析
• 讨论优缺点
• 给出清晰的结论

排版写作

• 写作资料：文献检索及Word排版.pdf
• 画图资料：Chap1.mlx 

编程

• 常用数据处理方法：常用数据处理方法.pdf
• 典型分布曲线：https://blog.csdn.net/ljyljyok/article/details/81624496
• 函数拟合：https://blog.csdn.net/laobai1015/article/details/77537145
• 函数查询：help 或 https://www.mathworks.com/ 或 https://ww2.mathworks.cn/
• 模型：《数学建模算法与应用》

常用建模算法

• 层次分析法

1. 适用题目：评估【主观赋权】
2. 概念：https://zhuanlan.zhihu.com/p/38207837【加权平均、确定权重、无数据时适用】
3. 类似（均为有数据时适用）：熵权法、标准差法、CRITIC法、模糊综合评判理论法

• 回归

1. 推广：时间序列【适用于短期预测】

• 灰色预测

1. 适用题目：预测，数据少
2. 优点：不需要很多数据，能生成规律性较强的序列，精度高
3. 缺点：只适合中短期预测，指数预测

• 线性规划

1. 适用题目：带约束的优化问题、指派问题
2. 求解：linprog 或 蒙特卡洛法 或 bintprog
3. 推广：整数规划

• 非线性规划

1. 使用题目：带非线性约束的最优化问题、飞行管制问题
2. 函数：fmincon 等

• 目标规划

1. 适用题目：多目标规划
2. 求解：加权系数法，优先等级法，序贯算法，数据包络分析【层次分析类似】

• 微分方程求解

1. 适用题目：预测、连续变化
2. 列式：确定要研究的量，与之相应的基本规律或定理，列式【SEIR,logistics】
3. 优点：能反映相关关系，精度高，易改进
4. 缺点：中长期偏差微大，结果难求

• 排队论方法

1. 适用题目：排队等待时间

• 元胞自动机

1. 适用题目：交通问题、仿真模拟扩散

• 图论

1. 适用题目：最短路、pagerank、最小生成树、网络最大流问题、最小费用最大流问题、旅行商问题、计划评审与关键路径、钢管采买问题
2. 方法：dijkstra、Floyd、prim，kruskal，标号法，改良圈算法，

• SVM

1. 适用题目：分类

• 聚类算法

1. 适用题目：分类、指标降维

• 主成成分分析

1. 适用题目：判断部分指标是否能代替综合指标【降维】【客观赋权】
2. 弊端：受量纲的影响
3. 推广：因子分析【更为抽象】—>更进优化有：对应分析【样本对应变量相关性】

• 判别分析

1. 适用题目：统计学分类
2. 概述：根据个体观测指标判断个体所属类别【统计方法】

• 多维标度法

1. 适用题目：由模糊指标绘制客体图形并揭示关系

• 偏最二小回归

1. 适用题目：多个变量预测另一组多个变量

• 优化算法

1. 遗传算法
2. 模拟退火算法

• 其他

1. 链接：https://blog.csdn.net/weixin_43107805/article/details/89069182?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task

美赛题型

外刊链接

• https://www.sciencedirect.com/search/advanced
• https://www.scilit.net/advanced
• https://sci-hub.tw/

了解数学与数学模型

数学演绎推理，数学模型是归纳演绎，一个从原理到结论，一个从现实到规律。归纳是演绎的基础，演绎是归纳的指导。数学建模从现实到理论，再从理论反哺回实践。

模型优劣评判标准：是否具有一定实际背景、假设是否合理、推理是否正确、方法是否简单、论述是否深刻。

队友选择

• 选择有论文写作经验或是曾仔细研读论文的队友：

这样的队友对论文语言描述会比较了解，对格式要求也比较明确，这次两个队友对论文的引用与语言的描述十分不理解，其中负责撰写论文的用了很多复杂长语句，而让一个辅助的同学找的论文引用格式十分不标准，导致后期需要花费大量时间去重新调整，甚至只能再让别的队友重新处理一遍。

• 选择逻辑思维较为清晰的队友

在比赛的时候，负责我们写作的队友经常出现了文章前后不一致的情况，每个小块能描述的不错，但是从文章整体层面上来块却无法很好的衔接，存在描述顺序混乱的情况。

• 选择能把握重点、能明确目标的队友

在整个比赛过程中，有一个队友常常不能把握好我们现在应该做什么，需要找什么样的资料才能有所帮助。例如：需要参考别人运用到了什么方法与模型，然后找了一堆没有任何参考意见的叙述意义的论文。再有，我们现在要将某个东西运用下去，然后其依旧在不断的提出新的点子，甚至有些东西与我们要做的东西毫无关系。

• 选择有耐心、负责任的队友

在短时间内写好一篇论文，需要持续的做大量的工作。在翻译阶段，原先我们计划是用机器粗翻，而后再用人工细调。负责我们翻译的同学起先能逐句检查，但翻译了五分之一不到的篇幅之后，就开始不耐烦的直接选用而不检查。此外，更有甚者为了完成我们给他的任务，用了一些完全不可用的东西以次充好，比如说我提出的给论文的修改意见，最后整合的同学把我的意见也当作正文去使用。在我看来，当任务不是无法完成时，以次充好<不做事<做好。以次充好浪费的不光是当事人的时间，还是浪费看残次品人的时间。

• 选择有一定数学知识储备的作为队友

数学至少要达到能看懂模型理论依据与描述的水平，不要那种自己找的一堆看不懂的模型，然后用不切实际的话来描述它非常好，能怎么用的队友。更不要那种我们用的方法都看不懂的人，否则你极有可能在时间极少的情况下还得教会它看懂。。

• 选择专业不同的队友

选择专业领域不同的队友在选题与提出解决方案上会更有优势，在这次比赛时，我们一开始选择了B题，但是不论在找资料的过程，还是看资料的时候都有非常大的困难，能找到的关键词也就沙雕最为贴切了。

• 选择能力互补的队友

我认为一个优秀的团队不是队里有一个人十全十美，而是队友互相各自都有自己的长处，相互补足合作能达到1+1大于2的效果，当然队里有个全能型大佬是最好不过了。一定要明确队里每个人的优势在哪里，并且最好让每个都能负责自己熟悉的东西。当然在别的方面也不要一篇空白做小白，多少也要了解一些，至少在人需要帮助的时候能贡献自己的一份力量。

• 选择有总结能力或是具有较强理解能力的队友

建模的过程就是理解问题，总结问题要点，查阅理解别人的论文，总结别人的方法与观点，再自己运用，总结评价自己的东西，让它变得更好，如此反复。

• 选择有自知之明的队友

知道自己的弱点，不去干预别人的强项，懂得自己能做好什么，什么需要别人什么样的帮助，知道自己的极限，做实事与学习、实验不同，应该量力而行。当然不是说不允许提出质疑或是方案，而是在别人否决时依然坚持自己幼稚的想法，外行人评价内行人本来就是个愚蠢的行为。

• 选择乐观的队友

建模是个很磨人的事情，对脑力与体力都有着不小的挑战，懂得苦中作乐会让自己稍微开心一些，讲讲笑话幽默一点对团队氛围与团结都很有好处。

• 选择懂得妥协的队友

固执己见往往听不进别人的意见，尤其在只能选择一个结果时，还有可能会发生争执冲突，只要不是原则性错误，听一下别人的也没啥，只要别人说的在理，也许在你看起来好像不得行，但是在别人看来却是不错，更重要的是能避免不必要的时间消耗，毕竟美赛时间是非常有限的。

自己的要求

俗话说，己所不欲勿施于人，在要求别人的同时也要同样的要求自己，上面对队友选择上的描述同样也是对自己的要求。

• 心态

乐观、自信：要相信自己能做好，要相信自己能在规定的时间完成，要相信自己能得奖，才会有动力去冲冲冲。

懂得妥协、学会倾听、懂得变通：要听取别人的意见，善于倾听，懂得取长补短，不固执己见，多方汲取，会有更好的方案。在恰当的时候让步，有助于推进团队进度，不会死卡在一个地方停滞不前，在有限的时间争取珍惜每一分钟，不要把时间浪费在争执上。

相信队友：还是那句话，这不是一个人的比赛，这份相信是双向的，交给队友的任务就应该相信他能做好，这样才能安心做自己的，也让队友能安心做他自己的。但是相信也不是盲目的相信，不乏有因为各种原因造成的缺漏，所以一定要复盘，不光复盘队友的，也要确认自己的，在做事的时候完全相信队友，在复盘的时怀揣怀疑的目光去审视。

耐心、负责：耐心与负责其实是相辅相成的。有了一颗负责任的心，就能压制住自己暴动的心，有了一份耐心，也能更好的对自己负责，慢工出细活，稳中求健，先把手头事情做好，明确自己现阶段做的什么事儿，因阶段制宜。

• 技能

与自己需要做的事情相关。建模的就注意提升自己的数学能力，模型敏感度。写代码的就提升自己的编码、修改、复现能力。写作的就提高自己的写作、架构搭建、语句描述等能力。提前根据自己要做的事去提高自己。

比赛历程

我们参加比赛其实是个临时决定，半路出家，准备的时间其实非常短，统共就无经验的参加了一次模拟赛，然后赛前突击了几天就火急火燎的去比赛了。第一次模拟赛，我们并没有特别重视，就单纯为了体验一下整个建模的流程，总的来说就是老年养生赛，没有熬夜，也没有持续工作，中午甚至还能午休。虽说我们参加的不是很正规，甚至最后自己写的都没提交，但是也经过一次让我们清楚了各自的能力有多少，同样也总结了一下整个流程中我们的问题，顺便大致计划了一下各自的职能，我主要负责建模、打代码、排版，另一个负责写作、翻译，剩下一个因为能力确实不济就让他辅助了。然后我就开始根据每个人能力制定了一个训练计划，但是好像强度有点高，他们有点受不了，最后大概一半没完成，但是我觉得这个训练计划还是非常有必要的，小白参赛确实会吃很大的亏。到比赛那天早上7点正式开始，虽然本来比赛是六点开始的，我们想着老人家还是要好好休息的，不用太血气方刚，然后就再没舒服的睡觉过。一天平均睡6个小时，最后一天还通宵了，确实是精神爽。之后就是初步选题，找资料，然后好像过分超纲了，就再换了个，再找资料。这个过程很快，就大概一小时多就选好了。然后就开始辛苦历程，因为疫情我们是云建模沟通还是蛮困难的。先是各自看题，对这个题目有了个整体印象，然后就开始讨论题目要求，每个人出一下思路，决定好之后就开始了。一个人列大纲，我开始找资料解决问题，另一个人就帮忙找资料、找数据。之后到了晚上，一起看论文成果，提出修改意见，到现在空有思路，数据一直不到位，强行造出一个超级化简版模型并编码。第二天，写论文的继续写。找数据的接着找。自己找了资料、数据改良了第一个模型，完成第二个模型，设计第三个模型。第二天成果：第二问完成一半，缺代码。第三天，写论文的继续写，并找了一些资料辅助建模。找资料的继续找，找了一些定义辅助建模，并辅助写作同学画图。建好所有模型，进行测试。第四天，画图，改良模型，大家一起写论文，然后排版翻译改图，通宵，欢聚一声开始睡觉！

训练计划

因为我们是散装组合，没有老师可以依赖，只能自己练自己。计划大致可以分两个阶段，第一阶段是佛系养生阶段，第二阶段就是冲刺阶段。

第一阶段：这个阶段其实没太认真的计划，就让每个人每两天看一篇o奖论文，并且总结，看看别人比赛的经验，每两天小讨论一下。然后我额外让自己多熟悉熟悉matlab编程，毕竟我接触matlab不到4天，就模拟赛的时候学了一下。让其中另一个人恶补一下数学知识，毕竟他数学基础实在是太差了，虽然他没听组织安排玩了好一阵子，啥也没看。然后就开始悠闲备赛，刚写了两篇总结后就突然发现要开始比赛了，我当机立断，不能悠闲了，得开始肝，于是我就找了个美赛课程，以及一堆材料（论文写作、matlab使用、历年美赛信息）和一些数学建模的书，最后只看了一本《数学建模算法与应用》，不得不说这本书确实很棒，然后就开始了第二阶段。

第二阶段：

第一天

A	看美赛课程，看数学建模书	大致学习美赛所有相关技能，了解相关模型
B	看论文写作相关资料，看五篇o奖并总结	了解论文是怎样写作的
C	装一下latex，看五篇o奖引用相关，找一份模板	为其学习排版铺垫，以及如何查资料与数据【后来发现他又偷懒了】
可选	看别人美赛总结【不得不说，看别人总结非常有帮助】
必选	一个模拟赛分析的讲座	因为我们参与过，能评价我们模拟成果对比别人是咋样的，事实证明好像没啥用，就让我们更有信心了

第二天

A	专注看书、加一篇论文	熟悉某类题型，外加看书继续学习模型实现
B	看三篇不同题型的论文摘要与问题重述	学习如何写摘要与理解问题
C	学习matlab绘图，找数据资源，总结引用格式	方便辅助我改图，以及提前了解自己的职责【又偷懒】
可选	多看几篇

第三天

A	持续看书
B	制定论文通用框架与模板	先决定好每个地方需要写啥，初步制定架构
C	学习latex部分功能	辅助后期排版【持续偷懒中】

 

 

总结参考：

https://blog.csdn.net/weixin_42815609/article/details/104261652?utm_source=app

https://blog.csdn.net/qq_41149269/article/details/86881902

写作：https://blog.csdn.net/m0_37243869/article/details/103887466?utm_source=app

写作：https://blog.csdn.net/qq_40481843/article/details/86692343