用Python实现二叉树、二叉树非递归遍历及绘制
前言
关于二叉树的实现与遍历,网上已经有很多文章了,包括C, C++以及JAVA等。鉴于python做为脚本语言的简洁性,这里写一篇小文章用python实现二叉树,帮助一些对数据结构不太熟悉的人快速了解下二叉树。本文主要通过python以非递归形式实现二叉树构造、前序遍历,中序遍历,后序遍历,层次遍历以及求二叉树的深度及叶子结点数。其他非递归形式的遍历,想必大多人应该都很清楚,就不再声明。如果你用C或者C++或者其他高级语言写过二叉树或者阅读过相关方面代码,应该知道二叉树的非递归遍历避不开通过栈或者队列实现。是的,python也一样。但是python自带的list功能很强大,即可以当stack 又可以当成queue。 这样用python实现二叉树就可以减少了对栈或者队列的声明及定义。
实现
二叉树的结点的实现
如上图1的的二叉树,要想实现二叉树。首先应该先声明一个二叉树结点,包括它的元素及左右子结点,这个在C/C++也是一样的。在python里, 可以通过类声明一个结点,如下:
class BiNode(object):
"""class BiNode provide interface to set up a BiTree Node and to interact"""
def __init__(self, element=None, left=None, right=None):
"""set up a node """
self.element = element
self.left = left
self.right = right
def get_element(self):
"""return node.element"""
return self.element
def dict_form(self):
"""return node as dict form"""
dict_set = {
"element": self.element,
"left": self.left,
"right": self.right,
}
return dict_set
def __str__(self):
"""when print a node , print it's element"""
return str(self.element)上述的dict_form interface是将结点以python字典的形式呈现出来,方便后面将树打包成字典。另外说明下由于python字典的特性,将字典当成一个树结构来处理也是可以的。事实上,很多人是这样做的。下图测试展现了树结点的实现:

二叉树初始化
实现了二叉树结点,接下来实现二叉树.首先对二叉树进行初始化,代码如下:
class BiTree:
"""class BiTree provide interface to set up a BiTree and to interact"""
def __init__(self, tree_node=None):
"""set up BiTree from BiNode and empty BiTree when nothing is passed"""
self.root = tree_node`
上面代码很简单,就是对树通过一个传进来的结点进行初始化,如果参数为空则初始化为一个空树。
顺序构造二叉树
那么我如果想通过一个列表元素按顺序实现树的构造或者通过字典进行构造呢?
先说下用一个列表元素按顺序构造。
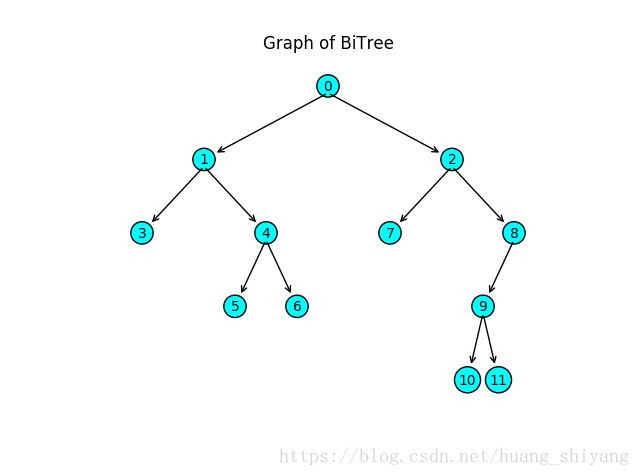
假设现在已经存在一颗二叉树,如下图2
新添加的结点按顺序做为结点2的左子结点(这里不考虑像二叉查找树等的插入要求)。基本插入方法如下:
判断根结点是否存在,如果不存在则插入根结点。否则从根结点开始,判断左子结点是否存在,如果不存在插入, 如果左子结点存在判断右结点,不存在插入。如果左右结点存在,再依次遍历左右子结点的子结点,直到插入成功。
上述的方法类似于层次遍历,体现了广度搜索优先的思想。因此从代码实现上,很显然需要一个队列对子结点进行入队与出队。在python上这很简单,一个list 就实现了,代码如下:
def add_node_in_order(self, element):
"""add a node to existent BiTree in order"""
node = BiNode(element)
if self.root is None:
self.root = node
else:
node_queue = list()
node_queue.append(self.root)
while len(node_queue):
q_node = node_queue.pop(0)
if q_node.left is None:
q_node.left = node
break
elif q_node.right is None:
q_node.right = node
break
else:
node_queue.append(q_node.left)
node_queue.append(q_node.right)
def set_up_in_order(self, elements_list):
"""set up BiTree from lists of elements in order """
for elements in elements_list:
self.add_node_in_order(elements)set_up_in_order()实现了通过列表对树进行顺序构造。
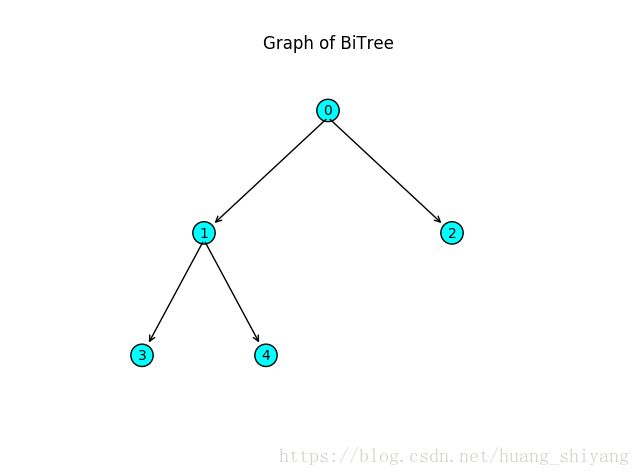
从字典初始化构造二叉树
当然你会发现,用上述方法构造的二叉树永远都是完全二叉树。实际情况下,我们需要初始化像图3这样的一棵不规则的二叉树,怎么办?

此时, 可以借住python的字典对树进行构造,参考的node的dict_form,约定”element”的key_value是结点值,“left”,“right”的key_value也是一个字典代表左右子树,如果为空则为None 。为方便书写,对于一个结点除了element不能缺外, 左右子树不存在时相应key可以缺失。同时对于叶结点,可以省略写成相应的元素值而不用继续构造一个字典。此时可以通过类似如下字典初始一棵二叉树表示,如下:
dict_tree = {
"element": 0,
"left": {
"element": 1,
"left": {
"element": 3,
"left": 6,
"right": 7,
}
},
"right": {
"element": 2,
"left": 4,
"right": {
"element": 5,
"left": 8,
"right": 9,
},
},
}上述字典表示的二叉树即为图3所示
通过字典进行初始树,可以借用层次遍历的思想实现树的构造,本质上其实就是对树进行一个非递归实现的拷贝,代码实现如下:
def set_up_from_dict(self, dict_instance):
"""set up BiTree from a dict_form tree using level traverse, or call it copy """
if not isinstance(dict_instance, dict):
return None
else:
dict_queue = list()
node_queue = list()
node = BiNode(dict_instance["element"])
self.root = node
node_queue.append(node)
dict_queue.append(dict_instance)
while len(dict_queue):
dict_in = dict_queue.pop(0)
node = node_queue.pop(0)
# in dict form, the leaf node might be irregular, like compressed to element type
# Thus , all this case should be solved out respectively
if isinstance(dict_in.get("left", None), (dict, int, float, str)):
if isinstance(dict_in.get("left", None), dict):
dict_queue.append(dict_in.get("left", None))
left_node = BiNode(dict_in.get("left", None)["element"])
node_queue.append(left_node)
else:
left_node = BiNode(dict_in.get("left", None))
node.left = left_node
if isinstance(dict_in.get("right", None), (dict, int, float, str)):
if isinstance(dict_in.get("right", None), dict):
dict_queue.append(dict_in.get("right", None))
right_node = BiNode(dict_in.get("right", None)["element"])
node_queue.append(right_node)
else:
right_node = BiNode(dict_in.get("right", None))
node.right = right_node
将二叉树打包成字典
往往我们也需要将一颗二叉树用字典的形式表示出来, 其方法与从字典初始化一棵二叉树一样,代码实现如下:
def pack_to_dict(self):
"""pack up BiTree to dict form using level traversal"""
if self.root is None:
return None
else:
node_queue = list()
dict_queue = list()
node_queue.append(self.root)
dict_pack = self.root.dict_form()
dict_queue.append(dict_pack)
while len(node_queue):
q_node = node_queue.pop(0)
dict_get = dict_queue.pop(0)
if q_node.left is not None:
node_queue.append(q_node.left)
dict_get["left"] = q_node.left.dict_form()
dict_queue.append(dict_get["left"])
if q_node.right is not None:
node_queue.append(q_node.right)
dict_get["right"] = q_node.right.dict_form()
dict_queue.append(dict_get["right"])
return dict_pack求二叉树的深度
求二叉树的深度或者高度的非递归实现,本质上可以通过层次遍历实现,方法如下:
1. 如果树为空,返回0 。
2. 从根结点开始,将根结点拉入列。
3. 当列非空,记当前队列元素数(上一层节点数)。将上层节点依次出队,如果左右结点存在,依次入队。直至上层节点出队完成,深度加一。继续第三步,直至队列完全为空。
代码实现如下:
def get_depth(self):
"""method of getting depth of BiTree"""
if self.root is None:
return 0
else:
node_queue = list()
node_queue.append(self.root)
depth = 0
while len(node_queue):
q_len = len(node_queue)
while q_len:
q_node = node_queue.pop(0)
q_len = q_len - 1
if q_node.left is not None:
node_queue.append(q_node.left)
if q_node.right is not None:
node_queue.append(q_node.right)
depth = depth + 1
return depth前序遍历
二叉树的前序,中序,后序称体现的是深度优先搜索的思想。
本质上它们的方法其实是一样的。
先说前序遍历, 方法如下:
1. 如果树为空,返回None 。
2. 从根结点开始,如果当前结点左子树存在,则打印结点,并将该结点入栈。让当前结点指向左子树,继续步骤2直至当前结点左子树不存在。
3. 将当结点打印出来,如果当前结点的右子树存在,当前结点指向右子树,继续步骤2。否则进行步骤4.
4. 如果栈为空则遍历结束。若非空,从栈里面pop一个节点,从当前结点指向该结点的右子树。如果右子树存在继续步骤2,不存在继续步骤4直至结束。
以图2为例,用N代表结点。
1.N0 ,N1依次打印,并且入栈。
2. 打印N3,
3. N3右子树不存在,N1出栈,遍历N1右子树N4
4. N4的左子树不存在,打印N4。N4右子树不存在,N0出栈,指向其右子树N2
5. N2的左子树不存在,打印N2,判断右子树及栈空结束
代码实现如下:
def pre_traversal(self):
"""method of traversing BiTree in pre-order"""
if self.root is None:
return None
else:
node_stack = list()
output_list = list()
node = self.root
while node is not None or len(node_stack):
# if node is None which means it comes from a leaf-node' right,
# pop the stack and get it's right node.
# continue the circulating like this
if node is None:
node = node_stack.pop().right
continue
# save the front node and go next when left node exists
while node.left is not None:
node_stack.append(node)
output_list.append(node.get_element())
node = node.left
output_list.append(node.get_element())
node = node.right
return output_list中序遍历
中序遍历的思想基本与前序遍历一样,只是最开始结点入栈时先不打印。只打印不存在左子树的当前结点,然后再出栈遍历右子树前再打印出来,代码实现如下:
def in_traversal(self):
"""method of traversing BiTree in in-order"""
if self.root is None:
return None
else:
node_stack = list()
output_list = list()
node = self.root
while node is not None or len(node_stack):
# if node is None which means it comes from a leaf-node' right,
# pop the stack and get it's right node.
# continue the circulating like this
if node is None:
node = node_stack.pop()
# in in-order traversal, when pop up a node from stack , save it
output_list.append(node.get_element())
node = node.right
continue
# go-next when left node exists
while node.left is not None:
node_stack.append(node)
node = node.left
# save the the last left node
output_list.append(node.get_element())
node = node.right
return output_list后序遍历
后序遍历的实现思想与前序、中序一样。有两种实现方式。
先说第一种,同中序遍历,只是中序时从栈中pop出一个结点打印,并访问当前结点的右子树。 后序必须在访问完右子树完在,在打印该结点。因此可先
看栈顶点是否被访问过,如果访问过,即已经之前已经做了其右子树的访问因此可出栈,并打印,继续访问栈顶点。如果未访问过,则对该点的访问标记置为访问,访问该点右子树。可以发现,相对于前序与中序,后序的思想是一致的,只是需要多一个存储空间来表示结点状态。python代码实现如下:
def post_traversal1(self):
"""method of traversing BiTree in in-order"""
if self.root is None:
return None
else:
node_stack = list()
output_list = list()
node = self.root
while node is not None or len(node_stack):
# if node is None which means it comes from a leaf-node' right,
# pop the stack and get it's right node.
# continue the circulating like this
if node is None:
visited = node_stack[-1]["visited"]
# in in-order traversal, when pop up a node from stack , save it
if visited:
output_list.append(node_stack[-1]["node"].get_element())
node_stack.pop(-1)
else:
node_stack[-1]["visited"] = True
node = node_stack[-1]["node"]
node = node.right
continue
# go-next when left node exists
while node.left is not None:
node_stack.append({"node": node, "visited": False})
node = node.left
# save the the last left node
output_list.append(node.get_element())
node = node.right
return output_list
另外,后续遍历还有一种访问方式。考虑到后续遍历是先左子树,再右子树再到父结点, 倒过来看就是先父结点, 再右子树再左子树。 是不是很熟悉, 是的这种遍历方式就是前序遍历的镜像试,除了改变左右子树访问顺序连方式都没变。 再将输出的结果倒序输出一遍就是后序遍历。 同样该方法也需要额外的空间存取输出结果。python代码如下:
def post_traversal2(self):
"""method of traversing BiTree in post-order"""
if self.root is None:
return None
else:
node_stack = list()
output_list = list()
node = self.root
while node is not None or len(node_stack):
# if node is None which means it comes from a leaf-node' left,
# pop the stack and get it's left node.
# continue the circulating like this
if node is None:
node = node_stack.pop().left
continue
while node.right is not None:
node_stack.append(node)
output_list.append(node.get_element())
node = node.right
output_list.append(node.get_element())
node = node.left
return output_list[::-1]求叶子节点
求叶子节点有两种方法,一种是广度搜索优先,即如果当前节点存在左右子树将左右子树入队。如果当前节点不存在子树,则该节点为叶节点。继续出队访问下一个节点。直至队列为空,这个方法留给读者去实现。
另外一种方法是,用深度搜索优先。 采用前序遍历,当判断到一个结点不存在左右子树时叶子结点数加一。代码实现如下:
def get_leaf_num(self):
"""method of getting leaf numbers of BiTree"""
if self.root is None:
return 0
else:
node_stack = list()
node = self.root
leaf_numbers = 0
# only node exists and stack is not empty that will do this circulation
while node is not None or len(node_stack):
if node is None:
"""node is None then pop the stack and get the node.right"""
node = node_stack.pop().right
continue
while node.left is not None:
node_stack.append(node)
node = node.left
# if there is not node.right, leaf_number add 1
node = node.right
if node is None:
leaf_numbers += 1
return leaf_numbers二叉树的可视化
到此, 除了树的结点删除(这个可以留给读者去尝试), 这里已经基本完成二叉树的构造及遍历接口。 但你可能真正在意的是如何绘制一颗二叉树。 接下来,本节将会通过python matplotlib.annotate绘制一颗二叉树。
要绘制一棵二叉树,首先需要对树中的任意结点给出相应相对坐标(axis_max: 1)。对于一棵已知树, 已知深度 d d ,那么可以设初始根结点坐标为 (1/2,1−12d) ( 1 / 2 , 1 − 1 2 d ) . (这个设置只是为了让根结点尽量中间往上且不触及axis)
假设已经知道父结点的坐标 (xp,yp) ( x p , y p ) , 当前层数 l l (记根节点为第0层),则从上往下画其左右子树的坐标表达如下:
左子树:
右子树:
对应代码实现如下:
def get_coord(coord_prt, depth_le, depth, child_type="left"):
if child_type == "left":
x_child = coord_prt[0] - 1 / (2 ** (depth_le + 1))
elif child_type == "right":
x_child = coord_prt[0] + 1 / (2 ** (depth_le + 1))
else:
raise Exception("No other child type")
y_child = coord_prt[1] - 1 / depth
return x_child, y_child如果知道当前结点与父结点坐标,即可以通过plt.annotate进行结点与箭标绘制,代码实现如下:
def plot_node(ax, node_text, center_point, parent_point):
ax.annotate(node_text, xy=parent_point, xycoords='axes fraction', xytext=center_point, textcoords='axes fraction',
va="bottom", ha="center", bbox=NODE_STYLE, arrowprops=ARROW_ARGS)已知树深度, 当前结点及当前结点所在层数,则可以通过上述计算方式计算左右子树的结点坐标。 使用层次遍历,即可遍历绘制整棵树。代码实现如下:
def view_in_graph(self):
"""use matplotlib.pypplot to help view the BiTree """
if self.root is None:
print("An Empty Tree, Nothing to plot")
else:
depth = self.get_depth()
ax = node_plot.draw_init()
coord0 = (1/2, 1 - 1/(2*depth))
node_queue = list()
coord_queue = list()
node_plot.plot_node(ax, str(self.root.get_element()), coord0, coord0)
node_queue.append(self.root)
coord_queue.append(coord0)
cur_level = 0
while len(node_queue):
q_len = len(node_queue)
while q_len:
q_node = node_queue.pop(0)
coord_prt = coord_queue.pop(0)
q_len = q_len - 1
if q_node.left is not None:
xc, yc = node_plot.get_coord(coord_prt, cur_level + 1, depth, "left")
element = str(q_node.left.get_element())
node_plot.plot_node(ax, element, (xc, yc), coord_prt)
node_queue.append(q_node.left)
coord_queue.append((xc, yc))
if q_node.right is not None:
xc, yc = node_plot.get_coord(coord_prt, cur_level + 1, depth, "right")
element = str(q_node.right.get_element())
node_plot.plot_node(ax, element, (xc, yc), coord_prt)
node_queue.append(q_node.right)
coord_queue.append((xc, yc))
cur_level += 1
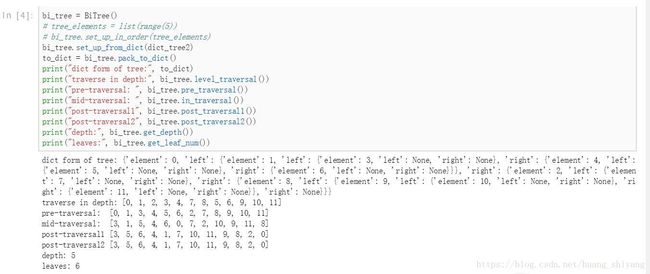
node_plot.show()最后, 可以对如下的一颗二叉树进行测试:
dict_tree2 = {
"element": 0,
"left": {
"element": 1,
"left": 3,
"right": {
"element": 4,
"left": 5,
"right": 6,
},
},
"right": {
"element": 2,
"left": 7,
"right": {
"element": 8,
"left": {
"element": 9,
"left": 10,
"right": 11,
},
},
},
}至此, 本文结。 Have fun reading , 需望此文可以帮助你了解二叉树的结构
如有疑惑请通过邮件联系:huangshiyang@[email protected]