这两天学习了一下红黑树,关于红黑树的资料如下,讲得很详细。
1. 教你透彻了解红黑树:
http://blog.csdn.net/v_JULY_v/archive/2010/12/29/6105630.aspx
2. 红黑树算法的层层剖析与逐步实现
http://blog.csdn.net/v_JULY_v/archive/2010/12/31/6109153.aspx
3. 教你彻底实现红黑树:红黑树的c源码实现与剖析
http://blog.csdn.net/v_JULY_v/archive/2011/01/03/6114226.aspx
4. 具体的插入和删除的例子:
http://saturnman.blog.163.com/blog/static/557611201097221570/
总结几点:
这里我们把当前节点的值改为其后继节点的值,那么真正删除的节点就是其后继节点。
1. 如果没有后继节点,那么这个节点就是真正要删除的节点。
2. 真正要删除的节点是红节点,就直接删除。
3. 真正删除的节点是红节点时,该红节点没有儿子,如果有的话,就要有两个黑儿子,该节点就不是真正要删除
的。
4. 真正删除的节点是黑节点时,该黑节点没有右儿子,可以有一个左红儿子,也可以没有儿子。
删除算法的根本思想是:
将实际需要删除黑节点记为v,该黑节点的父亲节点为pv。那么就需要调整pv,使得其左右子树的黑高度相同,但是这样pv这棵树的黑高度可能会降低,所以要继续向上调整。
我们称这个黑高度变低的子树的根节点为判定点吧,随便取的名字,只是好说而已。当判定点为红色时,直接将其变黑,结束。
实际删除节点为黑节点的几种类型:
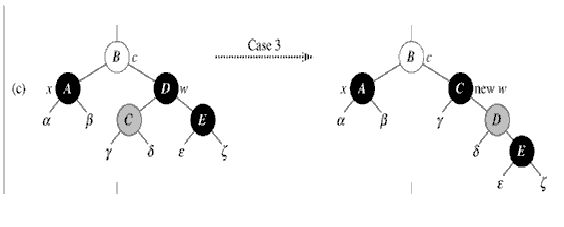
图中x标记的节点是判定点,表示以该节点为根的子树黑高度减小了1。
黑色为黑节点,灰色为红节点,白色为任意节点。而且图中都假设判定点在右子树上。
1. 红兄弟
(图片来自链接3)
2. 黑兄弟二黒侄。
(图片来自链接3)
3. 黑兄左红侄右黒侄
(图片来自链接3)
4. 黑兄右红侄
(图片来自链接3)
图中调整后,黑高度又相等了,所以不需要继续向上了。
总结几点;
红兄弟变黑兄弟,
兄侄全黑兄变红,判定点在右子树,
右黑侄变右红侄,判定点在左子树,左黑侄变左红侄。
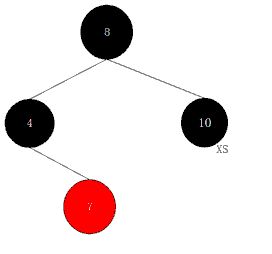
例1:
X标记要该节点要被删除,S标记以该节点为根的子树的黑高度变小了,S标记的点为判定点。
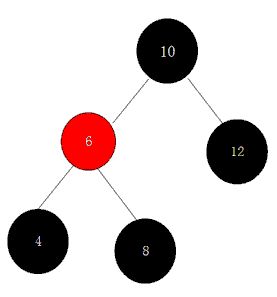
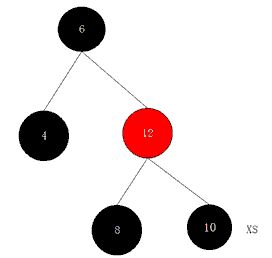
1. 删除节点10,则实际删除的是节点12
把10与12的值交换
第一步:红兄变黑兄(第1种情况)
第二歩:兄侄全黑兄变红(第2种情况)
此时,节点8没有儿子,相当于有两个黑儿子(黑哨兵)。
第三歩:判定节点为红色,直接将其变黑。将X点置为空。结束。
例2:删除节点3
第一步:兄侄全黑兄变红(第2种情况)
步骤二:红兄变黑兄(第1种情况)
第三步:兄侄全黑兄变红(第2种情况)
第四步:兄侄全黑兄变红(第2种情况)
将X点置为空,Over,已经平衡啦。
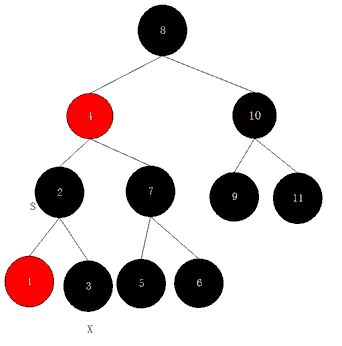
例3:
黑兄,左儿子为空,相当于左黑侄。
步骤一:判定点在右子树,左黑侄变左红侄。(第3种情况)
步骤二:判定点在右子树,有左红侄,第4种情况. Over了。
声明:不要轻信我写的哦~~自己推理一下~~如有不同,欢迎讨论。