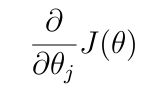机器学习之线性回归

这个系列是我学习coursera上《机器学习》课程的笔记，边学边练。上面有一些习题，课程要求用Octave（或Matlab）完成，但是这两个软件太强大，掩盖了很多细节，而且我写Octave代码的时候，总有种支离破碎的感觉，最后还是用C#去实现了，果然不适合当科学家，还是老老实实作码农吧。

界面使用WPF，我还自己写了个做图表的库，本来准备好好写写的，但是真的是太烦，特别是API的设计，因为是第一次设计，各种问题，自己用着都觉得翔气逼人。。不过作为演示还是可以的，勿喷。。。

一、线性回归

1.理论说明：

线性回归：Wiki上说：在统计学中，线性回归是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。

说白了，就是给你一大堆点，点由两个变量（先只考虑一元线性回归）决定；观察后，认为这两个变量应该是线性关系，于是就根据这堆点找出这个线性关系。

对于线性回归，有公式可以直接套，这里换种思路。

 

假设回归的函数为h(x) = a*x + b，这个是假设函数；回归的目的就是使假设函数靠谱，即对于测试数据（x1，y1），把x1代入假设函数，算出h(y1)，然后h(x1)和y1越接近越好，两者的差距可以用( h(x1) - y1 )²来衡量。对于所有测试数据，就是求个和：

                             

这个求和的式子就是一元线性回归的cost function（不知要怎么翻译），θ代指参数(这里是θ₀是a，θ₁是b)，cost函数是与参数有关的函数，和x、y无关（这话要好好理解一下）。前面的1/2是为了以后求导方便，对结果没有影响（也可以接着除以测试数据的个数m，即前面的系数为1/2m）；上标i表示第i个测试数据。cost函数表征了假设的函数与实际数据的偏差。要使偏差最小，问题最终转化为最小化cost函数。

看到这里，如果你高中数学学得还不错，应该能说一句：我艹，不就是令导数等于0吗！但是，这一句话，要转换成程序就不是很容易了。计算机最擅长迭代，可以换种思路：

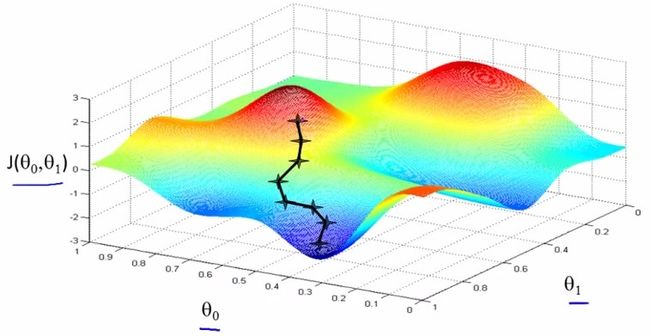
打个比方，你从山上下去，你也不知道怎么走最好，环顾四周发现，左斜45度下去的方向下降的最快。好，走一步；然后从新环顾四周，发现直走一步，下去的最多，好，走一步。一直重复这个过程，直到你发现，四周海拔都比你高。如下图所示。

首先要解决的就是，这个方向怎么确定。针对这张图，这个方向是由θ₀和θ₁共同确定的。沿θ₀方向走一定长度，沿θ₁方向走一定长度，两个向量相加，就确定了要下降的方向，即确定两个向量的长度比例即可。

实际上，这个方向是梯度的负方向。梯度方向，是函数上升最快的方向，那么负梯度方向当然就是下降最快的方向。关于梯度的推导和性质，可以参考高等数学的相关内容(记得是同济版高数书下册的空间几何相关章节，不确定)。这里直接给出其形式：

 

J对θ₀求偏导，得到沿θ₀方向前进的距离；J对θ₁求偏导，得到沿θ₁方向前进的距离；保持两个向量的比例，即确定了下一步的前进方向。

对于h=a* x + b的情况，假设这一步需要沿a方向走d(a)距离，沿b方向走的d(b)距离，那么在一次迭代中，只要下式同步更新a和b的值，那么这次迭代后，J函数就沿下降最快的方向，走了一步

a := a + α * d(a)

 b: = b +α* d(b)

对于步长α，总的来说就是不能太大，也不要太少。有没有一种自然辨证法的感觉（⊙﹏⊙|汗）。想象一个二次曲线，如果步子太大，会直接把最低点夸过去，而且步子大了，还有可能扯着那啥；步子太小，收敛太慢。步长一般不是常数，是一个函数，就是说随着迭代的进行，它的值会变化。

迭代公式的思想其实很简单，就是：

下一个值 =当前值 +步长 *方向

这个式子可以高度概括最优化这门课一半以上的内容，有这个式子，这门课就可以及格了~ ~。

 

 二：把数学公式写成程序的形式

数学公式太难输入，下面用写程序的方式对公式进行表示，请大家熟悉以下表述方法（对于24K纯屌丝码农，应该挺适应这种方式的~~）：

把J写成代码形式：

J = 1/2 * sum ( powOf2(h-y)  ) ;

用Pd(J)来表示求偏导函数。按照这种方式，迭代公式可以写成如下形式：

θ := θ – step() * Pd(J)

 

三、迭代公式推导：

下面针对h=a * x + b的情况进行偏导计算，如果对推导过程不感兴趣，可以直接看下面的推导结果。不过，还是建议大家拿笔推一下。

首先对参数a进行求偏导：

Cost函数J对a求偏导：

Pda(J)  = sum(  ( h-y )*Pd(h-y)  )//链式求导法则

Pda(J)  = sum(  (a*x+b-y) * Pd(a*x-+b-y) ) //把h=a * x + b代入

Pda(J)  =  sum( (a*x+b-y) * x  )//  a*x+b-y对a求偏导后，得x

 

对b求偏导

Pdb(J) =sum(  (a*x+b-y)*1 ) //可以认为b是 x0项的系数，x0是常数，等于1

写成数学式子，就是：

                             

四、推导结果：

如果对推导不感兴趣，直接看迭代的式子吧：

a := a – α * (a*x+b-y ) * x

b := b - α*  (a*x+b-y )

    有这个结果后，就可以写程序啦。

一头雾水吗？这说明，你还比较正常~~。现在你需要记住迭代公式的思想

下一个值 =当前值 +步长 *方向

下面通过代码来演示这一过程。

五、准备数据

下面实际上，就是完成Coursera上课程的编程练习1。具体信息大家可以去www.coursera.org 上去看。

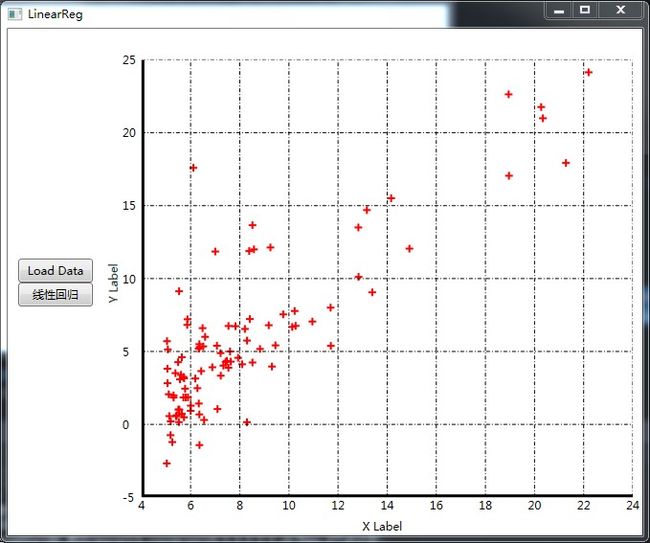
ex1data1.txt中为需要回归的数据，每一行2个数，以英文逗号分割。

 

  private void Button_Click_LoadData(object sender, RoutedEventArgs e)
        {
	    //点击load data按钮，装载数据
            LoadData(@"ex1data1.txt");//把ex1data1.txt直接放在Debug或Release目录下
        }

         private void LoadData(String fileName)
        {
            
            StreamReader sr = new StreamReader(fileName);
            String line = null;
            while((line = sr.ReadLine())!=null)
            {
                data.Add(ConvertToPoint2D(line.Split(',')));
            }
            sr.Close();
            //…后面是画图的部分，没有使用第三方控件，自己写的画图库，但是写的翔气熏天，大家看看知道干嘛就好，别深究，求大神轻虐
        }
	//ConvertToPoint2D函数就是把长度是2的字符串数组，转成point
	private Point ConvertToPoint2D(String[] ss)
        {
            if(ss.Length!=2)
                throw new ArgumentException("parameter should contains two string");
            return new Point(){X = Convert.ToDouble(ss[0]),Y=Convert.ToDouble(ss[1])};
        } 

 

结果见图

 

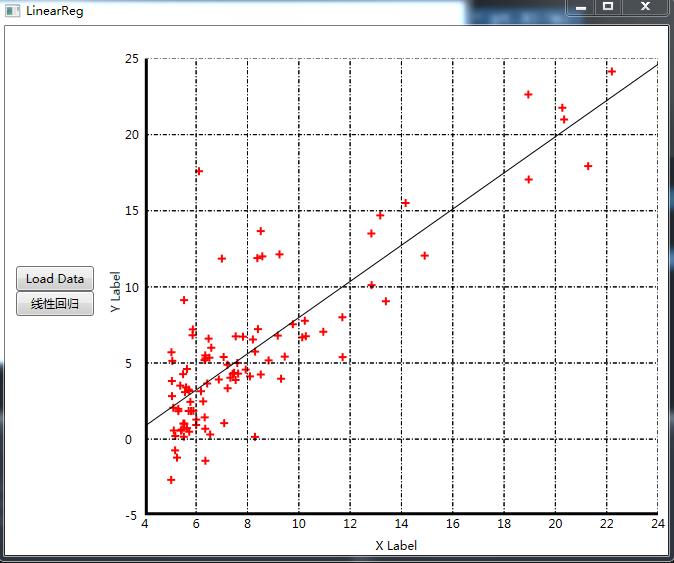
点击“线性回归”按钮后，得到结果，图和代码见下面：

 

        private void Button_Click(object sender, RoutedEventArgs e)
        {
            //h : a*x+b
            //cost function J : 1/2 * sum( Pow(a*x+b-y,2) )
            //J 对 a的偏导为 sum((a*x+b-y)*x)
            //J 对 a的偏导为 sum((a*x+b-y)*x)
            //
            //a := a - 0.01 * sum((a*x+b-y)*x)
            //b := b - 0.01 * sum((a*x+b-y))

            //a,b初始为0
            double a = 0;
            double b = 0;
            double m = data.Count;

            //StreamWriter sw =new StreamWriter(@"E:\result4.txt");
            List cost =new List();
            double d1 = 0, d2 = 0;
            double d3 = 0;
            /*判定停止的条件：
            1.cost function的值，变化足够小
            2.各个参数的值，变化均足够小
            3.迭代一定次数（这里简单的使用这一方法）
            4.whatever
            */
            for(int i=0;i<10000;i++)
            {

                d1 = data.Sum(pt => (a * pt.X + b - pt.Y) * pt.X)/m;
                d2 = data.Sum(pt => a * pt.X + b - pt.Y)/m;
                d3 = Math.Sqrt(d1 * d1 + d2 * d2);//用于把方向变成单位向量
  
                a = a -   0.01*d1 / d3;//步长定为0.01，实际上应该是个函数，这里进行了简化
                b = b -  0.01*d2 / d3;//步长的大小需要一样，以保证方向
                //a = a -  d1 / d3/(i+1);
                //b = b -  d2 / d3/(i+1);
                //把a，b和cost输出为文件
                //sw.WriteLine(String.Format("{0},{1},{2}",a,b,data.Sum(pt=>Math.Pow(a*pt.X+b-pt.Y,2))));
            }
            //sw.Close();
            List twoPoints = new List() { new Point(4, a * 4 + b), new Point(24, a * 24 + b) };
            LineSeries ls = new LineSeries();
            ls.ItemSource = twoPoints;
            this.chart.AddSeries(ls);
            this.chart.UpdateChart();
        }

总结一下回归步骤吧，这个流程很重要：

1. 找到假设函数H

2.找到合适的Cost函数J

3 最小化函数J，按照下面的思路：

        下一个值 =当前值 +步长 *方向

        如何定步长和方向是关键，可能需要不断的尝试

4.写程序，调试

 

下一节练习Logistic回归，本节Over。