【3.搜索算法——编程题】
目录
1.简单题目
1.1平衡二叉树(深度优先搜索)
1.2对称二叉树(广度优先搜索)
1.3只出现一次的数字(哈希)
1.4相同的树(深度优先搜索)
1.5 二叉树的最大深度(深度优先搜索)
1.6腐烂的橘子(广度优先搜索)
1.7最长回文串(哈希)
2.中等题目
2.1组合总和(回溯算法)
2.2组合总和Ⅱ(回溯算法)
2.3全排列(回溯算法)
2.4全排列问题Ⅱ(回溯算法)
2.5有效的数独(哈希)
2.6特殊回文数(回溯)
2.8 零钱兑换(bfs + 剪枝)
2.9岛屿的最大面积(深度/广度优先遍历)
2.10被围绕的区域(深度优先搜索)
2.11岛屿数量(深度优先搜索)
2.12 砖墙(哈希)
3.困难题目
3.1N皇后问题(回溯算法)
1.简单题目
1.1平衡二叉树(深度优先搜索)
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
示例 1:
给定二叉树 [3,9,20,null,null,15,7]
3
/ \
9 20
/ \
15 7
返回 true 。
示例 2:
给定二叉树 [1,2,2,3,3,null,null,4,4]
1
/ \
2 2
/ \
3 3
/ \
4 4
返回 false 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/balanced-binary-tree
暂时没有更好的方法,只能用深度搜索各个节点(深度优先搜索,递归),如果某个节点的左子树高度 - 右子树高度的绝对值 > 1(递归),则直接返回false。当遍历完之后,栈为空则认为该树是平衡二叉树,返回true。
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
stack stack1;
int height(TreeNode* t){
/*
* 求该节点高度
*/
if(t == nullptr)
return 0;
else{
int hl = height(t->left);
int hr = height(t->right);
if(hl >= hr)
return 1 + hl;
else
return 1 + hr;
}
}
bool dfs(TreeNode* t){
/*
* 深度优先搜索该树
*/
stack1.pop();
if(t != nullptr && (t->left != nullptr || t->right != nullptr)){
if(abs(height(t->left) - height(t->right)) > 1)
return false;
}
if(t != nullptr){
if(t->right != nullptr)
stack1.push(t->right);
if(t->left != nullptr)
stack1.push(t->left);
}
if(stack1.empty())
return true;
else{
return dfs(stack1.top());
}
}
bool isBalanced(TreeNode* root) {
stack1.push(root);
return dfs(root);
} 执行用时 :12 ms, 在所有 C++ 提交中击败了92.11%的用户
内存消耗 :16.9 MB, 在所有 C++ 提交中击败了86.03%的用户
1.2对称二叉树(广度优先搜索)
给定一个二叉树,检查它是否是镜像对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/ \
2 2
/ \ / \
3 4 4 3
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1
/ \
2 2
\ \
3 3
说明:
如果你可以运用递归和迭代两种方法解决这个问题,会很加分。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/symmetric-tree
方法1:二叉树类的题目因为有规律可循,可用分治法,很多用递归即可(画个三层的二叉树,就能把下面的关系搞清楚了)
queue queue1;
bool fun(TreeNode* left, TreeNode* right){
if(left == nullptr && right == nullptr){
return true;
}
if(left != nullptr && right != nullptr){
if(left->val == right->val && fun(left->left, right->right)
&& fun(left->right, right->left))
return true;
}
return false;
}
//递归方法
bool isSymmetric(TreeNode* root){
if(root != nullptr)
return fun(root->left, root->right);
return true;
} 方法2:用层次遍历(广度优先搜索),用一个vector保存每一层的元素,判断每一层是否是回文数。
bool judge(vector vals){
//判断是否回文数
for(int i = 0, j = vals.size() - 1; i < j; i++, j--){
if(vals[i] != vals[j])
return false;
}
return true;
}
bool isSymmetric(TreeNode* root){
if(root == nullptr)
return true;
if(root->left == nullptr && root->right == nullptr)
return true;
vector vals;
queue1.push(root);
int count = 0;
int flag = 1;
while(!queue1.empty()){
TreeNode *t = queue1.front();
if(t == nullptr)
vals.push_back(-1); //null节点视为-1
else
vals.push_back(t->val);
count++;
queue1.pop();
if(t != nullptr){
queue1.push(t->left);
queue1.push(t->right);
}
//一层结束
if(count == flag){
flag = queue1.size(); //下一层有多少节点
count = 0;
if(!judge(vals))
return false;
vals.clear();
}
}
return true;
} 1.3只出现一次的数字(哈希)
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
输入: [2,2,1]
输出: 1
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/single-number
用哈希表的方法解题很方便,只是使用了额外空间,每个元素值对应一个key。当我们向哈希集添加重复元素时,如果添加失败,则移除当前试图向哈希集添加的元素。
int singleNumber(vector& nums) {
map map1;
for (int &num : nums) {
if(map1.find(num) != map1.end())
map1.erase(num);
else
map1.insert(map::value_type(num, num));
}
auto iter = map1.begin();
return iter->first;
} 1.4相同的树(深度优先搜索)
给定两个二叉树,编写一个函数来检验它们是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
输入: 1 1
/ \ / \
2 3 2 3
输出: true
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/same-tree
递归方法(深度优先搜索)返回条件:
- 两节点都空,return true
- 其中一个为空,return false
- 值不同,return false
bool isSameTree(TreeNode* p, TreeNode* q){
if(!p && !q)
return true;
if(p == nullptr || q == nullptr)
return false;
if(p->val != q->val)
return false;
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}自己写了一个用栈进行深度遍历的解法,本质一样的,在遍历过程中出现以下情况返回false:
- 一空一不空
- 值不同
- 一栈空一栈不空
stack stackp, stackq;
bool dfs(TreeNode* p, TreeNode* q){
stackp.pop();
stackq.pop();
if(p || q){
if(p != nullptr && q != nullptr){
if(p->val != q->val)
return false;
stackp.push(p->left);
stackp.push(p->right);
stackq.push(q->left);
stackq.push(q->right);
} else{
return false;
}
}
if(stackp.empty() && stackq.empty())
return true;
else{
if(!stackp.empty() && !stackq.empty())
return dfs(stackp.top(), stackq.top());
else
return false;
}
}
bool isSameTree(TreeNode* p, TreeNode* q) {
stackp.push(p);
stackq.push(q);
return dfs(p, q);
} 1.5 二叉树的最大深度(深度优先搜索)
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
就是求二叉树的高度
int maxDepth(TreeNode* root) {
if(root == nullptr)
return 0;
else{
int hl = maxDepth(root->left);
int hr = maxDepth(root->right);
if(hl >= hr)
return hl + 1;
else
return hr + 1;
}
}1.6腐烂的橘子(广度优先搜索)
在给定的网格中,每个单元格可以有以下三个值之一:
值 0 代表空单元格;
值 1 代表新鲜橘子;
值 2 代表腐烂的橘子。
每分钟,任何与腐烂的橘子(在 4 个正方向上)相邻的新鲜橘子都会腐烂。
返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/rotting-oranges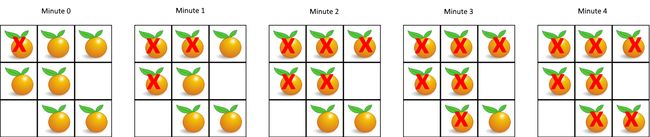
运用多源广度优先搜索,先把初试腐烂的橘子位置加入到队列,然后进行广度优先遍历。求腐烂的时间,即求遍历的层数。
详见https://leetcode-cn.com/problems/rotting-oranges/solution/fu-lan-de-ju-zi-by-leetcode-solution/
int orangesRotting(vector>& grid) {
vector > direction = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};//上下左右
int time = 0; // time实际为广度优先遍历的层数 - 1(因为最后一层橙子不需要计算)
int freshOreNum = 0; //新鲜橙子数量
queue > que;
int row = grid.size();
int col = grid[0].size();
bool visited[row][col];
for (int i = 0; i < row; ++i) {
for (int j = 0; j < col; ++j) {
visited[i][j] = false;
}
}
for (int i = 0; i < row; ++i) {
for (int j = 0; j < col; ++j) {
if(grid[i][j] == 2){
que.push(make_pair(i, j));
} else if(grid[i][j] == 1){
freshOreNum++;
}
}
}
if(freshOreNum == 0)//本身就没有新鲜橙子,就直接返回
return 0;
int flag = que.size(); //存储下一层数量
int count = 0;
while (!que.empty()){
pair org = que.front();
que.pop();
count++;
for(int i = 0; i < 4; i++){ //上下左右四个方向
int adji = org.first + direction[i][0];
int adjj = org.second + direction[i][1];
if(adji >= 0 && adji < row && adjj >= 0 && adjj < col){ //是否越界
if(!visited[adji][adjj] && grid[adji][adjj] == 1){ //未访问且是新鲜橙子
visited[adji][adjj] = true;
que.push(make_pair(adji, adjj));
freshOreNum--;
}
}
}
if(count == flag){//遍历完一层,time++
flag = que.size();
time++;
count = 0;
}
}
return freshOreNum == 0 ? time - 1 : -1;
} 1.7最长回文串(哈希)
给定一个包含大写字母和小写字母的字符串,找到通过这些字母构造成的最长的回文串。
在构造过程中,请注意区分大小写。比如 "Aa" 不能当做一个回文字符串
输入:
"abccccdd"
输出:
7
int longestPalindrome(string s) {
map map1;
for(int i = 0; i < s.length(); i++){
if(map1.find(s[i]) == map1.end()){
map1.insert(make_pair(s[i], 1));
} else{
map1[s[i]]++;
}
}
int res = 0;
auto iter = map1.begin();
int flag = 0;
for (iter; iter != map1.end(); iter++) {
if(iter->second % 2 == 0){
res += iter->second;
} else{
res += iter->second - 1;
flag = 1;
}
}
if(flag)
res += 1;
return res;
} 2.中等题目
2.1组合总和(回溯算法)
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
所有数字(包括 target)都是正整数。
解集不能包含重复的组合。
示例 1:
输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/combination-sum
本身就没有重复数字,所以也没必要用set容器。
先将数组排序,因为它没有重复元素,所以直接用回溯法即可。每一次回溯将target - candidates[i]作为参数传递,当 target - candidate[i] == 0 时,则认为当前序列是可行解,加入到解空间。traceback函数中 i 指针将不从0开始遍历,而是直接从上一层 i 指针开始(前提是已经排序)。
void traceback(vector &candidates, int target, vector> &res, vector &temp, int begin){
if(target <= 0){
if(target == 0)
res.push_back(temp);
return;
}
for(int i = begin; i < candidates.size(); i++){
temp.push_back(candidates[i]);
traceback(candidates, target - candidates[i], res, temp, i);
temp.pop_back();
}
}
vector> combinationSum(vector& candidates, int target) {
vector> res = {};
vector temp = {};
sort(candidates.begin(), candidates.end());
traceback(candidates, target, res, temp, 0);
return res;
} 2.2组合总和Ⅱ(回溯算法)
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明:
所有数字(包括目标数)都是正整数。
解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/combination-sum-ii
较上题不同的是:1、每个数字在每个组合中只能出现一次(例子中的1,1属于不同的数字,只是数值相等)。
2、candidates 有重复数字
说明:1、下次调用回溯函数只能传参 i + 1,作为for循环的begin
2、同一层for循环中,有重复的数字就跳过,不同层的就不用考虑(把回溯算法考虑为n个for循环),这样就能避免取值重复。
补充:
- 例如[1, 7],1属于第一层,7属于第二层
void traceback2(vector &candidates, int target, vector> &res, vector &temp, int begin, int dep){
if(target <= 0){
if(target == 0)
res.push_back(temp);
return;
}
for(int i = begin; i < candidates.size(); i++){
if(i > begin){ //在同一层for循环中,有重复的则跳过,不同层的不用考虑
if(candidates[i] == candidates[i - 1]){
continue;
}
}
temp.push_back(candidates[i]);
traceback2(candidates, target - candidates[i], res, temp, i + 1, dep + 1);
temp.pop_back();
}
}
vector> combinationSum2(vector& candidates, int target) {
vector> res = {};
vector temp = {};
sort(candidates.begin(), candidates.end());
traceback2(candidates, target, res, temp, 0, 0);
return res;
} 还有一个办法:既然去重,很容易想到set容器,用set容器就不需要考虑去重条件(有时候去重条件不是很容易想到),但是要承受执行用时。
void traceback3(vector &candidates, int target, set> &res, vector &temp, int begin) {
if(target <= 0){
if(target == 0)
res.insert(temp);
return;
}
for(int i = begin; i < candidates.size(); i++){
temp.push_back(candidates[i]);
traceback3(candidates, target - candidates[i], res, temp, i + 1);
temp.pop_back();
}
}
vector> combinationSum3(vector& candidates, int target){
vector> res = {};
set> set1;
vector temp = {};
sort(candidates.begin(), candidates.end());
traceback3(candidates, target, set1, temp, 0);
res.assign(set1.begin(), set1.end());
return res;
} 2.3全排列(回溯算法)
给定一个没有重复数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/permutations
一道经典的回溯算法,直接进模板即可。加入解的判断条件是当前解还未存在该元素。
bool exist(vector &temp, int num){
for (int i : temp) {
if(i == num)
return true;
}
return false;
}
void traceback(vector nums, vector> &res, vector &temp, int dep){
if(dep == nums.size()){
res.push_back(temp);
return;
}
for(int i = 0; i < nums.size(); i++){
if(!exist(temp, nums[i])){
temp.push_back(nums[i]);
traceback(nums, res, temp, dep + 1);
temp.pop_back();
}
}
}
vector> permute(vector& nums) {
sort(nums.begin(), nums.end());
vector> res;
vector temp;
traceback(nums, res, temp, 0);
return res;
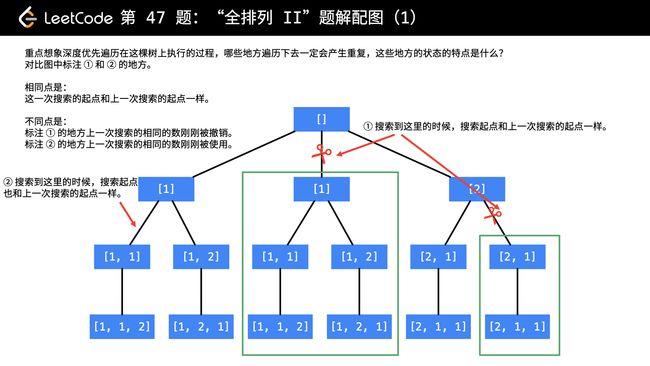
} 2.4全排列问题Ⅱ(回溯算法)
给定一个可包含重复数字的序列,返回所有不重复的全排列。
示例:
输入: [1,1,2]
输出:
[
[1,1,2],
[1,2,1],
[2,1,1]
]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/permutations-ii
与上题不同的是所给的序列中包含重复数字,所以要考虑去重问题。另外,上题解法中的exist()函数也不能使用了,转而用used[]数组来判断是否可以将该数字加入解,进而去重(剪枝)。(或者就直接用set暴力去解)
void traceback2(vector nums, vector> &res, vector &temp, vector &used, int dep){
if(dep == nums.size()){
res.push_back(temp);
return;
}
for(int i = 0; i < nums.size(); i++){
if(!used[i]){
if(i > 0){
if(nums[i] == nums[i - 1] && !used[i - 1])
continue;
}
used[i] = true;
temp.push_back(nums[i]);
traceback2(nums, res, temp, used, dep + 1);
temp.pop_back();
used[i] = false;
}
}
}
vector> permuteUnique(vector& nums){
sort(nums.begin(), nums.end());
vector> res;
vector temp;
vector used(nums.size());
used = {false};
traceback2(nums, res, temp, used, 0);
return res;
} 下图摘自力扣
2.5有效的数独(哈希)
判断一个 9x9 的数独是否有效。只需要根据以下规则,验证已经填入的数字是否有效即可。
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
![]()
上图是一个部分填充的有效的数独。
数独部分空格内已填入了数字,空白格用 '.' 表示。
示例 1:
输入:
[
["5","3",".",".","7",".",".",".","."],
["6",".",".","1","9","5",".",".","."],
[".","9","8",".",".",".",".","6","."],
["8",".",".",".","6",".",".",".","3"],
["4",".",".","8",".","3",".",".","1"],
["7",".",".",".","2",".",".",".","6"],
[".","6",".",".",".",".","2","8","."],
[".",".",".","4","1","9",".",".","5"],
[".",".",".",".","8",".",".","7","9"]
]
输出: true
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/valid-sudoku
新建map消耗内存的方法:创建三个map
bool exist(vector &temp, char ch){
for(int i = 0; i < temp.size(); i++){
if(temp[i] == ch)
return true;
}
return false;
}
bool isValidSudoku(vector>& board) {
map> row;
map> col;
map> section;
for(int i = 0; i < board.size(); i++){
for(int j = 0; j < board[i].size(); j++){
if(board[i][j] != '.'){
row[i].push_back(board[i][j]);
col[j].push_back(board[i][j]);
section[(i / 3) * 3 + j / 3].push_back(board[i][j]);
}
}
}
for(int i = 0; i < 9; i++){
vector temp;
for(int j = 0; j < row[i].size(); j++){
if(!exist(temp, row[i][j]))
temp.push_back(row[i][j]);
else
return false;
}
temp.clear();
for(int j = 0; j < col[i].size(); j++){
if(!exist(temp, col[i][j]))
temp.push_back(col[i][j]);
else
return false;
}
temp.clear();
for(int j = 0; j < section[i].size(); j++){
if(!exist(temp, section[i][j]))
temp.push_back(section[i][j]);
else
return false;
}
}
return true;
} 2.6特殊回文数(回溯)
摘自蓝桥杯
问题描述
123321是一个非常特殊的数,它从左边读和从右边读是一样的。
输入一个正整数n, 编程求所有这样的五位和六位十进制数,满足各位数字之和等于n 。
输入格式
输入一行,包含一个正整数n。
输出格式
按从小到大的顺序输出满足条件的整数,每个整数占一行。
样例输入
52
样例输出
899998
989989
998899
void traceback(vector > &nums, vector &temp, int target){
if(!temp.empty()){
if(temp.front() == 0)
return;
}
if(temp.size() == 3){
int count = 0;
for(int j = 0; j < 2; j++){
count += temp[j];
}
if((count + temp[2]) * 2 == target){ //符合6数
for (int j = 2; j >= 0; j--) {
temp.push_back(temp[j]);
}
nums.push_back(temp);
for (int j = 2; j >= 0; j--) { //还原temp
temp.pop_back();
}
}
if(count * 2 + temp[2] == target){//符合5数
for (int j = 1; j >= 0; j--) {
temp.push_back(temp[j]);
}
nums.push_back(temp);
for (int j = 1; j >= 0; j--) {//还原temp
temp.pop_back();
}
}
return;
}
for (int i = 0; i < 10; i++) {
temp.push_back(i);
traceback(nums, temp, target);
temp.pop_back();
}
}
int main(){
vector > res;
vector temp;
vector resNum;
int input;
cin >> input;
traceback(res, temp, input);
//sort(res.begin(), res.end());
for(int i = 0; i < res.size(); i++){
int flag = 1, count = 0;
for(int j = res[i].size() - 1; j >= 0; j--){
count += res[i][j] * flag;
flag *= 10;
}
resNum.push_back(count);
}
sort(resNum.begin(), resNum.end());
for (int i = 0; i < resNum.size(); i++) {
if(i == resNum.size() - 1)
cout << resNum[i];
else
cout << resNum[i] << endl;
}
} 2.8 零钱兑换(bfs + 剪枝)
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
示例 1:
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/coin-change
bfs + 剪枝的效果要比DP好。当前硬币count+之后最少的硬币数量>=目前结果,就剪枝
void dfs(vector& coins, int amount, int begin, int& ans, int count){
if(amount < 0)
return;
int coin = coins[begin];
if(begin < 0)
return;
if(amount % coin == 0){ //满足整数约束
ans = min(ans, amount / coin + count);
} else{
for(int i = amount / coin; i >= 0; i--){
if(count + i >= ans) //剪枝条件,当前count+之后最少硬币数量>=目前结果
break; //注意这里不能是continue,否则会超时
dfs(coins, amount - coin * i, begin - 1, ans, count + i);
}
}
}
int coinChange(vector& coins, int amount) {
sort(coins.begin(), coins.end());//排序
int ans = amount + 1;//初始最少硬币数量
dfs(coins, amount, coins.size() - 1, ans, 0);
return ans == amount + 1 ? -1 : ans;
} 2.9岛屿的最大面积(深度/广度优先遍历)
给定一个包含了一些 0 和 1的非空二维数组 grid , 一个 岛屿 是由四个方向 (水平或垂直) 的 1 (代表土地) 构成的组合。你可以假设二维矩阵的四个边缘都被水包围着。
找到给定的二维数组中最大的岛屿面积。(如果没有岛屿,则返回面积为0。)
示例 1:
[[0,0,1,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],
[0,1,0,0,1,1,0,0,1,0,1,0,0],
[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,0,1,1,0,0,0,0]]
对于上面这个给定矩阵应返回 6。注意答案不应该是11,因为岛屿只能包含水平或垂直的四个方向的‘1’。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/max-area-of-island
我采用的是广度优先搜索,使用队列辅助。我们只访问值为1的元素,每当访问过一个元素时,就将该元素置0,意义跟visited相同。
vector > dir = {{-1,1,0,0}, {0,0,-1,1}};
int dfs(vector>& grid, int i, int j){
int ans = 0;
queue> que;
que.push(make_pair(i, j));
grid[i][j] = 0; // 访问了就置0
while (!que.empty()){
pair tmp = que.front();
que.pop();
ans++;
for(int k = 0; k < 4; k++){
int next_i = tmp.first + dir[0][k];
int next_j = tmp.second + dir[1][k];
if(next_i >= 0 && next_i < grid.size() && next_j >= 0 &&
next_j < grid[0].size() && grid[next_i][next_j] == 1){
grid[next_i][next_j] = 0;
que.push(make_pair(next_i, next_j));
}
}
}
return ans;
}
int maxAreaOfIsland(vector>& grid) {
int maxArea = 0;
for(int i = 0; i < grid.size(); i++){
for (int j = 0; j < grid[0].size(); j++) {
if(grid[i][j] == 1){
maxArea = max(maxArea, dfs(grid, i, j));
}
}
}
return maxArea;
} 2.10被围绕的区域(深度优先搜索)
给定一个二维的矩阵,包含 'X' 和 'O'(字母 O)。
找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。
示例:
X X X X
X O O X
X X O X
X O X X
运行你的函数后,矩阵变为:
X X X X
X X X X
X X X X
X O X X
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/surrounded-regions
换种思路,将区域里所有的 'O' 用 'X' 填充,可以先把与边界处O的O标记(深度优先遍历,将与边界处相连的O都换成#),然后再把所有O改成#.
vector > dir = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
void dfs(vector>& board, int i, int j){
int row = board.size();
int col = board[0].size();
board[i][j] = '#';
for(int k = 0; k < 4; k++){
int new_i = i + dir[k][0];
int new_j = j + dir[k][1];
if(new_i >= 0 && new_i <= row - 1 && new_j >= 0 && new_j <= col - 1
&& board[new_i][new_j] == 'O'){
dfs(board, new_i, new_j);
}
}
}
void solve(vector>& board) {
if(board.empty())
return;
int row = board.size();
int col = board[0].size();
//先对边界处O检测,凡是与边界连通均赋值为#
for (int i = 0; i < row; ++i) {
for (int j = 0; j < col; ++j) {
if(i == 0 || j ==0 || i == row - 1 || j == col - 1){
if(board[i][j] == 'O'){
dfs(board, i, j);
}
}
}
}
//将内部的O变为X
for (int i = 0; i < row; ++i) {
for (int j = 0; j < col; ++j) {
if(board[i][j] == 'O'){
board[i][j] = 'X';
} else if(board[i][j] == '#'){
board[i][j] = 'O';
}
}
}
} 2.11岛屿数量(深度优先搜索)
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:
11110
11010
11000
00000
输出: 1
示例 2:
输入:
11000
11000
00100
00011
输出: 3
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/number-of-islands
边深度遍历边修改、计数就可
vector > dir = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
void dfs(vector>& grid, int i, int j){
int row = grid.size();
int col = grid[0].size();
grid[i][j] = '#';
for(int k = 0; k < 4; k++){
int new_i = i + dir[k][0];
int new_j = j + dir[k][1];
if(new_i >= 0 && new_i <= row - 1 && new_j >= 0 && new_j <= col - 1
&& grid[new_i][new_j] == '1'){
dfs(grid, new_i, new_j);
}
}
}
int numIslands(vector>& grid) {
if(grid.empty())
return 0;
int row = grid.size();
int col = grid[0].size();
int count = 0; // 计数
for (int i = 0; i < row; ++i) {
for (int j = 0; j < col; ++j) {
if(grid[i][j] == '1'){
count++;
dfs(grid, i, j); // 凡是相连就改为'#'
}
}
}
return count;
} 2.12 砖墙(哈希)
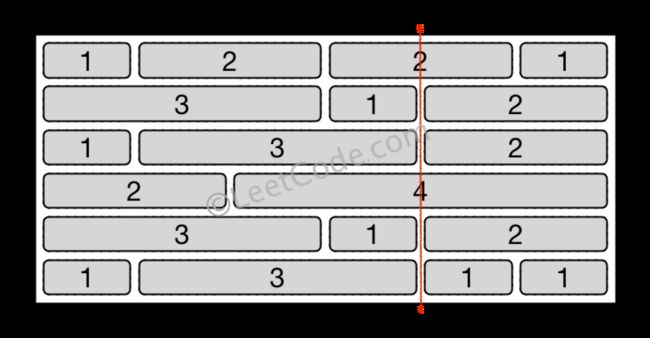
你的面前有一堵方形的、由多行砖块组成的砖墙。 这些砖块高度相同但是宽度不同。你现在要画一条自顶向下的、穿过最少砖块的垂线。
砖墙由行的列表表示。 每一行都是一个代表从左至右每块砖的宽度的整数列表。
如果你画的线只是从砖块的边缘经过,就不算穿过这块砖。你需要找出怎样画才能使这条线穿过的砖块数量最少,并且返回穿过的砖块数量。
你不能沿着墙的两个垂直边缘之一画线,这样显然是没有穿过一块砖的。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/brick-wall
输入: [[1,2,2,1],
[3,1,2],
[1,3,2],
[2,4],
[3,1,2],
[1,3,1,1]]
输出: 2
翻译:穿过砖最少,即穿过的缝隙最多。用哈希表记录缝隙即可。
int leastBricks(vector>& wall) {
map map1;
for (int i = 0; i < wall.size(); ++i) {
int tmp = 0;
for (int j = 0; j < wall[i].size() - 1; ++j) {
tmp += wall[i][j];
if(map1.find(tmp) != map1.end()){
// 已存在
map1[tmp] += 1;
} else{
//不存在
map1.insert(make_pair(tmp, 1));
}
}
}
int maxVal = INT_MIN; //穿过最多的缝隙
map::iterator iterator;
for (iterator = map1.begin(); iterator != map1.end() ; iterator++) {
if(iterator->second > maxVal){
maxVal = iterator->second;
}
}
if(maxVal < 0){ // maxVal没有改变的情况
maxVal = 0;
}
return wall.size() - maxVal; //穿过最少的砖
} 3.困难题目
3.1N皇后问题(回溯算法)
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。
![]()
每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/n-queens
这是初学回溯经典的一个例子,落子要考虑和之前的皇后不能有冲突(不能再一条直线上,不能在一条斜线上)。
从空棋盘开始,把皇后1放在第一行第一列。然后放皇后2,1、2列尝试失败,把它放在第三个位置,即格子(2,3),但是这被证明是一个死胡同,因为皇后三将无位置可以放,因此皇后2回溯到(2,4),这样皇后3可以放到(3,2),但是这又是另一个死胡同。就这样不断的向下试探,不行就回溯到上层,直到找到最终的完整解。以下给出4皇后的状态空间树:
bool judge(int dep, int i, vector temp){
//判断如果该位置放置皇后,会不会产生冲突
for(int j = 0; j < temp.size(); j++){
for(int k = 0; k < temp[j].length(); k++){
if(temp[j][k] == 'Q' && (k == i || abs(dep - j) == abs(i - k)))
return false;
}
}
return true;
}
void traceback(int n, int dep, vector> &res, vector &temp){
if(dep == n){
res.push_back(temp);
return;
}
for(int i = 0; i < n; i++){
if(judge(dep, i, temp)){
string str;
for(int j = 0; j < n; j++){
if(j == i)
str.push_back('Q');
else
str.push_back('.');
}
temp.push_back(str); //先将该行加入temp,返回时会弹出
traceback(n, dep + 1, res, temp);
temp.pop_back();
}
}
}
vector> solveNQueens(int n) {
vector> res;
vector temp;
traceback(n, 0, res, temp);
return res;
}
int main() {
vector> res = solveNQueens(1);
for(int i = 0; i < res.size(); i++){
for(int j = 0; j < res[i].size(); j++){
cout << res[i][j] << endl;
}
}
return 0;
}