Asymmetric numeral systems 翻译

本文是对Asymmetric numeral systems: entropy coding combining speed of Huffman coding with compression rate of arithmetic coding的翻译。

Abstract

现代数据压缩主要基于两种熵编码方法：霍夫曼（HC）和算术/范围编码（AC）。前者速度更快，但是以2的幂次近似于概率，通常导致较低的压缩率。后者使用几乎精确的概率，容易接近理论压缩率极限（Shannon熵），但以更大的计算成本为代价。

非对称数字系统（ANS）是一种用于精确熵编码的新方法，它可以结束速度和速率之间的折衷：对于256个大小的字母，最新的实现方法的解码速度比HC快50％，压缩率类似于AC。此优势是因为它比AC更简单：使用单个自然数作为状态，而不是使用两个自然数来表示范围。除了简化重新规范化之外，它还允许将给定概率分布的整个行为放入一个相对较小的表中：定义熵编码自动机。对于256个大小的字母，此表的存储成本为几千字节。选择特定表时有很大的自由度-使用为此目的使用加密密钥初始化的伪随机数生成器可以同时加密数据。

本文还介绍和讨论了这种新的熵编码方法的许多其他变体，它们可以为标准AC，大字母范围编码（large alphabet range coding）或近似准算术编码（approximated quasi arithmetic coding）提供直接替代。

1.Introduction

在标准数字系统中，不同的数字被视为包含相同数量的信息：二进制系统中为1位，或者基本b数字系统中通常为$lg(b)$位（$lg\equiv lo{g}_2$）。但是，概率为$p$的事件包含$lg(1/p)$位信息。因此，尽管标准数字系统对于统一的数字概率分布是最佳的，但是为了最佳地编码通用分布（这是数据压缩的核心），我们应该尝试以某种方式使该概念不对称。我们可以通过这种方式获得算术/范围编码（AC）（[10]，[9]）或最新的不对称数字系统（ANS）（[2]，[3]），具体取决于我们添加后续数字的位置。

具体来说，在标准的二进制数字系统中，将信息存储在自然数$x$（具有m位）中，我们可以通过两种基本方式添加来自数字$s\in (0,1)$的信息：在最高有效位置$（x\to x+2^{m}s）$或最低有效位置$（x\to 2x+s）$。前者意味着新数字在较大范围之间进行选择-我们可以通过更改这些范围的比例，进行算术/范围编码来使其不对称。但是，在标准数字系统中，我们需要记住该最高有效数字（m）的位置，而AC需要指定给定时刻的范围-其当前状态是代表范围的两个数字。

相反，在最不重要的位置添加信息时，当前状态只是一个自然数。对于非对称化来说，这个优势仍然存在：ANS。尽管在标准二进制系统中，x成为对应的偶数（s = 0）或奇数（s = 1）的第x个出现，但是这次我们想将N的这种分裂重新定义为偶数和奇数。这样它们仍然“均匀分布”，但是具有不同的密度-对应于我们想要编码的符号概率分布，如图1所示。

让我们从信息论的角度来看这两种方法。对于AC，知道我们当前在给定范围的一半中就值得1位信息，因此当前内容是lg（范围大小/子范围大小）位的信息。在对概率p的符号进行编码时，子范围的大小乘以p，从而按预期将信息内容增加$lg(1/p)$位。从ANS的角度来看，看到x包含信息的$lg(x)$位，则信息内容应增加到$lg(x)+lg(1/p)=lg(x/p)$位，同时添加概率$p$的符号。因此，我们需要确保$x\to \approx x/p$过渡关系。直观地，规则：如果该子集以$Pr(s)$密度均匀分布，则x成为第s个子集的第x个出现，满足此关系。

霍夫曼编码可以看作是一种无记忆编码器：类型为“符号→位序列”的规则集。 它将每个符号转换为自然数位，以1/2的幂来近似其概率。 从理论上讲，它可以通过对多个符号进行分组来尽可能接近容量（香农熵）。 但是，我们可以在图2中看到，这种收敛速度相对较慢：在此处获得∆H≈0.001位/符号将是完全不切实际的。 可以在[11]中找到精确的分析。

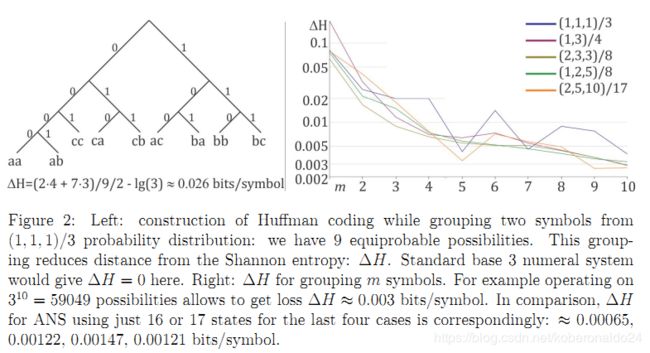
让我们总体上看一下近似概率的代价。 如果我们使用的编码器可以完美地编码$(q_s)$个符号分布来编码$(p_s)$个符号序列，则每个符号平均使用${\sum }_s{p}_{s}lg(1/q_s)$位，而只需要香农熵：${\sum }_s{p}_{s}lg(1/q_s)$。 它们之间的差异称为Kullback-Leiber距离：

其中称为不准确度。

因此，要比霍夫曼收敛更好，我们需要更准确的编码器-我们需要处理小数位数。可以通过向编码器添加一个包含非整数位数的memory/buffer来完成。编码器成为有限状态自动机，具有

type (symbol, state) → (bit sequence, new state)
类型（符号，状态）→（位序列，新状态）编码规则。

如前所述，当前状态在AC情况下包含$lg（范围大小/子范围大小）$位，在ANS情况下包含$lg(x)$位。允许这种状态包含大量位将要求在AC中以较高的精度进行操作，或者在ANS中以较大的arithmetric进行操作-这是不切实际的。为了防止这种情况，在AC中，我们会定期执行重新规范化：如果子范围在范围的一半内，我们可以将单个bit发送到流（指向该一半），然后将这一半重新缩放到整个范围。类似地，我们需要在ANS中收集累积的位：将状态的某些最低有效位传输到流中，以便在对给定符号进行编码后返回固定范围$（I=1，..，2l-1）$。与AC相比，此处的位数很容易确定。$I=4,5,6,7$ 的这种基于4状态ANS的自动机的示例可以在图3中看到：虽然1/4概率的符号b总是产生2位信息，但是符号“ a”为3 / 4概率通常通过增加状态来累积信息，最终产生完整的信息。解码时，每个状态都知道要使用的位数。

本文介绍并讨论了应用ANS方法或其二进制案例的许多变体：非对称二进制系统（ABS）。它们中的大多数在算术编码系列中几乎都有直接的替代方案：

现在将简要描述这些变体。 ANS方法的最初优点是更简单的重新规范化(renormalization)。 在AC中，通常需要使用slow branches来提取单个bit，此外，当范围包含中间点时，还会出现问题。 这些计算上昂贵的问题在ANS中消失了：我们可以从x迅速推断出要在给定步骤中使用的位数，或者将它们存储在表中-我们只需要每步一次直接传输整个位块，从而使其速度更快。

uABS代表用于均匀分布符号( uniformly distributing symbols)的直接​​算术公式。 rABS代表在范围内分配符号(distributing symbols in ranges)-导致仍然是直接公式，准确度稍差但计算更简单。它的主要优点是允许使用较大的字母版本：rANS，可以看作范围编码的直接替代方法，但有一个小的优点：而不是每步2个乘法，它只需要一个即可。我们也可以把uABS的行为变成表格(tables)，得到tABS。它可以像许多AC近似之一一样类似地应用，例如，现代视频压缩中的CABAC [8]中使用的M编码器。 [7]中提供了tABS（fpaqb）和uABS（fpaqc）的Matt Mahoney实现。
虽然那些非常精确的版本可以很容易地在$∆H\approx 0.001bits/symbol$以下的数量级上工作，但qABS类似于准算术编码[5]近似值：我们希望构建一个小的熵编码自动机家族，这样我们就可以涵盖（二进制）概率分布的整个空间。对于qABS，对于$\Delta H\approx 0.01bits/symbol$丢失，它是5个具有5个状态的自动机，对于$\Delta H\approx 0.001bits/symbol$，它是具有16个状态的大约20个自动机。
尽管上述可能性可能不会带来真正的本质优势，但由于状态空间要小得多，tabled ANS将大alphbet 的整个行为放入了一个相对较小的编码表中，这对于AC方法而言可能太过苛刻了。此tANS有可用的交互式演示：[4]。对于ΔH≈0.01位/符号丢失，这种自动机的状态数应比字母大小大大约2-4倍，而对于ΔH≈0.001位/符号则大约为8-16倍。对于256个大小的字母，这意味着每个此类编码表的存储成本为1-16kB。通常，ΔH随状态数的平方下降：将状态数加倍意味着ΔH约小4倍。就像标题中那样，我们获得了非常快的熵编码：最近的Yann Collet实现[1]比Huffman编码的快速实现具有50％的解码速度，并且压缩率几乎最佳-结合了Huffman和算术编码的优点。
选择给定参数的编码表时有很大的自由度：每个符号分布都定义了本质上不同的编码。我们还将讨论此熵编码器混乱行为的三个原因：不对称，遍历和扩散，这使得在没有完整知识的情况下跟踪状态的任何尝试都极为困难。这两个原因建议也将其用于加密应用程序：使用通过加密密钥初始化的伪随机数生成器来选择确切的simbol分配/编码。这样，我们就同时获得了对编码数据的良好加密。

2. Basic concepts and versions

现在，我们将介绍用于以自然数编码信息的基本概念，并找到uABS，rABS和rANS情况的解析公式。

2.1 Basic concepts

给定一个字母表$A=0，..，n-1$，并假设概率分布${ps}_{s\in A}$，${\sum }_s{p}_s=1$。此部分的状态$x\in N$将包含整个已处理的符号序列。
我们需要找到编码（C）和解码（D）函数。 前者取$x\in N$和符号$s\in A$ 的状态，并将它们转换成$x^{\prime }\in N$并存储它们中的信息。 将x视为从$0,1，..，x-1$间隔中选择数字的可能性，它包含$lg（x）$bit 信息。 概率$p_s$的符号s包含信息的$lg（1/p_s）$位，因此$x_0$应包含大约$lg（x）+lg（1/p_s）=lg（x/p_s）$信息位：$x_0$应当近似于$x/p_s$，允许从较大的间隔$0,1，..，x_0-1$中选择一个值。 最后，我们将具有定义单个步骤的函数：
对于标准二进制系统，我们有$C(s，x)=2x+s$，$D（x_0）=（mod（x，2）,x/2)$，我们可以看到s在偶数和奇数之间进行选择。 如果我们假设x在某个间隔中选择偶数（或奇数），则$x_0=2x+s$在该间隔中的所有数字之间进行选择。
对于一般情况，我们将不得不重新定义对应于不同s的子集：像偶数/奇数一样，它们仍应均匀覆盖$N$，但是这次具有不同的密度：$\{ps{\}}_{s\in A}$。 我们可以通过符号分布s来定义$N$的这种划分：$N\to A$

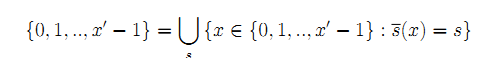
在标准二进制系统中，$x_0$是偶数/奇数的第x个出现，但是这次它将是第s个子集的第x个出现。 因此解码功能将是

$C(s，x_s)=x$是它的反转。显然，我们有$x={\sum }_s{x}_s$。
由于$x/x_s$是我们目前用于编码符号$s$的位数，为了减少不准确度，因此ΔH，我们希望$x_s\approx x{p}_s$近似值尽可能接近-直观上意味着符号几乎与$\{p_s\}$密度独立分布。现在，我们仅通过取$x1:=[x_p]$就可以找到二进制情况的公式，在第4节中，我们将集中讨论在较大字母的固定间隔上找到这种近似均匀的分布。
最后，我们可以想象x是符号的堆栈，C是push操作，D是pop操作。当前的编码算法将是： x = 1，然后将C与后续符号一起使用。这将导致自然数很大，我们可以使用D以相反的顺序从中提取所有符号。为防止对大数进行不方便的运算，在下一节中，我们将讨论流版本，在该版本中，将累积的完整位提取为使x保持在固定间隔I中。

2.2 Uniform asymmetric binary systems (uABS)

现在，我们将为二进制情况和几乎均匀的符号分布找到一些明确的公式：$A=\{0,1\}$。

此公式的起始值和$p=0.3$表示在图1的右下角。这是通过插入后续符号进行编码的示例：

2.3 Range variants (rABS, rANS)

现在，我们将介绍另一种方法，其中将符号外观放置在范围内。 它的准确性较差，但执行的成本可能较低。 最重要的是，它允许使用较大的字母，从而可以直接替代范围编码-这次每个符号使用单个乘法，而不是范围编码中需要两个乘法。 可以将这种方法视为采用标准数字系统并合并其一些后续数字。
我们将从二进制示例（rABS）开始，然后定义通用公式。
示例：查看$（1,3）/4$概率分布，我们想采用标准的以4为底的数字系统：使用数字0、1、2、3并仅合并其3个数字-假设1、2和3 因此，尽管标准三元系统的符号分布为$s(x)=mod(x,4)$：循环（0123），但我们将其不对称化为（0111）循环分布：

类似地，我们可以为不同的分数定义编码/解码功能，这是现在将发现的大字母公式的特例：rANS。 假设概率分布是以下形式的一部分：$（l_0，l_1，...，l_{n-1}）/m$,其中$l_s\in N，m={\sum }_s{l}_s$。
现在让我们类似地想象一下，我们从基数m的数字系统开始，然后将对应的后续数字的数字合并在一起：符号分布是循环的$（00..011..1...“n-1”）$，且符号s的外观为$l_s$ 。 让我们在此循环中将$s(x)$定义为$x\in [0，..，m-1]$位置中的符号：

如果我们选择m作为2的幂，则可以通过移位，乘以除以mod（x，m）并使用掩码进行乘以除法-解码每步仅需一次乘法。
相反，在范围编码中，需要两个-这种方法应该更快。

3 Stream version - encoding finite-state automaton

3.1 Algorithm

3.2 Example

3.3 Necessary condition and remarks for stream formulas

3.4 Analysis of a single step

3.5 Stationary probability distribution of states

3.6 Bound for ∆H

3.7 Initial state and direction of encoding/decoding

4 Tabled asymmetric numeral systems (tANS)

4.1 Precise initialization algorithm

4.2 Inaccuracy bound

4.3 Quasi ABS (qABS) and tuning

4.4 Combining tANS with encryption

5 Conclusions