[机器学习]决策树中的信息增益和信息增益比
一、特征选择中的信息增益
什么是信息增益?
信息增益是特征选择中的一个重要的指标,它定义为一个特征能为分类系统带来多少信息,信息越多,该特征就越重要。
这样就又有一个问题:如何衡量一个特征为分类系统带来了多少信息呢?
对一个特征而言,系统有它的时候和没有它的时候信息量将会发生变化,前后的信息量的差值就是这个特征给系统带来的信息量。
信息量——在信息论中就是熵。
二、计算信息增益:利用熵
1.信息论中的熵
有一个随机变量x,它可能的取值有n种,x1,x2,......,xn,每一种取到的概率是p1,p2,......,pn,那么x的熵就定义为:
式中的对数以2为底的时候熵的单位是比特(bit),以e为底的时候单位是纳特(nat)。
意思就是一个变量可能的变化越多(就是取值的种类越多,反而跟变量具体的取值没有任何关系,只和值的种类多少以及发生概率有关),它携带的信息量就越大。
2.分类系统中的熵
对分类系统来说,类别C是变量,它可能的取值是C1,C2,……,Cn,而每一个类别出现的概率是P(C1),P(C2),……,P(Cn),因此n就是类别的总数。此时分类系统的熵就可以表示为:
3.信息增益和熵的关系
信息增益是针对一个一个的特征而言的。那么我们就是一个一个特征来看,系统含有特征a时的信息量很好计算,就是上面的式子,它表示的是包含所有特征时的信息量。
当系统中不包含特征a时,信息量(熵)该如何计算?
这里有一个例子:教室里有很多座位,学生们每次上课进来的时 候可以随便坐,因而变化是很大的(无数种可能的座次情况);但是现在有一个座位,看黑板很清楚,听老师讲也很清楚,于是校长的小舅子的姐姐的女儿托关系 (真辗转啊),把这个座位定下来了,每次只能给她坐,别人不行,此时情况怎样?对于座次的可能情况来说,我们很容易看出以下两种情况是等价的:(1)教室 里没有这个座位;(2)教室里虽然有这个座位,但其他人不能坐(因为反正它也不能参与到变化中来,它是不变的)。
从例子中可以看出,下面两个命题是等价的:1.系统中不包含特征a。2.系统中包含特征a,但是a已经固定,不能变化。
那么我们计算系统中不包含特征a的情况时,就用2来代替。当一个特征a不能变化时,系统的信息量是多少?
这个信息量有个专门的名称:条件熵。
一个特征X,它可能的取值有n多种(x1,x2,……,xn), 当计算条件熵而需要把它固定的时候,要把它固定在哪一个值上呢?答案是每一种可能都要固定一下,计算n个值,然后取均值才是条件熵。而取均值也不是简单的 加一加然后除以n,而是要用每个值出现的概率来算平均(简单理解,就是一个值出现的可能性比较大,固定在它上面时算出来的信息量占的比重就要多一些)。
条件熵的表达式:
特征x被固定为xi时的条件熵。
特征x被固定时的条件熵。
上面两个式子的关系。
具体到我们文本分类系统中的特征T,T有几个可能的值呢?注意t是指一个固定的特征,比如他就是指关键词“经济”或者“体育”,当我们说特征“经济”可能的取值时,实际上只有两个,“经济”要么出现,要么不出现。一般的,T的取值只有T(代表t出现)和非T(代表t不出现),注意系统包含t但t 不出现与系统根本不包含t可是两回事。
固定t时条件熵就有了,则
P(t)就是T出现的概率,就是T不出现的概率。式子进一步展开;
那么特征T给系统带来的信息增益为;
三:信息增益比
以信息增益作为划分训练数据集的特征,存在偏向于选择取值较多的特征的问题。使用信息增益比可以对这一问题进行矫正。
特征A对训练数据集D的信息增益比定义为其信息增益与训练数据集D关于特征A的值的熵之比。
式子;
四:一个例子
任务:
根据天气预测否去打网球
数据:
这个数据集来自Mitchell的机器学习,叫做是否去打网球play-tennis,以下数据仍然是从带逗号分割的文本文件,复制到纪事本,把后缀直接改为.csv就可以拿Excel打开: *play-tennis data,其中6个变量依次为:编号、天气{Sunny、Overcast、Rain}、温度{热、冷、适中}、湿度{高、正常}、风力{强、弱}以及最后是否去玩的决策{是、否}。一个建议是把这些数据导入Excel后,另复制一份去掉变量的数据到另外一个工作簿,即只保留14个观测值。这样可以方便地使用Excel的排序功能,随时查看每个变量的取值到底有多少。*/ NO. , Outlook , Temperature , Humidity , Wind , Play 1 , Sunny , Hot , High , Weak , No 2 , Sunny , Hot , High , Strong , No 3 , Overcast , Hot , High , Weak , Yes 4 , Rain , Mild , High , Weak , Yes 5 , Rain , Cool , Normal , Weak , Yes 6 , Rain , Cool , Normal , Strong , No 7 , Overcast , Cool , Normal , Strong , Yes 8 , Sunny , Mild , High , Weak , No 9 , Sunny , Cool , Normal , Weak , Yes 10 , Rain , Mild , Normal , Weak , Yes 11 , Sunny , Mild , Normal , Strong , Yes 12 , Overcast , Mild , High , Strong , Yes 13 , Overcast , Hot , Normal , Weak , Yes 14 , Rain , Mild , High , Strong , No
用决策树来预测:
决策树的形式类似于“如果天气怎么样,去玩;否则,怎么着怎么着”的树形分叉。那么问题是用哪个属性(即变量,如天气、温度、湿度和风力)最适合充当这颗树的根节点,在它上面没有其他节点,其他的属性都是它的后续节点。
那么借用上面所述的能够衡量一个属性区分以上数据样本的能力的“信息增益”(Information Gain)理论。
如果一个属性的信息增益量越大,这个属性作为一棵树的根节点就能使这棵树更简洁,比如说一棵树可以这么读成,如果风力弱,就去玩;风力强,再按天气、温度等分情况讨论,此时用风力作为这棵树的根节点就很有价值。如果说,风力弱,再又天气晴朗,就去玩;如果风力强,再又怎么怎么分情况讨论,这棵树相比就不够简洁了。
用熵来计算信息增益:
1 计算分类系统熵 类别是 是否出去玩。取值为yes的记录有9个,取值为no的有5个,即说这个样本里有9个正例,5 个负例,记为S(9+,5-),S是样本的意思(Sample)。那么P(c1) = 9/14, P(c2) = 5/14
这里熵记为Entropy(S),计算公式为:
Entropy(S)= -(9/14)*log2(9/14)-(5/14)*log2(5/14)用Matlab做数学运算
2 分别以Wind、Humidity、Outlook和Temperature作为根节点,计算其信息增益 我们来计算Wind的信息增益
当Wind固定为Weak时:记录有8条,其中正例6个,负例2个;
同样,取值为Strong的记录6个,正例负例个3个。我们可以计算相应的熵为:
Entropy(Weak)=-(6/8)*log(6/8)-(2/8)*log(2/8)=0.811 Entropy(Strong)=-(3/6)*log(3/6)-(3/6)*log(3/6)=1.0
现在就可以计算出相应的信息增益了:
所以,对于一个Wind属性固定的分类系统的信息量为 (8/14)*Entropy(Weak)+(6/14)*Entropy(Strong)
Gain(Wind)=Entropy(S)-(8/14)*Entropy(Weak)-(6/14)*Entropy(Strong)=0.940-(8/14)*0.811-(6/14)*1.0=0.048
这个公式的奥秘在于,8/14是属性Wind取值为Weak的个数占总记录的比例,同样6/14是其取值为Strong的记录个数与总记录数之比。
同理,如果以Humidity作为根节点: Entropy(High)=0.985 ; Entropy(Normal)=0.592 Gain(Humidity)=0.940-(7/14)*Entropy(High)-(7/14)*Entropy(Normal)=0.151 以Outlook作为根节点: Entropy(Sunny)=0.971 ; Entropy(Overcast)=0.0 ; Entropy(Rain)=0.971 Gain(Outlook)=0.940-(5/14)*Entropy(Sunny)-(4/14)*Entropy(Overcast)-(5/14)*Entropy(Rain)=0.247 以Temperature作为根节点: Entropy(Cool)=0.811 ; Entropy(Hot)=1.0 ; Entropy(Mild)=0.918 Gain(Temperature)=0.940-(4/14)*Entropy(Cool)-(4/14)*Entropy(Hot)-(6/14)*Entropy(Mild)=0.029 这样我们就得到了以上四个属性相应的信息增益值: Gain(Wind)=0.048 ;Gain(Humidity)=0.151 ; Gain(Outlook)=0.247 ;Gain(Temperature)=0.029 最后按照信息增益最大的原则选Outlook为根节点。子节点重复上面的步骤。这颗树可以是这样的,它读起来就跟你认为的那样:
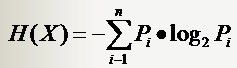
![[机器学习]决策树中的信息增益和信息增益比_第1张图片](http://img.e-com-net.com/image/info8/3fd97296df604608b61e2122c77136cf.jpg)


![[机器学习]决策树中的信息增益和信息增益比_第2张图片](http://img.e-com-net.com/image/info8/006fa5e105974d928a0668083f6caa59.jpg)