机器学习笔记（10）——逻辑回归算法优化之随机梯度下降法

在上一篇文章《机器学习笔记（9）——深入理解逻辑回归算法及其Python实现》中，详细学习了逻辑回归算法的分类原理和使用梯度下降法来最小化损失函数的数学推导过程，从而拟合出分类函数的参数θ。

1. 随机梯度下降

还记得参数θ的迭代公式吗：

可以看出，每次迭代更新参数θ都需要遍历整个数据集，计算复杂度取决于样本的个数和样本的特征值数，真实情况下，往往样本数不只100个，特征值也不只2个，那么计算的复杂度会相当高。因此考虑用随机梯度下降算法——一次只用一个样本来更新参数。

随机梯度下降算法的Python代码如下：

# -*- coding: cp936 -*-
import matplotlib.pyplot as plt
from numpy import *

plt.rcParams['axes.unicode_minus'] = False


# 加载数据集，返回样本属性值矩阵和类别向量
def loadDataSet():
    dataMat = []
    labelMat = []
    fr = open(r'D:\Projects\PyProject\Logistic\testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat, labelMat


# sigmoid函数
def sigmoid(inX):
    return 1.0 / (1 + exp(-inX))


# 随机梯度上升算法
def stocGradAscent0(dataMatrix, classLabels):
    m, n = shape(dataMatrix)
    alpha = 0.01
    weights = ones(n)
    for i in range(m):
        h = sigmoid(sum(dataMatrix[i] * weights))
        error = (h - classLabels[i])
        weights = weights - alpha * dataMatrix[i] * error
    return weights


# 画数据集和逻辑回归最佳拟合直线
def plotBestFit(thetas):
    dataMat, labelMat = loadDataSet()
    dataArr = array(dataMat)
    n = shape(dataArr)[0]
    xcord1 = []
    ycord1 = []
    xcord2 = []
    ycord2 = []
    for i in range(n):
        if int(labelMat[i]) == 1:
            xcord1.append(dataArr[i, 1])
            ycord1.append(dataArr[i, 2])
        else:
            xcord2.append(dataArr[i, 1])
            ycord2.append(dataArr[i, 2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
    ax.scatter(xcord2, ycord2, s=30, c='green')
    x = arange(-3.0, 3.0, 0.1)
    y = (-thetas[0] - thetas[1] * x) / thetas[2]
    # y = y.getA1()
    ax.plot(x, y)
    plt.xlabel('X1')
    plt.ylabel('X2')
    plt.show()


if __name__ == '__main__':
    dataMat, labelMat = loadDataSet()
    thetas = stocGradAscent0(array(dataMat), labelMat)
    plotBestFit(thetas)

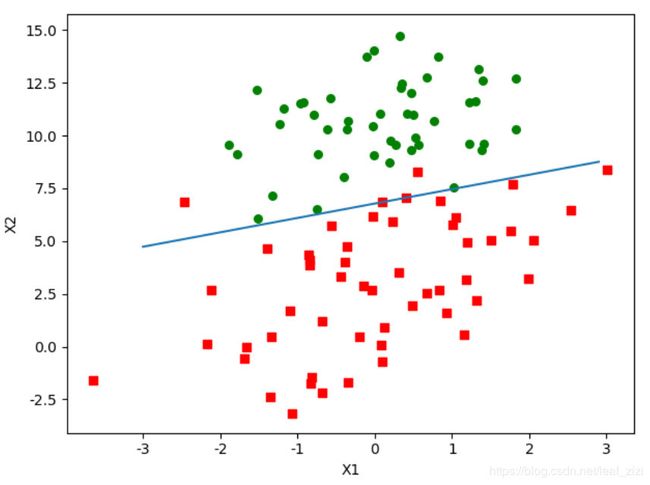
看一下分类的效果：

可以看出，决策边界左上方的红点被错误分类，因为我们只做了100次迭代，而且每次迭代只用了一个数据样本。

判断一个算法优劣的方法是看其是否收敛，即参数是否达到稳定值。我们对上面的算法做一些改进，让其运行200次，并且绘制参数的变化趋势，对stocGradAscent0方法做如下修改，同时添加绘制参数的方法plotThetas：

# 随机梯度上升算法
def stocGradAscent0(dataMatrix, classLabels, numIter=200):
    m, n = shape(dataMatrix)
    alpha = 0.01
    weights = ones(n)
    theta0 = []
    theta1 = []
    theta2 = []
    for j in range(numIter):
        for i in range(m):
            h = sigmoid(sum(dataMatrix[i] * weights))
            error = (h - classLabels[i])
            weights = weights - alpha * dataMatrix[i] * error
            theta0.append(weights[0])
            theta1.append(weights[1])
            theta2.append(weights[2])
    print(theta0)
    print(theta1)
    print(theta2)
    plotThetas(theta0,theta1,theta2)
    return weights


def plotThetas(theta0, theta1, theta2):
    fig = plt.figure()
    ax0 = fig.add_subplot(311)
    ax0.plot(theta0)
    plt.ylabel('theta0')
    ax1 = fig.add_subplot(312)
    ax1.plot(theta1)
    plt.ylabel('theta1')
    ax2 = fig.add_subplot(313)
    ax2.plot(theta2)
    plt.ylabel('theta2')
    plt.show()

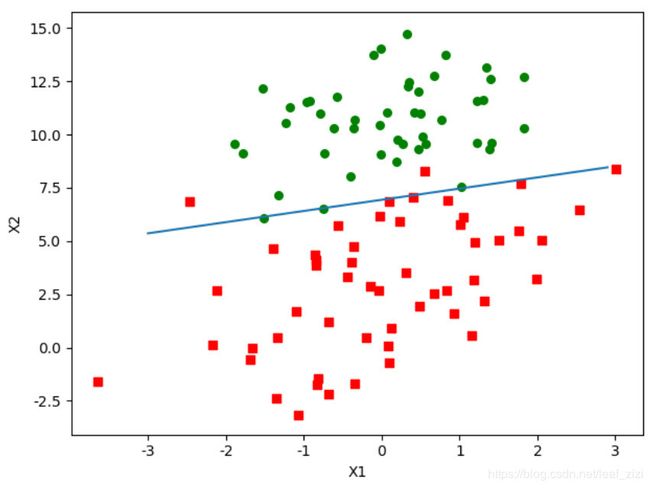
运行效果如下，可以看出随机梯度法循环200次的分类效果与非随机梯度法的分类效果几乎相同，而前者比后者少进行了300*100次的运算。再看参数变化趋势，θ1和θ2在循环100次后变化趋于平稳，θ0的值仍然在缓慢上升，而且每个参数仍有小的周期性波动，这是因为有一些样本点无法线性正确分类造成的。

我们尝试把循环的次数改为100，得到的分类效果如下，比循环200次只多了两个分类错误的样本，而运算量却降低了一半。

2. 改进随机梯度下降法

为了提高收敛速度，以及解决因错误样本产生的周期性波动问题，还可以对代码做两处优化：1是每次迭代时调整alpha的值，以缓解波动；2是每次随机选取一个样本，然后从列表中删除该值（保证样本在一次循环中不重复）。

# 改进的随机梯度上升算法
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
    m, n = shape(dataMatrix)
    weights = ones(n)
    theta0 = []
    theta1 = []
    theta2 = []
    for j in range(numIter):
        dataIndex = list(range(m))
        for i in range(m):
            alpha = 4 / (1.0 + j + i) + 0.01  # 每次迭代都调整alpha值，用来缓解数据波动
            randIndex = int(random.uniform(0, len(dataIndex)))  # 每次随机取一个样本
            h = sigmoid(sum(dataMatrix[randIndex] * weights))
            error = (h - classLabels[randIndex])
            weights = weights - alpha * dataMatrix[randIndex] * error
            del (dataIndex[randIndex])  # 删除用过的索引，使样本不被重复使用，减少周期性波动
            theta0.append(weights[0])
            theta1.append(weights[1])
            theta2.append(weights[2])
    plotThetas(theta0, theta1, theta2)
    return weights


if __name__ == '__main__':
    dataMat, labelMat = loadDataSet()
    thetas = stocGradAscent1(array(dataMat), labelMat,40)
    print(thetas)
    plotBestFit(thetas)

循环的次数默认设为150，而调用方法时我们设置40次循环，看一下运行效果，很明显，参数的收敛速度更快，而且没有出现明显的周期性波动，分类的效果也不错，而运算量只有40*100次。

3. 总结

本文中，我们学习了随机梯度下降法，即每次仅用一个样本训练参数，并且通过观察参数的变化趋势，找到合适的迭代次数。进一步通过改进随机梯度下降法中的alpha值和样本选取规则，加快了收敛的速度、避免了参数的周期性波动，最后仅用了40次迭代就近乎达到了500次迭代的分类效果。

 

---

逻辑回归算法原理和数学推导过程请参考：​​

机器学习笔记（9）——深入理解逻辑回归算法及其Python实现

资源下载：https://download.csdn.net/download/leaf_zizi/11015182

---

参考：

Peter Harrington 《机器学习实战》