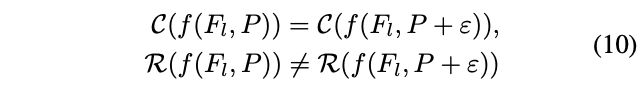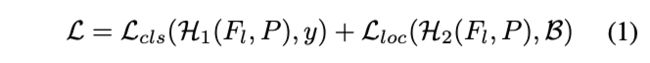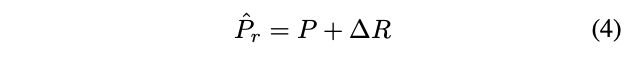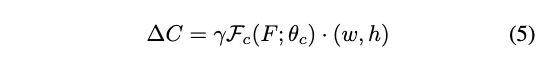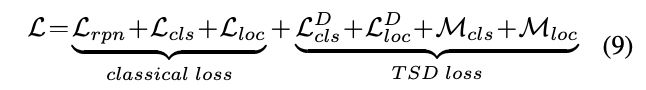商汤提出解偶检测中分类和定位分支的新方法TSD，COCO 51.2mAP | CVPR 2020

目前很多研究表明目标检测中的分类分支和定位分支存在较大的偏差，论文从sibling head改造入手，跳出常规的优化方向，提出TSD方法解决混合任务带来的内在冲突，从主干的proposal中学习不同的task-aware proposal，同时结合PC来保证TSD的性能，在COCO上达到了51.2mAP
 
来源：晓飞的算法工程笔记 公众号

论文: Revisiting the Sibling Head in Object Detector

• 论文地址：https://arxiv.org/abs/2003.07540

Introduction

---

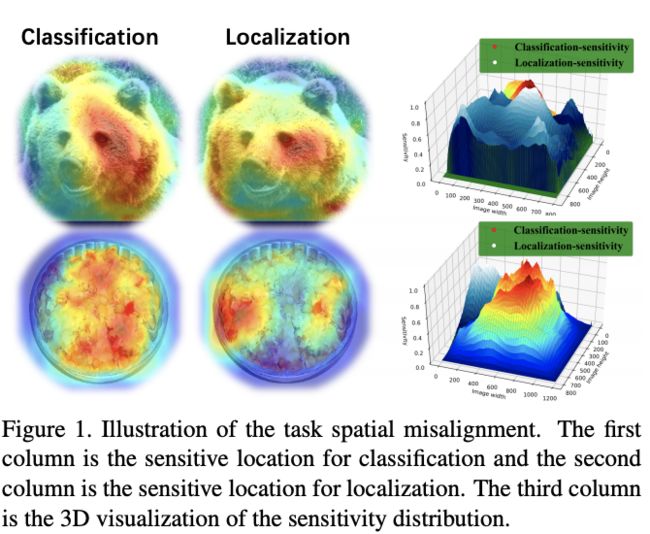
  经典RoI-based定位算法使用sibling head(2-fc)对proposal同时进行分类和回归，由于任务的本质不同，分类任务和定位任务是完全不同的，关注的特征也不一样，如图1所示。分类任务往往需要平移不变性，而定位任务则需要平移可变性。

  具体属性的表现如公式10所示，${\forall }_{\epsilon },IoU(P+\epsilon ,\mathcal{B})\ge T$，$T$为IoU阈值，$f$为共用的特征提取器。因此，共用的特征提取器以及相同的proposal都是目标检测学习的主要障碍。
  与以往的方法不同，论文观察到限制定位算法的根本问题在于分类分支和定位分支在空间维度上存在偏差，不是通过设计特征提取器或更好的结构能解决的。因此，论文提出TSD方法，从空间维度和特征提取两方面同时对分类任务和定位任务进行拆解，并且结合精心设计的渐进约束(PC)帮助学习。
  论文的贡献如下：

• 深入探讨RoI-based检测算法中混合任务带来的障碍，并揭示限制检测性能的瓶颈
• 提出TSD(task-aware spatial disentanglement)解决混合任务的冲突，能够学习到task-specific特征表达能力
• 提出PC(progressive constraint)来扩大TSD和sibling head间的性能间隔
• 在COCO和OpenImage上验证了有效性，单模型最高可达51.2mAP

Methods

---

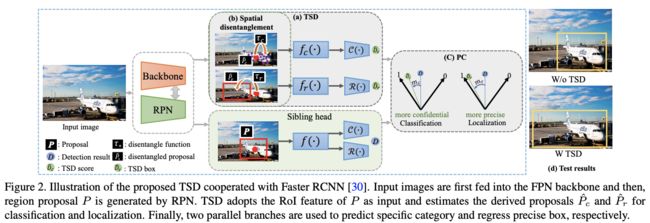
  如图2所示，在训练时，TSD和原来的结构共存，定义主干输出的预测框为$P$，TSD输出最终的定位结果${\hat{D}}_r$和最终的分类结果${\hat{D}}_c$，原sibling head输出的结果为$D$，GT为$\mathcal{B}$，类别为$y$

TSD (task-aware spatial disentanglement)

  经典的Faster RCNN基于$P$同时最小化预测框的分类误差和损失误差，如公式1，${\mathcal{H}}_1(\cdot )=\{f(\cdot ),\mathcal{C}(\cdot )\}$，${\mathcal{H}}_2(\cdot )=\{f(\cdot ),\mathcal{R}(\cdot )\}$，$f(\cdot )$为特征提取，$\mathcal{C}(\cdot )$和$\mathcal{H}(\cdot )$为分别从特征进行分类和定位的预测函数。由于分类和定位所用到的特征不太一样，一些研究将特征提取拆分为$f_c$和$f_r$，尽管这样的拆分能带来一些提升，但任务混合在空间上的内在冲突仍然潜在(分类和定位所需的bbox其实不一样)

  为了解决这个潜在的问题，TSD直接在空间上对分类和定位进行分解，如公式2，从原预测框$P$中预测出分类框${\hat{P}}_c={\tau }_c(P,\Delta C)$以及定位框${\hat{P}}_r={\tau }_r(P,\Delta R)$，$\Delta C$为pointwise的形变，$\Delta R$为proposal-wise的变化，具体如图2(b)所示。然后再通过不同的特征提取和head进行分类和定位的预测，${\mathcal{H}}_1^D(\cdot )=\{f_c(\cdot ),\mathcal{C}(\cdot )\}$，${\mathcal{H}}_2^D(\cdot )=\{f_r(\cdot ),\mathcal{R}(\cdot )\}$。由于分解了分类和定位的预测区域，TSD能够学习task-aware的特征表达。

TSD learning

  对于定位，使用三层全连接${\mathcal{F}}_r$来生成proposal-wise变化$\Delta R\in {\mathbb{R}}^{1\times 1\times 2}$用于将$P$转换为${\hat{P}}_r$，每层的输出为$\{256,256,2\}$，$\gamma$为预设的调节标量。${\tau }_r$的计算如公式4，即将$P$进行整体移动，新点的值使用双线性插值计算，使得$\Delta R$可微。

  对于分类，将规则的$P$变形为不规则的${\hat{P}}_c$，${\mathcal{F}}_c$为三层全连接层，每层的输出为$\{256,256,k\times k\times 2\}$，为了减少参数，首层全连接与${\mathcal{F}}_r$共用。$\Delta C\in {\mathbb{R}}^{k\times k\times 2}$为pointwise的x坐标和y坐标变化，$k\times k$为池化后特征${\hat{F}}_c$的大小，根据公式6使用$\Delta C$生成池化后的特征图${\hat{F}}_c$，这里的池化操作跟Deformable Convolution的一样。$|G(x,y)|$为像素总数，具体大小跟池化前后的特征图大小有关，$(p_x,p_y)$为区域中的坐标，${\mathcal{F}}_B(\cdot )$为双线性插值，使$\Delta C$可导。

Progressive constraint

  在训练阶段，使用公式1对TSD和sibling head进行联合训练，此外还设计了渐进约束(progressive constraint, PC)来辅助TSD的学习，如图2©。

  对于分类分支，PC如公式7，$\mathcal{H}(y|\cdot )$为$y$类的置信度，$m_c$约预设的间隔，$|\cdot {|}_{+}$类似于ReLU函数，即约束TSD的预测置信度需要比sibling head至少高$m_r$，否则即学习不够，产生损失

  对于定位分支，PC如公式8，$\hat{\mathcal{B}}$为原方式的最终预测结果，${\hat{\mathcal{B}}}_D$为TSD转换后的最终预测结果，仅对正样本进行计算，即约束TSD的预测结果的IoU需要比sibling head至少高$m_r$

  最终的损失函数为公式9，结合了所有的损失，推理的时候把sibling head分支和PC去掉。
  论文在此处提出的约束方法很好，但是会存在一个问题，若sibling head学习充分了，留给TSD的提升空间本身就小于间隔，这样产生的损失显然有些不合理，所以是否在这种情况应该调整间隔，在可提升空间和预设间隔之间去个最小值。

Experiments

---

Ablation studies

• Task-aware disentanglement

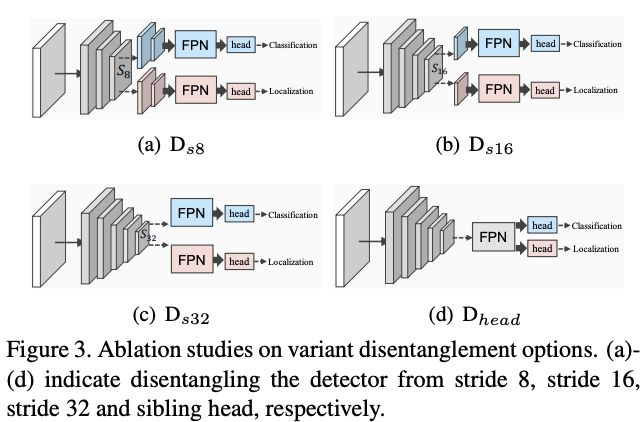
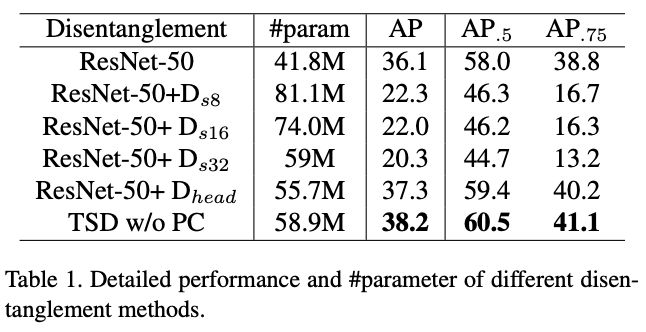
  这里对比了TSD与不同的分解策略，比如$D_{s8}$即从stride为8的特征图开始分解。

• Joint training with sibling head ${\mathcal{H}}_{\ast }$

• Effectiveness of PC

• Derived proposal learning manner for ${\mathcal{H}}_{\ast }^D$

• Delving to the effective PC

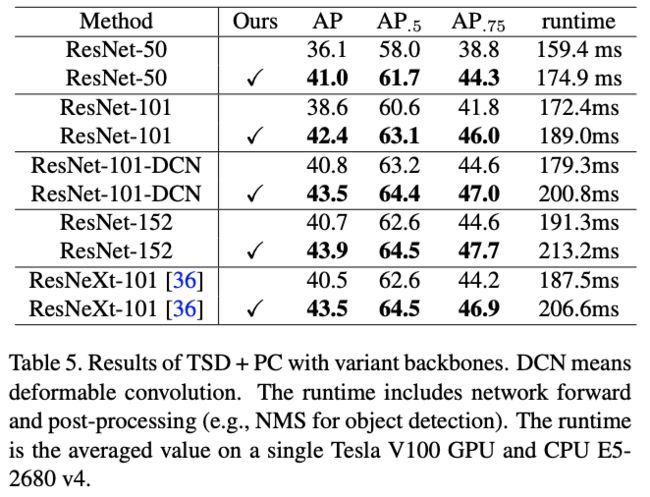
Applicable to variant backbones

  基于Faster R-CNN + TSD替换不同主干网络的结果

Applicable to Mask R-CNN

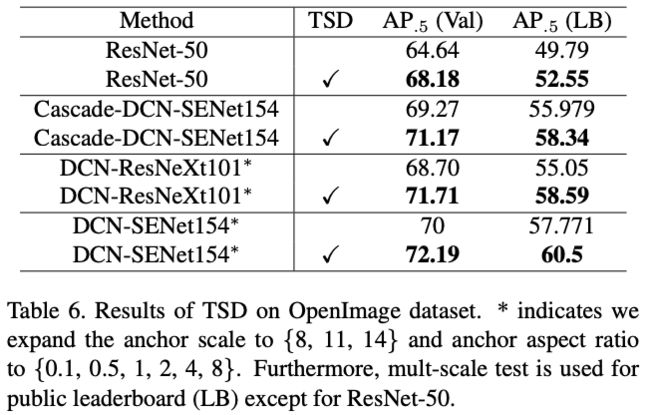
Generalization on large-scale OpenImage

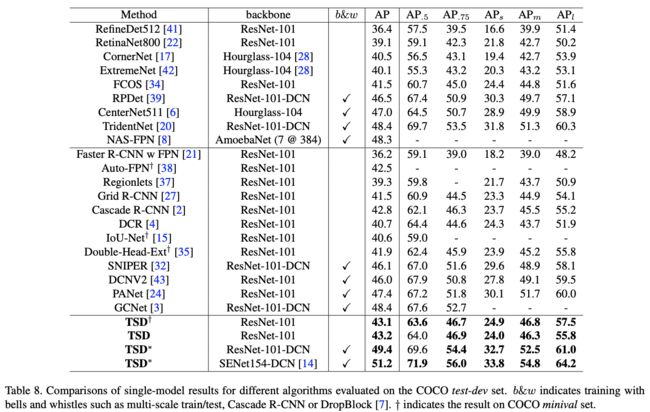
Comparison with state-of-the-Arts

Analysis and discussion

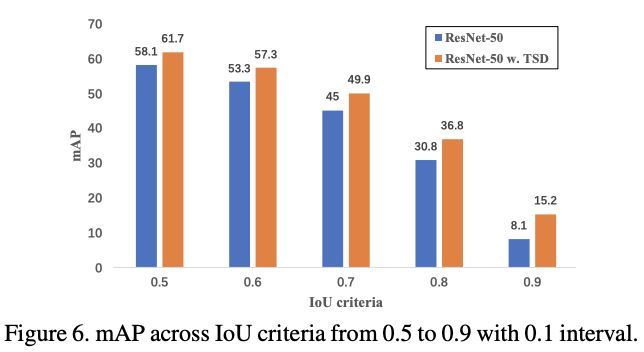
• Performance in different IoU criteria

• Performance in different scale criteria

• What did TSD learn

  从图5可以看出，TSD的定位能够学习不易回归的边界，而分类则专注于局部特征以及目标的上下文信息，这里的点为区域$G(x,y)$转换后的中心点

Conclusion

---

  目前很多研究表明目标检测中的分类分支和定位分支存在较大的偏差，论文从sibling head改造入手，跳出常规的优化方向，提出TSD方法解决混合任务带来的内在冲突，从主干的proposal中学习不同的task-aware proposal，同时结合PC来保证TSD的性能，在COCO上达到了51.2mAP

 
 
 

如果本文对你有帮助，麻烦点个赞或在看呗～
更多内容请关注 微信公众号【晓飞的算法工程笔记】