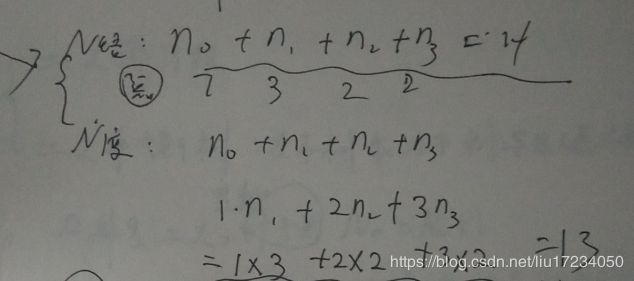数据结构——考前查漏补缺
文章目录:
一:考点部分
第一章:绪论
第二章:线性表
顺序表(SqList)
链式表(LNode LinkList)
第三章:栈和队列【老板-员工】
栈(Stack)-LIFO先进后出【水瓶】
队列(Queue)-FIFO先进先出【排队】
第四章:串【不考】
第五章:数组和广义表【不考】
数组
广义表
第六章:树与二叉树
树
二叉树
线索二叉树
树及其转换
树与二叉树的运用
哈夫曼树
第七章:图
第八章:查找【平均查找长度的算法】
第九章:排序
第一类:插入排序
直接插入排序/简单插入排序:
希尔排序:——【常考】
第二类:交换排序
冒泡排序
快速排序——【常考】
第三类:选择排序
简单选择排序
堆排序【小顶堆 -大顶堆】——【常考】
第四类:归并排序——【常考】
第五类:基数排序(桶排序/数字排序)
第二部分:加强记忆注意部分
第一类:树
1.树的结点数为多少?
2.度为m的树的第i层最多有多少个结点?
3.假设树的高度为k,结点最多、最少有多少个?
4.高度为多少?
5.高度为h的m叉树至多有多少个结点?
6.n个结点的m叉树最小高度为多少?
7. n个结点的m叉树有多少个空指针域?
8.向一棵B_树插入元素的过程中,若最终引起树根结点的分裂,则新树比原树的高度__增加1____。
第二类:二叉树
1.非空二叉树上叶子结点(N0)树为多少?
2.非空二叉树,第k层上至多有多少个结点?
3.高度为h的二叉树至多有多少个结点?
4.设某棵二叉树的高度为h,则该二叉树上叶子结点最多有 2^(h-1)
5.若用链表存储一棵二叉树时,每个结点除数据域外,还有指向左孩子和右孩子的两个指针。在这种存储结构中,n个结点的二叉树共有_____2n___个指针域,其中有__n-1______个指针域是存放了地址,有_____n+1___________个指针是空指针。
第三类:完全二叉树
4.n个结点的完全二叉树的高度为多少?
5.完全二叉树是否有双亲结点-左孩子-右孩子?
6.n个结点的完全二叉树的深度为K,最多、最少有多少个结点?
7.n个结点的完全二叉树的深度为多少?
8.设一棵完全二叉树中有n个结点, 若用二叉链表作为该完全二叉树的存储结构,则共有_____n+1______个空指针域
9.设一棵完全二叉树有128(n)个结点,则该完全二叉树的深度为__8______,有____64_____(n/2)_个叶子结点
第四类:哈夫曼树【正则二叉树】
1.没有度为1的结点
2.哈夫曼树度为2的结点树为多少?
3.哈夫曼树一共有多少个结点?
4.哈夫曼叶子结点(N0)树为多少?
5. 设哈夫曼树中的叶子结点总数为m,若用二叉链表作为存储结构,则该哈夫曼树中总共有2m个空指针域
6.设哈夫曼树中共有n个结点,则该树中有____(n+1)/2____个叶子结点;若采用二叉链表作为存储结构,则该树中有___(n+1)__个空指针域
第五类:循环队列
1.初始时
2.判断队为空
3.判断队为满
4.判断循环队列元素个数
5.设有一个顺序循环队列中有M个存储单元,则该循环队列中最多能够存储___m-1_____个队列元素;当前实际存储___(R-F+M)%M_____________个队列元素(设头指针F指向当前队头元素的前一个位置,尾指针指向当前队尾元素的位置)
第六类:完全图
1.n个顶点的无向完全图有几条边?
2.n个顶点的有向完全图有几条边?
第七类:有向图-无向图
1.有n个顶点,e条边的有向图和无向图在其对应邻接表中所含边的结点分别为多少?
2.设无向图中n个顶点,e条边,顶点和为d
3.设有向图G中有n个顶点e条有向边,所有的顶点入度数之和为d
4.设某有向图中n个顶点,邻接表中有n个表头结点
5.设某有向图的邻接表中有n个表头结点和m个表结点,则该图中有m条有向边
6.设有n个结点的无向图,该图至少应有n-1条边才能确保是一个连通图
7.设无向图G中有n个顶点e条边,则其对应的邻接表中的表头结点和表结点的个数分别为 n,2e
8. 设某无向图中有n个顶点e条边,则该无向图中所有顶点的入度之和为2e
9.设某无向图G中有n个顶点,用邻接矩阵A作为该图的存储结构,则顶点i和顶点j互为邻接点的条件是
10.设无向图对应的邻接矩阵为A,则A中第i行上非0元素的个数___等于______第i列上非0元素的个数(填等于,大于或小于)
11.设无向图G中有n个顶点,则该无向图的最小生成树上有n-1条边
12.设无向图G中有n个顶点,则该无向图中每个顶点的度数最多是n-1个
第八类:连通图——强连通图
1.如果一个图有n个顶点,并且有小于n-1条边——非连通图
2.无向图的顶点数为n,则其含有全部顶点的连通图的边数最小为n-1
3.一个顶点也是强连通子图
4.当n个顶点的图构成一个环,任意两个点之间有回路(环),最小、最大边数为多少?
5.设某强连通图中有n个顶点,则该强连通图中至少有n条边
一:考点部分
第一章:绪论
1.数据元素-数据项的区别用法
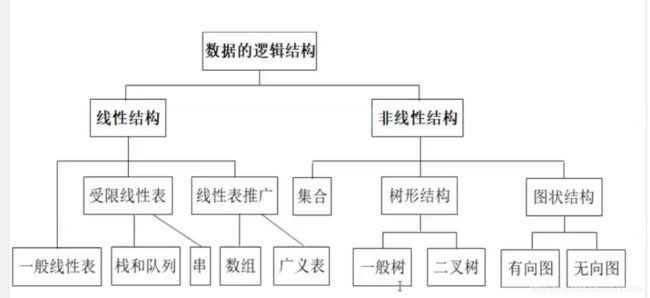
2.逻辑机构【线性结构-集合-树形结构-图形结构】
4.数据的存储结构【顺序存储-链式存储-索引存储-散列存储】
5.抽象数据类型
6.程序和算法
7.算法的特点:有穷性,确定性,可行性,输入性,输出性
8.算法设计的基本要求:正确性,可读性,健壮性,通用性,效率与存储需求
9.时间复杂度和空间复杂度
第二章:线性表
1.线性表的基本操作
2.线性表的【顺序表示-链式表示】
顺序表(SqList)
3..顺序表的表定义特点插入、删除、查找
4.首位相连,可形成一个环形顺序表
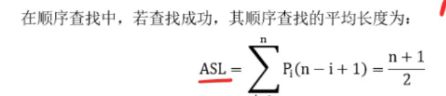
5.设顺序表的长度为n,则顺序查找的平均比较次数为(n+1)/2
链式表(LNode LinkList)
4.链式表示【单链表-循环链表-双向链表】
4.1 单链表的定义,结构描述【数据域-指针域】,建立单链表【头插法-尾插法】、单列表的查找【按序号查找结点值-按值查找表结点】、插入结点操作、删除结点操作【建表-查找-插入-删除】
4.2 循环链表
4.3 双向链表定义 、插入操作【在p之后插入-在p之前插入】、删除操作【删除P的后继S-删除结点P】【插入-删除】
第三章:栈和队列【老板-员工】
栈(Stack)-LIFO先进后出【水瓶】
1.栈和队列的共同特点-区别
2.栈的概念:栈顶、栈底、空栈
3.栈的存储结构【顺序存储结构Sqtack-链式存储结构 Link Stack】
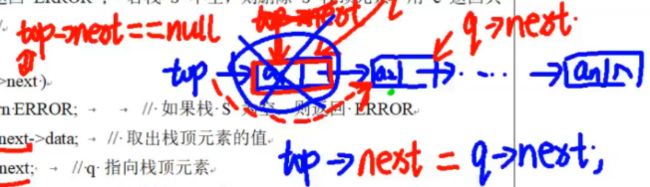
3.1 顺序栈的实现、【出栈-入栈-栈满-栈空】
初始设置S.top=-1
出栈:判断栈空;先出栈,指针再-1
3.2 链式存储概念、【入栈-出栈】
单链表有头结点
相当于链表在头节点插入,删除
队列(Queue)-FIFO先进先出【排队】
1.队列的基本概念
2.队列的存储【顺序存储-链式存储】
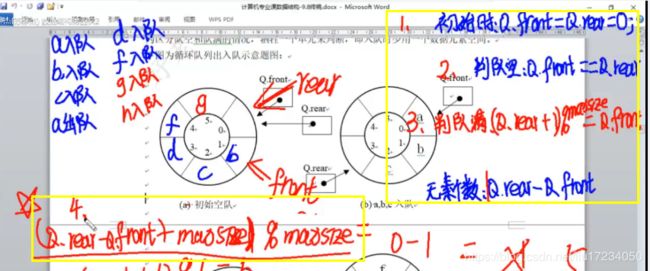
2.1 顺序存储概念、循环队列【初始时-判队空-判队满-元素个数】【入队-出队】
首尾相练形成一个环形顺序表
出队:判断队空,队头指针向前移动
2.2 链式存储概念、【出队-入队】
单链表有头结点
第四章:串【不考】
1.串的概念
2.串的存储结构
2.1 定长顺序串【串连接-求字串-定位函数】
2.2 堆分配存储表示【堆串赋值函数-求串长-串比较】
2.3 块链存储表示
第五章:数组和广义表【不考】
数组
1.二维数组的地址计算、数组的存放位置变化
2.矩阵的压缩存储【对称矩阵-三角矩阵-带状矩阵】
3.稀疏矩阵的存储概念【三元顺序表-十字链表】
广义表
1.广义表的两个基本操作【取广义表表头-取广义表表尾】
2.广义表的链式存储
第六章:树与二叉树
树
1.树的【深度-高度】
2.树的度
3.树的【分支节点-叶子结点】
二叉树
1.二叉树有左子树,右子树之分
2.特殊的二叉树【满二叉树-完全二叉树-二叉排序树-平衡二叉树】
3.【满二叉树-完全二叉树】的关系及其区别
4.二叉树的时间复杂度为:O(log2^n)
5.设二叉排序树中有n个结点,则在二叉排序树的平均平均查找长度为O(log2n)
6.在二叉排序树中插入一个结点的时间复杂度为O(n)
7.在二叉排序树中插入一个关键字值的平均时间复杂度为O(1og2n)
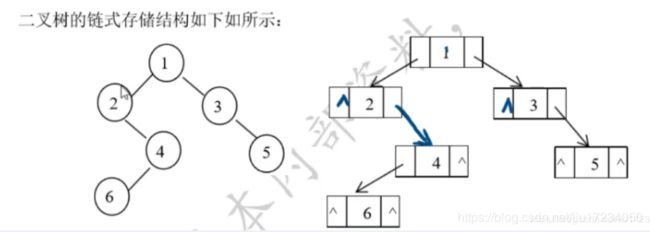
8.二叉树的存储结构【顺序存储-链式存储】
9.二叉树的遍历【先序遍历递归算法-中序遍历递归算法-后序遍历递归算法】
10.中序遍历非递归算法
线索二叉树
1.概念
2.线索化二叉树
3.画出线索二叉树
树及其转换
1.树的存储结构【双亲表示法-孩子表示法-孩子兄弟表示法】
2.【树-二叉树】的转换
3.【森林-二叉树】的转换
树与二叉树的运用
1.二叉排序树【定义、建立、查找】
2.【平衡因子-平衡二叉树(AVL树)】
3. 构造平衡二叉树的方法【法线者-麻烦结点】
哈夫曼树
1.定义
2.哈夫曼树的构造
3.哈夫曼编码
第七章:图
1.图的定义
2.【无向图-有向图-完全图】
3.顶点的度、入度、出度
4.【连通图-连通分量】
5.【强连通图-强连通分量】
6.生成树、带权图和网【稠密网、稠密图】
7.图的存储【邻阶矩阵-邻接表】
8.图的遍历【深度优先遍历(DFS)-广度优先遍历(BFS)】
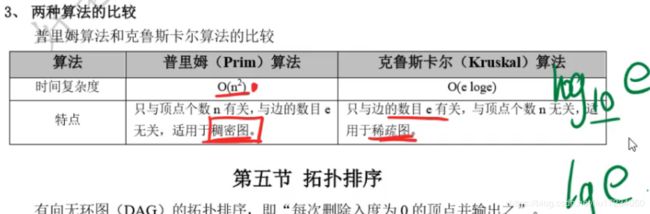
9.最小生成树构造算法【普利姆算法Prim-克鲁斯卡尔算法Kruskal】
扑克牌:一个和顶点个数有关,一个和边条数有关
10.拓扑序列
11.求最短路径的算法【迪杰斯特算法(Dijkstra)-弗洛伊德算法(Floyd)】
12.设无向图对应的邻接矩阵为A,则A中第i行上非0元素的个数___等于______第i列上非0元素的个数(填等于,大于或小于)
第八章:查找【平均查找长度的算法】
1.顺序查找
2.折半查找
3.分块查找(索引顺序查找)
4 哈希表的查找(Hash Table)
4.1 解决散列冲突的方法:开放定址法(线性探测法-二次探测法-双重散列法)-链地址法
5.装填因子
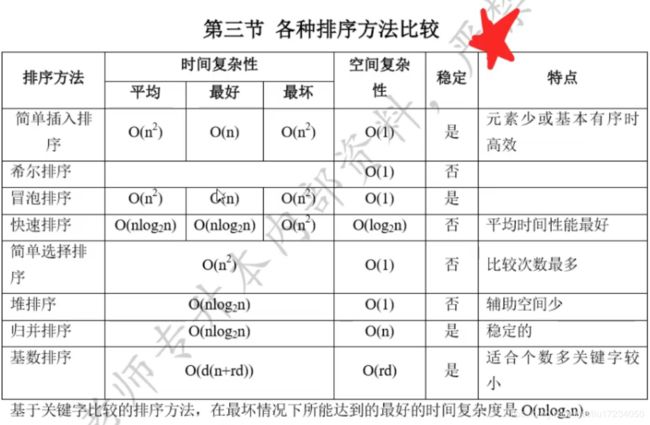
第九章:排序
1.理解各种排序怎么实现
2.代码实现
两两组合
长官说:简单查一下希尔这个罪犯,长官话冒泡的比较快
警员:很短的时间就选择了希尔的一堆犯罪记录,但是这个罪犯太狡猾没有缉拿归案,这些罪证最后归为了垃圾
简单查一下希尔这个人
冒泡比较快
简单选择就是一堆
最后归为垃圾
第一类:插入排序
直接插入排序/简单插入排序:
依次就是从第一个开始挨着下一个,对待排序序列中的每一个被插入元素进行比较,小的在前面交换顺序,然后作为一个整体,得到第一次排序结果。重复上面步骤
希尔排序:——【常考】
将序列分成几个均等部分,一半呢取一半左右分块对d3,(从前往中间依次比较:第一个和中间,第二个和中间的下一个元素,直至最后一个元素)块内呢分别进行直接插入排序,小的在前,大的在后,得到第一次排序结果。再取d2,在d1最后块间做一次直接插入排序
第二类:交换排序
冒泡排序
两个两个的比较(1和2;2和3;3和4.....依次比较),小的放前面,大的和后面一个元素个两两比较,把最大的【沉淤】到最后一个位置,这样下一次最大的不参加下一次比较,得到第一次排序结果。重复上面步骤(做n-1趟排序)
快速排序——【常考】
选一个轴值(一般选择第一个),因为轴第一次选择轴值是第一个要满足(轴值左边是小于轴值的右边是大于轴值的原则)右小左大【左——右, 选择小的;右——左,选择大的】交换,左右左右的顺序进行比较,得到第一次快速排序结果。重复上面步骤
第三类:选择排序
简单选择排序
一第一个数字为标准,依次和其他元素比较,看那个最小,把最小得数和第一个数交换位置,第一个数【沉淤】,得到第一次排序结果;
第二次从第二个数开始以第二个数为标准,依次和其他元素比较,看那个最小,把最小得数和第二个数交换位置,第二个数【沉淤】。得到第二次快速排序结果。
重复上面步骤(做n-1趟排序)
堆排序【小顶堆 -大顶堆】——【常考】
将待排序元素组成一个完全二叉树;
从第(【n/2】——这里是向下取整数)个结点开始,该结点分别与他的左右孩子比较【小顶堆:小的往上移动交换;大顶堆:大的往上移动交换】;
依次按照【n/2】-1个结点与他的左右孩子比较;
到根节点,再看其左右支树比较;
最后将第一个结点和最后一个结点交换,最后一个结点【沉淤】;得到第一次排序结果。重复上面步骤(做n-1趟排序)
第四类:归并排序——【常考】
两个和多个有序表完成,前提是子表有顺序的【块内有序,块间无序】
n个元素分成(【n/2】——这里是向下取整数)个长度为2的子序列,为奇数有一个长度为1的子序列;
从前到后两两比较合并,得到第一次排序结果。重复上面步骤;
第五类:基数排序(桶排序/数字排序)
基于多关键字排序的思路,对单逻辑关键字排除的一种内部排序算法
(比如一个三位数序列,按照个、十、百位比较得到三种排序结果)
第二部分:加强记忆注意部分
第一类:树
1.树的结点数为多少?
2.度为m的树的第i层最多有多少个结点?
3.假设树的高度为k,结点最多、最少有多少个?
4.高度为多少?
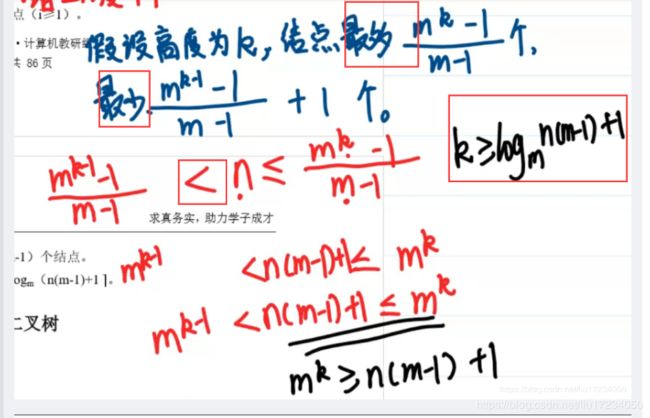
5.高度为h的m叉树至多有多少个结点?
6.n个结点的m叉树最小高度为多少?
7. n个结点的m叉树有多少个空指针域?
8.向一棵B_树插入元素的过程中,若最终引起树根结点的分裂,则新树比原树的高度__增加1____。
第二类:二叉树
1.非空二叉树上叶子结点(N0)树为多少?
2.非空二叉树,第k层上至多有多少个结点?
3.高度为h的二叉树至多有多少个结点?
4.设某棵二叉树的高度为h,则该二叉树上叶子结点最多有 2^(h-1)
5.若用链表存储一棵二叉树时,每个结点除数据域外,还有指向左孩子和右孩子的两个指针。在这种存储结构中,n个结点的二叉树共有_____2n___个指针域,其中有__n-1______个指针域是存放了地址,有_____n+1___________个指针是空指针。
第三类:完全二叉树
4.n个结点的完全二叉树的高度为多少?
5.完全二叉树是否有双亲结点-左孩子-右孩子?
6.n个结点的完全二叉树的深度为K,最多、最少有多少个结点?
7.n个结点的完全二叉树的深度为多少?
8.设一棵完全二叉树中有n个结点, 若用二叉链表作为该完全二叉树的存储结构,则共有_____n+1______个空指针域
9.设一棵完全二叉树有128(n)个结点,则该完全二叉树的深度为__8______,有____64_____(n/2)_个叶子结点
第四类:哈夫曼树【正则二叉树】
1.没有度为1的结点
2.哈夫曼树度为2的结点树为多少?
3.哈夫曼树一共有多少个结点?
度为2的n-1
度为0的n
共计n+n-1=2n-1
4.哈夫曼叶子结点(N0)树为多少?
5. 设哈夫曼树中的叶子结点总数为m,若用二叉链表作为存储结构,则该哈夫曼树中总共有2m个空指针域
空指针数=2叶子结点
6.设哈夫曼树中共有n个结点,则该树中有____(n+1)/2____个叶子结点;若采用二叉链表作为存储结构,则该树中有___(n+1)__个空指针域
每一个度为2的结点(n2)有2个空指针
用二叉链表存储时每个叶子有2个空指针域
n=no+n2 n0=n2+1 n2=no-1 n=2no-1
第五类:循环队列
1.初始时
2.判断队为空
3.判断队为满
4.判断循环队列元素个数
5.设有一个顺序循环队列中有M个存储单元,则该循环队列中最多能够存储___m-1_____个队列元素;当前实际存储___(R-F+M)%M_____________个队列元素(设头指针F指向当前队头元素的前一个位置,尾指针指向当前队尾元素的位置)
第六类:完全图
1.n个顶点的无向完全图有几条边?
在一个具有n个顶点的无向完全图中,包含有__n(n-1)/2______条边
2.n个顶点的有向完全图有几条边?
在一个具有n个顶点的有向完全图中,包含有___n(n-1)_____条边
第七类:有向图-无向图
1.有n个顶点,e条边的有向图和无向图在其对应邻接表中所含边的结点分别为多少?
对于一个具有n个顶点和e条边的有向图和无向图,在其对应的邻接表中,所含边结点分别有___e____个和____2e____个
2.设无向图中n个顶点,e条边,顶点和为d
设某无向图中顶点数和边数分别为n和e,所有顶点的度数之和为d,则e=___d/2____
3.设有向图G中有n个顶点e条有向边,所有的顶点入度数之和为d
则e和d的关系为____e=d_____
4.设某有向图中n个顶点,邻接表中有n个表头结点
5.设某有向图的邻接表中有n个表头结点和m个表结点,则该图中有m条有向边
6.设有n个结点的无向图,该图至少应有n-1条边才能确保是一个连通图
7.设无向图G中有n个顶点e条边,则其对应的邻接表中的表头结点和表结点的个数分别为 n,2e
8. 设某无向图中有n个顶点e条边,则该无向图中所有顶点的入度之和为2e
9.设某无向图G中有n个顶点,用邻接矩阵A作为该图的存储结构,则顶点i和顶点j互为邻接点的条件是
10.设无向图对应的邻接矩阵为A,则A中第i行上非0元素的个数___等于______第i列上非0元素的个数(填等于,大于或小于)
11.设无向图G中有n个顶点,则该无向图的最小生成树上有n-1条边
12.设无向图G中有n个顶点,则该无向图中每个顶点的度数最多是n-1个
第八类:连通图——强连通图
1.如果一个图有n个顶点,并且有小于n-1条边——非连通图
2.无向图的顶点数为n,则其含有全部顶点的连通图的边数最小为n-1
3.一个顶点也是强连通子图
4.当n个顶点的图构成一个环,任意两个点之间有回路(环),最小、最大边数为多少?
5.设某强连通图中有n个顶点,则该强连通图中至少有n条边