二分查找与二叉查找树

二分查找与二叉查找树

例1：二分查找

已知一个 排序数组 A，如 A = [-1, 2, 5, 20, 90, 100, 207, 800]，另外一个 乱序数组 B，如 B = [50, 90, 3, -1, 207, 80]，
求B中的任意某个元素，是否在A中出现， 结果 存储在数组C中， 出现用1 代表， 未出现用0 代表，如，C = [0, 1, 0, 1, 1, 0]。

**分析：**二分查找 又称 折半查找 ，首先，假设表中元素是按 升序排列 ，将表 中间位置 的关键字与查找关键字比较：
1.如果两者 相等 ，则 查找成功 ；
2.否则利用 中间位置 将表分成 前、后 两个子表：
1)如果中间位置的关键字 大于 查找关键字，则进一步查找 前一子表
2)否则进一步查找 后一子表
重复以上过程， 直到 找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。

例如对于待搜索数字target==2,200，数组A=[-1,2,5,20,90,100,207,800]


示例代码：

/*基于递归思路*/
bool binary_search(vector<int>&sort_array, int begin, int end, int target) {
	if (end < begin) {
		return false;
	}
	int mid = (begin + end) / 2;
	if (target == sort_array[mid]) {
		return true;
	}
	else if(target<sort_array[mid])
	{
		return binary_search(sort_array, begin, mid - 1, target);
	}
	else if (target > sort_array[mid]) {
		return binary_search(sort_array, begin + 1, mid, target);
	}
}
/*基于循环思路*/
bool binary_search(vector<int>&sort_array, int target) {
	int begin = 0;
	int end = sort_array.size() - 1;
	while (begin<=end)
	{
		int mid = (begin + end) / 2;
		if (target == sort_array[mid]) {
			return true;
		}
		else if (target < sort_array[mid]) {
			end = mid - 1;
		}
		else if(target>sort_array[mid])
		{
			begin = mid + 1;
		}
	}
	return false;
}

例2：插入位置

给定一个 排序数组nums( 无重复元素加粗样式) 与 目标值target ，如果target在nums里出现 ，则返回 target 所在下标 ，如果target在nums里 未出现 ，则返回target 应该插入位置 的数组下标，使得将target插入数组nums后，数组仍 有序 。

分析：
1.当target在nums中 出现 时，二分查找的流程无变化。
2.当target在nums 没有出现 时:
1)如果 target < nums[mid]，且target > nums[mid - 1] ；
说明了 什么？
2)如果 target > nums[mid]，且target < nums[mid + 1]；
说明了 什么？
3.当mid == 0 或者mid == nums.size() – 1时，这样的 边界条件 ，应该如何处理？

设元素 所在的位置 (或最终需要 插入的位置 )为index，
在二分查找的 过程 中:
①如果target == nums[mid]：index = mid；
②如果target < nums[mid]，且 (mid == 0或 target > nums[mid-1])：
index = mid；
③如果target > nums[mid]，且 (mid == nums.size() – 1 或 target < nums[mid+1])：
index = mid + 1；
例如：
那么，待插入的元素2此时的下标就是1，待插入的元素4的下标就是2.

示例代码：

class Solution {
public:
	int searchInsert(vector<int>&nums,int target) {
		int index = -1;
		int begin = 0;
		int end = nums.size()-1;
		while (index==-1)
		{
			int mid = (begin + end) / 2;
			if (target == nums[mid]) {
				index = mid;
			}
			else if (target < nums[mid]) {
				if (mid == 0||target > nums[mid - 1]) {
					index = mid;
				}
				end = mid - 1;
			}
			else if(target>nums[mid])
			{
				if (mid == nums.size()-1 || target < nums[mid + 1]) {//注意，这里的mid必须等于nums.size()-1，而不能等于end
					index = mid + 1;
				}
				begin = mid + 1;
			}
		}
		return index;
	}
};

例3：区间查找

给定一个 排序数组nums (nums中有 重复 元素)与 目标值target ，如果target在nums里 出现 ，则返回target所在区间的 左右端点下标 ，[左端点,右端点]，如果target在nums里 未出现 ，则返回[-1, -1]。

分析：
对于查找区间，方法一就是可以直接使用二分查找找到对应的元素，在找到相应的左右端点。
方法二就是直接找对应的左右端点。

查找区间 左端点 时，增加如下 限制条件 :
当target == nums[mid]时，若此时mid == 0或nums[mid-1] < target，则说明mid即为区间左端点，返回；否则设置查找区间右端点为mid-1。

查找区间 右端点 时，增加如下 限制条件 :
当target == nums[mid]时，若此时mid == nums.size() – 1或 nums[mid + 1] >target，则说明mid即为区间右端点；否则设置区间左端点为mid + 1

示例代码;

class Solution {
public:
	/*区间左端点*/
	int left_bound(vector<int>& nums, int target) {
		int begin = 0;
		int end = nums.size() - 1;
		while (begin<=end)
		{
			int mid = (begin + end) / 2;
			if (target == nums[mid]) {
				if (mid == 0 || target > nums[mid - 1]) {
					return mid;
				}
				end = mid - 1;
			}
			else if(target<nums[mid])
			{
				end = mid - 1;
			}
			else if(target>nums[mid])
			{
				begin = mid + 1;
			}
		}
		return -1;
	}
	
	/*区间右端点*/
	int right_bound(vector<int>&nums, int target) {
		int begin = 0;
		int end = nums.size() - 1;
		while (begin<=end)
		{
			int mid = (begin + end) / 2;
			if (target == nums[mid]) {
				if (mid==nums.size()-1||nums[mid+1]>target)
				{
					return mid;
				}
				else if(target<nums[mid])
				{
					end = mid - 1;
				}
				else if(target>nums[mid])
				{
					begin = mid + 1;
				}
			}
		}
		return -1;
	}
};

例4：旋转数组查找

给定一个 排序数组nums (nums中 无重复 元素)，且nums可能以 某个未知 下标旋转 ，给定 目标值target ，求target是否在nums中出现，若出现返回所在下标 ，未出现返回-1。

分析：
在 旋转数组 [7, 9, 12, 15, 20, 1, 3, 6]中，若 硬使用 未加修改的 二分查找，查找target = 12 或target = 3，会 出现 什么情况？
当前mid = 3，nums[mid] = 15:
查找target = 12 :target(12) < numsmid，则在子区间[7, 9, 12]中继续查找，可找到12，返回 正确 结果。
查找target = 3 :target(3) < numsmid，则在子区间[7, 9, 12]中继续查找，不可找到3，返回错误 结果。
思考：
二分查找是否还可以 继续使用 ，若希望获得正确的结果，应 如何修改 ？

修改如下：旋转数组 :[7, 9, 12, 15, 20, 1, 3, 6], nums[begin]>nums[end]
查找target = 12 时:由于target(12) < numsmid， 查找正确 的原因:
1.numsbegin < numsmid，区间[7, 9, 12, 15] 顺序递增 ，
2.target(12) > numsbegin，故target(12)只可能在顺序递增区间[7, 9, 12, 15]中。
在查找target = 3 时:由于target(3) < numsmid， 查找错误 的原因:
1.numsbegin < numsmid，区间[20, 1, 3, 6]包括 旋转 点，为 旋转区间 ，
2.target(3) < numsbegin，故target(3)可能在旋转区间[20, 1, 3, 6]中，此时忽略了该情况。
结论：
若希望使用二分查找，需要修改二分查找，将 可能在旋转区间 [20, 1, 3, 6]的情况考虑进去。

分类讨论：
情况一：
情况二：
示例代码：

class Solution {
public:
	int search(vector<int>&nums, int target) {
		int begin = 0;
		int end = nums.size() - 1;
		while (begin<=end)
		{
			int mid = (begin + end) / 2;
			if (target==nums[mid])
			{
				return mid;
			}
			else if (target < nums[mid]) {
				if (nums[begin] < nums[mid]) {//隐含着nums[begin]>nums[end]
					if (target>nums[begin])
					{
						end = mid - 1;
					}
					else
					{
						begin = mid + 1;
					}
				}
				else if(nums[begin]>nums[mid])
				{
					end = mid - 1;
				}
				else if (nums[begin] == nums[mid]) {
					begin = mid + 1;
				}
			}
			else if(target>nums[mid])
			{
				if (nums[begin] > nums[mid]) {
					begin = mid + 1;
				}
				else if (nums[begin] < nums[mid]) {
					if (target >= nums[begin]) {
						end = mid - 1;
					}
					else
					{
						begin = mid + 1;
					}
				}
				else if(nums[begin]==nums[mid])
				{
					begin = mid + 1;
				}
			}
		}
		return -1;
	}
};

二叉查找树 (Binary Search Tree), 它是一颗具有下列性质的 二叉树 :

1.若 左子树 不空，则左子树上 所有结点 的值均 小于或等于 它的 根结点 的值；
2.若 右子树 不空，则右子树上 所有结点 的值均 大于或等于 它的 根结点 的值；
3.左、右子树也分别为 二叉排序树 。
4.等于 的情况 只能出现在 左子树或右子树中的 某一侧 。

例5：二叉查找树插入节点

将 某节点(insert_node) ，插入至 以 以node 为根 二叉查找树中:
如果 insert_node节点值 小于 当前node节点值:
如果node 有左子树 ，则 递归 的将该节点插入至左子树为根二叉排序树中
否则，将 node->left 赋值 为该节点地址
否则( 大于等于 情况):
如果node 有右子树 ，则递归的将该节点插入至右子树为根二叉排序树中
否则，将 node->right 赋值 为该节点地址

示例代码:

void BST_insert(TreeNode*node, TreeNode*insert_node) {
	if (insert_node->val < node->val) {
		if (node->left) {//当左子树不为空的时候，递归的将insert_node插入左子树
			BST_insert(node->left, insert_node);
		}
		else {//当左子树为空的时候，将node的左指针与待插入节点相连接
			node->left = insert_node;
		}
	}
	else
	{
		if (node->right) {//当右子树不为空的时候，递归的将insert_node插入右子树
			BST_insert(node->right, insert_node);
		}
		else {//当右子树为空的时候，将node的右指针与待插入节点相连接
			node->right = insert_node;
		}
	}
}

例6：二叉查找树查找数值

查找 数值value 是否 在 二叉查找树 中 出现 :
如果 value 等于 当前查看node的节点值: 返回 真
如果 value节点值 小于 当前node节点值:
如果当前节点 有左子树 ， 继续 在 左子树 中查找该值；否则，返回 假
否则(value节点值 大于 当前node节点值):
如果当前节点 有右子树 ， 继续 在 右子树 中查找该值；否则，返回 假

示例代码：

bool BST_search(TreeNode*node, int value) {
	if (node->val == value) {
		return true;
	}
	else if (node->val > value) {
		if (node->left) {
			return BST_search(node->left, value);
		}
		else
		{
			return false;
		}
	}
	else
	{
		if (node->right)
		{
			return BST_search(node->right, value);
		}
		else {
			return false;
		}
	}
}

例7：二叉查找树的编码与解码

给定一个 二叉查找树 ，实现对该二叉查找树 编码与解码 功能。编码即将该二叉查找树转为 字符串 ，解码即将字符串转为 二叉查找树 。不限制使用何种编码算法，只需 保证 当对二叉查找树调用编码功能后可再调用解码功能将其 复原 。

分析：
对 二叉查找树 进行 前序遍历 ，将遍历得到的结果按顺序 重新构造 为一颗 新的 二叉查找树，新的二叉查找树与原二叉查找树 完全一样 。现在唯一的不同就是在数据，在遍历的过程中要加上编码的过程，在构造二叉树的时候要加上解码的过程。
①对于编码而言：
二叉查找树 编码 为字符串:将二叉查找树 前序遍历 ，遍历时将 整型的数据转为字符串 ，并将这些字符串数据 进行连接 ，连接时使用 特殊符号 分隔。

②对于解码而言：
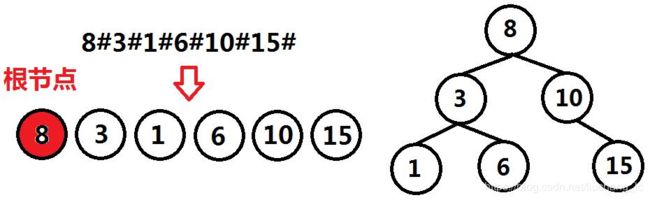
将字符串 解码 为二叉查找树:将字符串按照编码时的 分隔符”#” ，将各个数字 逐个拆分 出来，将 第一个数字 构建为二叉查找树的 根节点 ，后面各个数字构建出的节点按解析时的顺序 插入根节点中，返回根节点，即完成了 解码 工作。
我们注意到：对于一般的二叉树而言，要根据数组或者字符串重构二叉树，至少需要两种遍历序列，才能正确还原二叉树，但是对于二叉查找树来说，根据前序遍历序列加上二叉查找树的性质就能还原一颗二叉查找树。

示例代码：

class Solution {
public:
	/*整型转字符串*/
	void  change_int_to_string(int val, string &str_val) {
		string temp;
		while (val)//int转string
		{
			temp = val % 10 + '0';
			val = val / 10;
		}
		for (int  i = temp.size(); i >=0; i--)//将字符串倒置
		{
			str_val += temp[i];
		}
		str_val += '#';//以‘#’作为节点的分隔符
	}

	/*二叉查找树的前序遍历*/
	void BST_preorder(TreeNode*node, string &data) {//注意要使用引用
		if (!node) {
			return;
		}
		string str_val;
		change_int_to_string(node->val, str_val);//int 转string
		data += str_val;
		BST_preorder(node->left, data);
		BST_preorder(node->right, data);
	}

	/*二叉查找树的反序列化*/
	TreeNode*depreorder(string data) {
		if (data.length()==0)
		{
			return nullptr;
		}
		vector<TreeNode*>node_vec;
		int val = 0;
		for (int i = 0; i < data.length(); i++)
		{
			if (data[i]=='#')//以字符串‘#’作为分隔
			{
				node_vec.push_back(new TreeNode(val));
				val = 0;//val记录的是字符串转为int的值，每转换完一个数，就将val置0
			}
			else
			{
				val = val * 10 + data[i] - '0';//字符串转int
			}
		}
		for (int  i = 0; i < node_vec.size(); i++)
		{
			BST_insert(node_vec[0], node_vec[i]);//插入二叉查找树
		}
		return node_vec[0];
	}
};