机器学习第七周 逻辑回归

机器学习第七周 逻辑回归

1 学习目标

知识点描述：应用广泛的二分类算法——逻辑回归

学习目标：

• 逻辑回归本质及其数学推导
• 逻辑回归代码实现与调用
• 逻辑回归中的决策边界、多项式以及正则化

2 学习内容

《出场率No.1的逻辑回归算法，是怎样“炼成”的？》

《逻辑回归的本质及其损失函数的推导、求解》

《逻辑回归代码实现与调用》
《逻辑回归的决策边界及多项式》

《sklearn中的逻辑回归中及正则化》

3 学习ing

之前学习过了线性回归linearRegression ,现在开始学习逻辑回归logistic Regression (LR)。

原理：将样本的特征和样本发生的概率联系起来，即预测的是样本发生的概率。
KaTeX parse error: Unknown column alignment: 1 at position 38: …begin{array}{rc1̲} 0 & \hat{p}\l…
类似上面概率范围确定非线性结果变换。

自变量集合
$$X=（x_1,x_2,...,x_k,1）$$
这些参数表示这种特征，决定用户的一种行为，正效应用y*和负效应y~表示。客户的购买行为记为y,其中y=1表示会购买；y=0表示没有购买。于是公式如下：
KaTeX parse error: Unknown column alignment: 1 at position 44: …begin{array}{rc1̲} 1 & y*\gt y~\…
如果假设正负效应函数与自变量特征参数成线性相关，则根据简单线性回归y=ax+b得出，
$$y\ast =X_i\phi +{\theta }_i,y=X_i\omega +{\tau }_i,其中{\theta }_i,{\tau }_i是相互独立的随机变量，且都服从正态分布。$$
在得到正负效应线性函数之后，就可以用正效应减去负效应的解是否大于0作为分类的依据。
$$z_i=y\ast -y,\gamma =\phi -\omega ,\epsilon =\theta -\tau ;z=X\gamma +\epsilon$$

$$P(z=1)=p(X\gamma +\epsilon >0)=p(\epsilon >-X\gamma )=1-p(\epsilon -\le X\gamma )=1-F_e(-X\gamma )$$

$$Fe是随机变量\epsilon 的累积分布函数$$

使用标准逻辑分布的累积分布函数
$$\sigma (t)来替换正态分布的累积分布函数F_{\epsilon }(t)$$

$$标准逻辑分布的概率密度函数为f(x)=\frac{e^{-x}}{(1+e^{-x}{)}^2}$$

对应的积累分布函数为：
$$\sigma (t)=\frac{1}{1+e^{-t}}$$

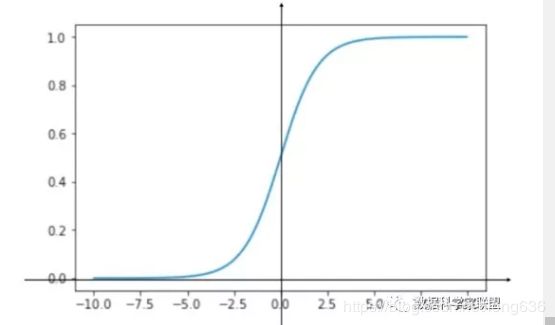
将线性回归模型带入到sigmoid中，当t>0是其结果概率为p>0.5;反之t<0,p<0.5.因此：
$$\hat{p}=\sigma ({\theta }^T.X_b)=\frac{1}{1+e^{-{\theta }^T.X_b}}$$

逻辑回归其中思想：对问题划分层次，并利用非线性变换和线性模型的组合，将未知的复杂的问题分解为已知的简单问题。

逻辑回归假设数据服从伯努利分布，通过极大似然函数的方法，运用梯度下降来求解参数，来将数据进行二分类的目的。？？？

逻辑回归推导过程：

逻辑回归，这里利用了线性回归理论做支撑，并对回归做了对数变换，可以称为“对数线性回归”：
$$ln(y)={\theta }^T.X_b,则y=e^{{\theta }^T.X_b},这里做了空间变换$$
这个函数是可求导的，因此也是连续的。sigmoid函数的区间范围也是在（0，1），可以近似逼近真实值。

逻辑回归模型：
KaTeX parse error: Unknown column alignment: 1 at position 89: …begin{array}{rc1̲} 1 & \hat{p}\g…
在线性回归中，求解未知参数的做法是：
$$已知{\theta }^T.x_b估计值，用估计值与真值的差来度量结果的好坏，利用MSE（差值的平方和再求平均）作为损失函数，通过导数求极值的方法找到令损失函数最小的\theta$$
逻辑回归中的思路是：

针对逻辑回归解决分类问题，得到y是1，0的结果。估算出来的概率p来决定结果值。这里将损失函数分为两类，
给定样本是y=1,估计出来的概率p

给定样本是y=0,估计出来的概率是p
KaTeX parse error: Unknown column alignment: 1 at position 27: …begin{array}{rc1̲} -log(\hat{p})…
通过一种巧妙的方法构造单个样本的误差：
$$J（\hat{p},y）=-log({\hat{p}}^y)-log(1-\hat{p}{)}^{1-y}$$
因此对整个集合内的损失取平均值：（按照线性回归方式）
$$J(\theta )=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}log(\hat{p}{)}^y+(1-y^{(i)})log(1-{\hat{p}}^{(i)})]$$
再将替换成sigmoid函数，得到逻辑损失函数如下：
$$J(\theta )=-\frac{1}{m}\sum _{i=1}^m\{y^{(i)}log(\sigma ({\theta }^T.X_b^{(i)}))+(1-y^{(i)})log(1-\sigma ({\theta }^T.X_b^{(i)}]))\}$$
该损失函数是没有标准方程解的，在实际使用过程中使用梯度下降来不断逼近最优解。

计算梯度，函数对参数进行求偏导数，
$$▽f=(\frac{\partial L(\theta )}{\partial {\theta }_0},\frac{\partial L(\theta )}{\partial {\theta }_1},...,\frac{\partial L(\theta )}{\partial {\theta }_n}{)}^T$$
根据链式求导法则：
$$\sigma (t)=(1+e^{-t}{)}^{-1},{\sigma }^{\prime }(t)=-1(1+e^{-t}{)}^{-2}(-e^{-t})=\frac{e^{-t}}{(1+e^{-t}{)}^2}$$
外层：
$$(log(\sigma (t)){)}^{\prime }=\frac{1}{\sigma (t)}{\sigma }^{\prime }(t)$$
得到：
$$（log\sigma (t){）}^{\prime }=\frac{e^{-t}}{(1+e^{-t})}=1-\sigma (t)$$
因此前半部分的求导得：
$$y^{(i)}(1-\sigma ({\theta }^T.X_b^{(i)}))X_b^{(i)}$$
后半部分的求导：
$$（1-y^{(i)}）\frac{-1}{1-\sigma ({\theta }^T.X_b^{(i)})}(\sigma (t)-{\sigma }^2(t))X_b^{(i)}=$$

$$-(1-y^{(i)})\sigma ({\theta }^T.X_b^{(i)})X_b^{(i)}$$

最终两者结果相结合
$$\frac{L(\theta )}{{\theta }_j}=\frac{1}{m}\sum _{i=1}^m(y^{(i)}-\sigma ({\theta }^T.X_b^{(i)}))X_j^{(i)}$$
最终（注：前面有个负号）
$$▽J(\theta )=\frac{1}{m}{X}_b^T(\sigma (X_b\theta )-y)$$
逻辑回归代码实现与调用：

#逻辑回归，先定义sigmoid函数
#定义损失函数，使用梯度下降得到参数
#参数带入回归模型，得到概率，概率再转化为分类
import numpy as  np
#对评价指标进行更改
#from metrics import accuracy_score
from sklearn.metrics import accuracy_score

class LogisticRegression:
    
    def __init__(self):
        '''初始化逻辑回归模型'''
        self.coef_ = None
        self.intercept_ = None
        self._theta = None
        
    '''定义sigmoid函数'''
    def sigmoid(self,t):
        return 1./(1. + np.exp(-t))
    
    '''
    fit方法，使用梯度下降训练法训练logstic regression模型
    参数：训练数据集X_train,y_train,学习率，迭代次数
    输出：训练好的模型
    '''
    def fit(self, X_train, y_train, eta=0.01, n_iters = 1e4):
        
        assert X_train.shape[0] == y_train.shape[0],"x_train 和y_train行维度相同"
        
        '''
        定义逻辑回归的损失函数
        参数：theta ,构造好的矩阵X_b,标签y
        输出：损失函数表达式
        '''
        def J(theta, X_b, y):
            #定义逻辑回归模型y_hat
            y_hat = self.sigmoid(X_b.dot(theta))
            try:
                #返回损失函数
                return -np.sum(y*np.log(y_hat)+(1-y)*np.log(1-y_hat))/len(y)
            except:
                return  float('inf')
            
        '''
        损失函数的导数计算
        参数：theta,X_b,标签y
        输出：计算的表达式
        '''
        def dJ(theta,X_b,y):
            return X_b.T.dot(self.sigmoid(X_b.dot(theta))- y) / len(y)
        
        '''梯度下降计算的过程'''
        def gradient_descent(X_b,y,initial_theta, eta, n_iters = 1e4, epsilon = 1e-8):
            theta = initial_theta
            curr_iter = 0
            while curr_iter < n_iters:
                gradient = dJ(theta, X_b, y)
                last_theta = theta
                theta = theta - eta * gradient
                #theta = theta - eta / (1 + np.exp(-curr_iter)) * gradient 
                if (abs(J(theta,X_b,y) -J(last_theta,X_b,y)) < epsilon):
                    break
                curr_iter += 1
            return theta
        
        X_b = np.hstack([np.ones((len(X_train),1)), X_train])
        initial_theta = np.zeros(X_b.shape[1])
        
        #梯度下降的结果求出参数theta
        self._theta = gradient_descent(X_b,y_train,initial_theta,eta,n_iters)
        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]
        
        return self
    '''
    逻辑回顾预测，根据概率进行分类，因此先预测概率
    参数：输入空间X_predict
    输出：结果概率向量
    '''
    def predict_proba(self,X_predict):
        assert self.intercept_ is not None and self.coef_ is not None ,"先进行训练"
        assert X_predict.shape[1] == len(self.coef_) , "预测的维度应该相同"
        X_b = np.hstack([np.ones((len(X_predict),1)),X_predict])
        return self.sigmoid(X_b.dot(self._theta))
    '''
    使用X_predict的结果概率向量，将其转换为分类
    参数：X_predict
    输出：分类结果
    '''
    def predict(self,X_predict):
        assert self.intercept_ is not None and self.coef_ is not None ,"先进行训练"
        assert X_predict.shape[1] == len(self.coef_) , "预测的维度应该相同"
        #得到概率
        proba = self.predict_proba(X_predict)
        #判断概率是否大于0.5，利用布尔表达式处理
        return np.array(proba >= 0.5 , dtype='int')
    def score(self,X_test,y_test):
        y_predict = self.predict(X_test)
        return  accuracy_score(y_test,y_predict)
    
    def __repr__(self):
        return  "Logistic Regression()"

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
X = X[y<2, :2]
y = y[y<2]
plt.scatter(X[y==0,0],X[y==0,1], color='red')
plt.scatter(X[y==1,0],X[y==1,1], color='blue')
plt.show()

#调用测试
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
# 查看训练数据集分类准确度
log_reg.score(X_test, y_test)
# 1.0 

log_reg.predict_proba(X_test)
#array([0.93292947, 0.98717455, 0.15541379, 0.01786837, 0.03909442,
       0.01972689, 0.05214631, 0.99683149, 0.98092348, 0.75469962,
       0.0473811 , 0.00362352, 0.27122595, 0.03909442, 0.84902103,
       0.80627393, 0.83574223, 0.33477608, 0.06921637, 0.21582553,
       0.0240109 , 0.1836441 , 0.98092348, 0.98947619, 0.08342411])

log_reg.predict(X_test)
#array([1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0,
       1, 1, 0])

决策边界：

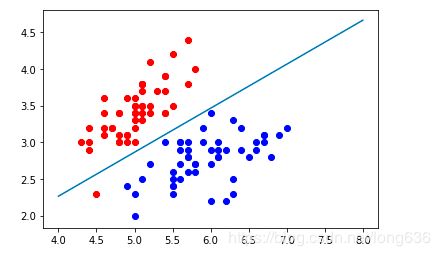
逻辑回归分类思想：通过训练的方式求出一个n+1维的向量，每当新来一个样本x_b时，与n+1维向量进行点乘，结果带入sigmoid函数，得到的值为该样本发生在定义y_hat=1 事件的概率值。如果概率大于0.5，分类为1，否则为0.
$$\hat{p}=\sigma (t)=\frac{1}{1+e^{-t}},t={\theta }^T.x_b$$

$$当t>0,1<1+e^{-t}<2,则0.5<\hat{p}<1;当t<0，1+e^{-t}>2,则\hat{p}<0.5$$

$$有一个边界点{\theta }^T.x_b=0,大于这个边界点，分类为1，小于这个边界点分类为0；称之为决策边界decisionboundary.$$

假设X有两个特征x1,x2,那么有：
$${\theta }^T.x_b={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2=0，这是一条直线，那么这条直线就是分界线$$

$$x2=\frac{-{\theta }_0-{\theta }_1{x}_1}{{\theta }_2}$$

def x2(x1):
    return  (-log_reg.intercept_-log_reg.coef_[0]* x1) /log_reg.coef_[1]

x1_plot = np.linspace(4,8,1000)
x2_plot = x2(x1_plot)
plt.scatter(X[y==0,0],X[y==0,1],color='red')
plt.scatter(X[y==1,0],X[y==1,1],color='blue')
plt.plot(x1_plot,x2_plot)
plt.show()

这条直线就是决策边界，新来的点在直线上方分类为0，在直线下方分类为1.因此可以看出线性决策边界是一条直线，如果是多项式，则使分类算法的决策边界不在规律。

决策边界就是能够把样本正确分类的一条边界，主要有线性决策边界linear decision boundaries和非线性决策边界non-linear decision bundaries。

对于非线性逻辑回归，可以使用线性回归计算非线性时所采用的的方法，高次项看做是一个特征，转换成线性回归。

对于复杂的问题是需要使用多项式，但多项式的阶数越大，越容易过拟合。因此需要进行模型的正则化。

对损失函数增加L1正则或L2正则。可以引入参数a来调节损失函数和正则项的权重。如：
$$J(\theta )+\alpha L1;C.J(\theta )+L1$$

from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

def PolynomialLogisticRegression(degree):
    return Pipeline([
        ('poly', PolynomialFeatures(degree=degree)),
        ('std_scaler', StandardScaler()),
        ('log_reg', LogisticRegression())
    ])

poly_log_reg = PolynomialLogisticRegression(degree=2)
poly_log_reg.fit(X_train, y_train)

这里又使用了pipeline

Pipeline(memory=None,
         steps=[('poly',
                 PolynomialFeatures(degree=2, include_bias=True,
                                    interaction_only=False, order='C')),
                ('std_scaler',
                 StandardScaler(copy=True, with_mean=True, with_std=True)),
                ('log_reg',
                 LogisticRegression(C=1.0, class_weight=None, dual=False,
                                    fit_intercept=True, intercept_scaling=1,
                                    l1_ratio=None, max_iter=100,
                                    multi_class='auto', n_jobs=None,
                                    penalty='l2', random_state=None,
                                    solver='lbfgs', tol=0.0001, verbose=0,
                                    warm_start=False))],
         verbose=False)

参数C 和L2

在实际使用中，阶数degree,参数C以及正则化项，都是超参数，使用网格搜索的方式得到最佳组合。