Stacked Autoencoders学习笔记

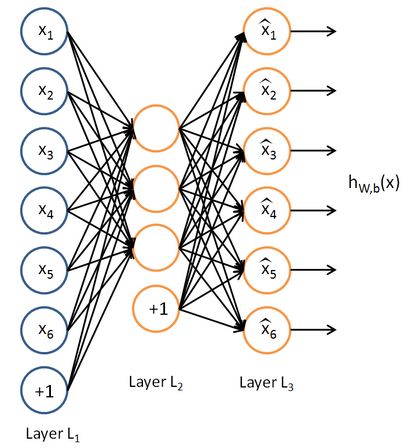
上图是一个栈式自编码算法模型，属于无监督学习。栈式自编码神经网络是一个由多层自编码器组成的神经网络，其前一层自编码器的输出作为其后一层自编码器的输入。通过将重构的x与输入的x相减来计算误差。
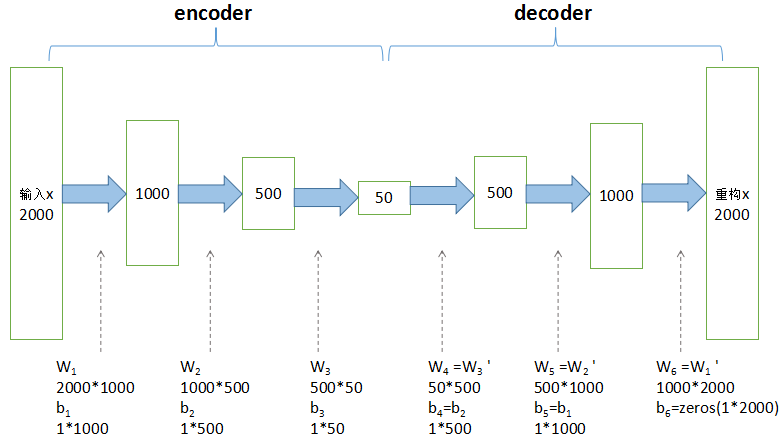
encoder部分从原始2000维特征降至50维（根据实际情况，自定义特征数），有三个隐层，每一层都是提取的高维特征，最后一层作为降维后的特征可用作分类和回归。decoder部分输出重构的x，通过调整encoder和decoder的参数，使得重构误差最小。

含有一个隐层的AE模型

栈式自编码算法代码解读
代码来源：Matlab Toolbox for Dimensionality Reduction

function [model, mappedX] = train_deep_autoenc(X, layers, lambda)
%TRAIN_DEEP_AUTOENC Trains a deep feedforward autoencoder on X
%X是原始数据集，NxD。layers是一维数组，存放每层降维的特征数，按上述图中，则是[1000 500 50]。lambda是L2规则项的系数（默认为0），

    if ~exist('lambda', 'var') || isempty(lambda)
        lambda = 0;
    end

    % Pretrain model using stacked denoising auto-encoders
    no_layers = length(layers);%encoder的层数，上述图片中是3层
    model = cell(2 * no_layers, 1);%初始化SAE模型，6层
    mappedX = X;
    for i=1:no_layers  %预训练encoder部分的参数W和b
        noise = 0.1;
        max_iter = 30;
        [network, mappedX] = train_autoencoder(mappedX, layers(i), noise, max_iter);%传入每一个隐层的特征数
        model{i}.W        = network{1}.W;
        model{i}.bias_upW = network{1}.bias_upW;
        %将得到的network中的encoder的系数存入model
    end

    for i=1:no_layers %将model中encoder的参数赋给decoder
        model{no_layers + i}.W        = model{no_layers - i + 1}.W';将encoder的W'赋给对应decoder的W
        if i ~= no_layers
            model{no_layers + i}.bias_upW = model{no_layers - i}.bias_upW;将encoder的b赋给对应decoder的b
        else
            model{no_layers + i}.bias_upW = zeros(1, size(X, 2));%decoder最后一层的b初始化为0
        end
    end
    clear network mappedX


    % Compute mean squared error of initial model predictions
    reconX = run_data_through_autoenc(model, X);
    disp(['MSE of initial model: ' num2str(mean((reconX(:) - X(:)) .^ 2))]);

    % Finetune model using gradient descent
    noise = 0.1;
    max_iter = 30;
    model = backprop(model, X, X, max_iter, noise, lambda);

    % Compute mean squared error of final model predictions
    [reconX, mappedX] = run_data_through_autoenc(model, X);
    disp(['MSE of final model: ' num2str(size(X, 2) .* mean((reconX(:) - X(:)) .^ 2))]);
end

function [network, mappedX, reconX] = train_autoencoder(X, layers, noise, max_iter)
%TRAIN_AUTOENCODER Trains an simple autoencoder
%mappedX是低维特征

    if nargin < 2
        error('Not enough inputs.');
    end
    if isempty(layers)
        error('There should be at least one hidden layer.');%至少有一个隐层
    end
    if ~exist('noise', 'var') || isempty(noise)
        noise = 0;
    end
    if ~exist('max_iter', 'var') || isempty(max_iter)
        max_iter = 50;
    end

    % Initialize the network
    D = size(X, 2);%输入特征的维数
    no_layers = length(layers) + 1;
    network = cell(no_layers, 1);%初始化含有一个隐层的AE模型
    %初始化第一层系数W和b
    network{1}.W = randn(D, layers(1)) * .0001;
    network{1}.bias_upW = zeros(1, layers(1));
     %初始化中间层系数W和b
    for i=2:no_layers - 1
        network{i}.W = randn(layers(i - 1), layers(i)) * .0001;
        network{i}.bias_upW = zeros(1, layers(i));
    end
    %初始化最后一层系数W和b
    network{no_layers}.W = randn(layers(end), D) * .0001;
    network{no_layers}.bias_upW = zeros(1, D);

    % 计算重构误差
    reconX = run_data_through_autoenc(network, X);
    disp(['Initial MSE of reconstructions: ' num2str(mean((X(:) - reconX(:)) .^ 2))]);    

    % Perform backpropagation to minimize reconstruction error
    network = backprop(network, X, X, max_iter, noise);
    %得到更新系数后的network（包括encoder和decoder的系数），并返回network 

    % Get representation from hidden layer
    [reconX, mappedX] = run_data_through_autoenc(network, X);
    disp(['Final MSE of reconstructions: ' num2str(mean((X(:) - reconX(:)) .^ 2))]);

function [reconX, mappedX] = run_data_through_autoenc(network, X)
%RUN_DATA_THROUGH_AUTOENC Intermediate representation and reconstruction
%
%  将输入X通过network（encoder和decoder）计算，得到重构X

    % Initialize some variables
    n = size(X, 1);
    no_layers = length(network);
    middle_layer = ceil(no_layers / 2);%得到中间隐层数（encoder的最后一层）

    % Run data through autoencoder
    activations = [X ones(n, 1)];
    for i=1:no_layers
        if i ~= middle_layer && i ~= no_layers
        %非中间层和最后一层，都用sigmoid函数，得到数值在0~1之间
            activations = [1 ./ (1 + exp(-(activations * [network{i}.W; network{i}.bias_upW]))) ones(n, 1)];
        else
        %中间层和最后一层，得到的数据用在预测和重构误差，不需要在0~1之间
            activations = [activations * [network{i}.W; network{i}.bias_upW] ones(n, 1)];
            if i == middle_layer
                mappedX = activations(:,1:end-1);%中间隐层得到的特征就是降维特征，返回mappedX 用于分类和回归
            end
        end
    end
    reconX = activations(:,1:end-1);%最后一层是重构误差X

其中，activations * [network{i}.W; network{i}.bias_upW] 就是