吴恩达机器学习 EX3 作业 第一部分多分类逻辑回归 手写数字

1 多分类逻辑回归

逻辑回归主要用于分类，也可用于one-vs-all分类。如本练习中的数字分类，输入一个训练样本，输出结果可能为0-9共10个数字中的一个数字。一对多分类训练过程使用“一对余”方法，如训练一个样本，判断是否为1时。1是正类，其余数字均为负类。

1.1 导入模块和数据

import matplotlib.pyplot as plt
import numpy as np
import scipy.io as scio
import scipy.optimize as opt

import displayData as dd # 绘制数字图形函数
import lrCostFunction as lCF # 逻辑回归代价函数，单分类和多分类代价函数相同
import oneVsAll as ova # 一对多分类函数
import predictOneVsAll as pova # 预测函数

初始化数据

plt.ion()
# Setup the parameters you will use for this part of the exercise
input_layer_size = 400  # 20x20 input images of Digits
num_labels = 10         # 10 labels, from 0 to 9
                        # Note that we have mapped "0" to label 10

加载数据，X是5000个手写数字集，每个手写数字被压缩成20*20像素灰度图片的浮点数值格式，当然每个数字被展开成一行400个浮点数值
因变量y是每个数字集对应的实际数字(0-9)，不过此处0被转换成10存储，1-9保持不变，即y取值范围为(1-10)

data = scio.loadmat('ex3data1.mat')
X = data['X']
y = data['y'].flatten()
m = y.size

打印X， y维度

print('X.shape: ', X.shape, '\ny.shape: ', y.shape)

X.shape:  (5000, 400) 
y.shape:  (5000,)

显示y，y为5000条1到10的数值，其中10表示数字0

y

array([10, 10, 10, ...,  9,  9,  9], dtype=uint8)

显示一个训练样本部分数据

X[2][90:100]

array([ 0.000483, -0.005167, -0.015521, -0.016165, -0.016218, -0.016096,
       -0.005737,  0.000682,  0.000000,  0.000000])

1.2 绘制数字图片函数(displayData.py)

import matplotlib.pyplot as plt
import numpy as np

def display_data(x):
    (m, n) = x.shape # 训练样本维度 (100, 400)
    # Set example_width automatically if not passed in
    example_width = np.round(np.sqrt(n)).astype(int) # 数字图片宽 20
    example_height = (n / example_width).astype(int) # 数字图片高 20
    # Compute the number of items to display
    display_rows = np.floor(np.sqrt(m)).astype(int) # 训练样本行数：10
    display_cols = np.ceil(m / display_rows).astype(int) # 训练样本列数：10 
    # Between images padding
    pad = 1 # 数字图片前后左右间隔为1px
    # Setup blank display 显示样例图片范围
    display_array = - np.ones((pad + display_rows * (example_height + pad),
                              pad + display_rows * (example_height + pad)))
    # Copy each example into a patch on the display array
    curr_ex = 0
    for j in range(display_rows):
        for i in range(display_cols):
            if curr_ex > m:
                break
            # Copy the patch
            # Get the max value of the patch
            max_val = np.max(np.abs(x[curr_ex]))#不明白为啥要除最大值，没看出差异
            # 开始一个个画出数字图
            display_array[pad + j * (example_height + pad) + np.arange(example_height),
                          pad + i * (example_width + pad) + np.arange(example_width)[:, np.newaxis]] = \
                          x[curr_ex].reshape((example_height, example_width)) / max_val
            curr_ex += 1

        if curr_ex > m:
            break

    # Display image
    plt.figure()
    plt.imshow(display_array, cmap='gray', extent=[-1, 1, -1, 1])
    plt.axis('off')

随机选择100数字图，并显示效果<\b>

# Randomly select 100 data points to display
rand_indices = np.random.permutation(range(m))
selected = X[rand_indices[0:100], :]

dd.display_data(selected)

1.3 sigmoid函数

sigmoid函数为逻辑回归激活函数，根据将输入数据将输出数据控制在0～1范围内
sigmoid公式：

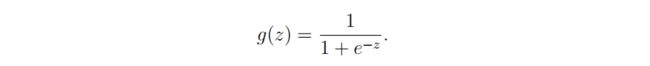
def sigmoid(z):
    g = 1 / (1 + np.exp(-z))
    return g

1.4 逻辑回归代价函数(lrCostFunction.py)

介绍部分详见 吴恩达机器学习 EX2 作业 第二部分正则化逻辑回归

def lr_cost_function(theta, X, y, lmd):
    m = y.size
    cost = 0
    grad = np.zeros(theta.shape)
	#逻辑回归假设函数
    hypothesis = sigmoid(np.dot(X, theta))
    #由于正则化不包含theta0，剔除theta0参数
    reg_theta = theta[1:]
    # 含正则化的代价函数
    cost = np.sum(-y * np.log(hypothesis) - (1 - y) * np.log(1 - hypothesis)) / m + (lmd / (2 * m)) * np.sum(reg_theta * reg_theta)
    # 梯度下降，不含正则化
    normal_grad = (np.dot(X.T, hypothesis - y) / m).flatten()

    grad[0] = normal_grad[0]
    #对批量题库下降除theta0外部分参数进行正则化处理
    grad[1:] = normal_grad[1:] + reg_theta * (lmd / m)

    return cost, grad

1.5 测试验证逻辑回归代价函数

theta_t = np.array([-2, -1, 1, 2])
X_t = np.c_[np.ones(5), np.arange(1, 16).reshape((3, 5)).T/10]
y_t = np.array([1, 0, 1, 0, 1])
lmda_t = 3

显示输入数据

X_t

array([[1. , 0.1, 0.6, 1.1],
       [1. , 0.2, 0.7, 1.2],
       [1. , 0.3, 0.8, 1.3],
       [1. , 0.4, 0.9, 1.4],
       [1. , 0.5, 1. , 1.5]])

y_t

array([1, 0, 1, 0, 1])

cost, grad = lr_cost_function(theta_t, X_t, y_t, lmda_t)
np.set_printoptions(formatter={'float': '{: 0.6f}'.format})
print('Cost: {:0.7f}'.format(cost))
print('Expected cost: 2.534819')
print('Gradients:\n{}'.format(grad))
print('Expected gradients:\n[ 0.146561 -0.548558 0.724722 1.398003]')

Cost: 2.5348194
Expected cost: 2.534819
Gradients:
[ 0.146561 -0.548558  0.724722  1.398003]
Expected gradients:
[ 0.146561 -0.548558 0.724722 1.398003]

1.6 一对多分类函数(oneVsAll.py)

def one_vs_all(X, y, num_labels, lmd):
    # Some useful variables
    (m, n) = X.shape

    # You need to return the following variables correctly
    all_theta = np.zeros((num_labels, n + 1))

    # Add ones to the X data 2D-array
    X = np.c_[np.ones(m), X]
    print(X.shape)
    
    def cost_func(t):
        return lr_cost_function(t, X, y_i, lmd)[0]

    def grad_func(t):
        return lr_cost_function(t, X, y_i, lmd)[1]

    for i in range(1, num_labels+1):
        print('Optimizing for handwritten number {}...'.format(i))

        initial_theta = np.zeros((n + 1, 1))
        # iclass = i if i else 10 # 数字1-9不变，数字0转成10
        # “一对余”算法，如当训练数字1时，其余数字均置为0
        y_i = np.array([1 if j == iclass else 0 for j in y])

        def cost_func(t):
            return lr_cost_function(t, X, y_i, lmd)[0]

        def grad_func(t):
            return lr_cost_function(t, X, y_i, lmd)[1]
		# 用高级优化更新参数theta
        theta, *unused = opt.fmin_cg(cost_func, fprime=grad_func, x0=initial_theta, maxiter=100, disp=False, full_output=True)
        print('Done')
        all_theta[i] = theta
        

    return all_theta

调用one_vs_all更新theta

lmd = 0.1
all_theta = one_vs_all(X, y, num_labels, lmd)

(5000, 401)
Optimizing for handwritten number 0...
Done
Optimizing for handwritten number 1...
Done
Optimizing for handwritten number 2...
Done
Optimizing for handwritten number 3...
Done
Optimizing for handwritten number 4...
Done
Optimizing for handwritten number 5...
Done
Optimizing for handwritten number 6...
Done
Optimizing for handwritten number 7...
Done
Optimizing for handwritten number 8...
Done
Optimizing for handwritten number 9...
Done

1.7 预测函数(predictOneVsAll.py)

def predict_one_vs_all(all_theta, X):
    m = X.shape[0]
    # all_theta.shape (10, 401)
    num_labels = all_theta.shape[0] 
 
    # You need to return the following variable correctly;
    p = np.zeros(m)

    # Add ones to the X data matrix
    X = np.c_[np.ones(m), X] # (5000, 401)

    rs = np.dot(all_theta, X.T)
    rs = np.roll(rs, -1, axis=0) # 将第一行移到最后一行
    rs = np.vstack([np.zeros(m), rs]) # 增加一行，全部为0的值
    p = np.argmax(rs, axis=0)
    
    rs = sigmoid(np.dot(X, all_theta.T)) # 通过假设函数计算预测结果 (5000, 10)
    # one_vs_all函数更新的theta参数时预测数字转换成10，预测的数据还是0。theta0预测的值通过np.roll函数换到最后
    rs = np.roll(rs, -1, axis=1)
    # 所有预测结果前增加为0的值，假设函数计算结果在[0-9]之间，所以结算结果列都加0通过np.argmax取得位置在[1-10]之间
    rs = np.hstack([np.zeros(m)[:, np.newaxis], rs])
    p = np.argmax(rs, axis=1)

    return p

1.8 调用预测函数预测结果

预测结果还行，通过学习曲线可以找到更合适的参数theta，后续课程中有关于学习曲线部分内容，到时尝试处理

pred = predict_one_vs_all(all_theta, X)

print('Training set accuracy: {}'.format(np.mean(pred == y)*100))

Training set accuracy: 91.46

前一篇 吴恩达机器学习 EX2 作业 第二部分正则化逻辑回归
后一篇 吴恩达机器学习 EX3 作业 第二部分神经网络 前向传播 手写数字