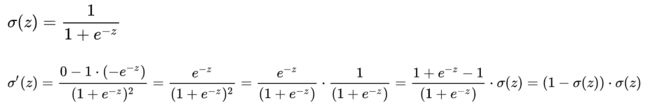常用激活函数总结
激活函数总结
- 1. Sigmoid
- 2. tanh
- 3. ReLU
- 4. LeakyReLU, PReLU（Parametric Relu）, RReLU
- 5. GELU
- 5. softmax
写在前面：
- 神经网络为什么需要激活函数： 首先数据的分布绝大多数是非线性的，而一般神经网络的计算是线性的，引入激活函数，是在神经网络中引入非线性，强化网络的学习能力。所以激活函数的最大特点就是非线性。
- 不同的激活函数，根据其特点，应用也不同。 Sigmoid和tanh的特点是将输出限制在(0,1)和(-1,1)之间，说明Sigmoid和tanh适合做概率值的处理，例如LSTM中的各种门；而ReLU就不行，因为ReLU无最大值限制，可能会出现很大值。同样，根据ReLU的特征，Relu适合用于深层网络的训练，而Sigmoid和tanh则不行，因为它们会出现梯度消失。
- 在使用relu的网络中，是否还存在梯度消失的问题？ 梯度衰减因子包括激活函数导数，此外，还有多个权重连乘也会影响。。。梯度消失只是表面说法，按照这样理解，底层使用非常大的学习率，或者人工添加梯度噪音，原则上也能回避，有不少论文这样试了，然而目前来看，有用，但没太大的用处。深层原因训练不好的本质难题可能不是衰减或者消失（残差网络论文也提到这一点），是啥目前数理派也搞不清楚，所以写了论文也顺势这样说开了。不然，贸贸然将开山鼻祖的观点否定了，是需要极大勇气和大量的实验，以及中二精神的。
1. Sigmoid
sigmoid函数也称为Logistic函数，因为Sigmoid函数可以从Logistic回归（LR）中推理得到，也是LR模型指定的激活函数。
sigmod函数的取值范围在（0, 1）之间，可以将网络的输出映射在这一范围，方便分析。
Sigmoid公式及导数：
Sigmoid及其导数曲线：
Sigmoid作为激活函数的特点：
优点：平滑、易于求导。
缺点：
- 激活函数计算量大（在正向传播和反向传播中都包含幂运算和除法）；
- 反向传播求误差梯度时，求导涉及除法；
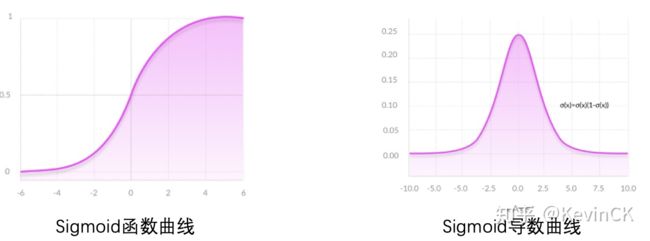
- Sigmoid导数取值范围是[0, 0.25]，由于神经网络反向传播时的“链式反应”，很容易就会出现梯度消失的情况。例如对于一个10层的网络， 根据 0.25^10 ≈ 0.000000954，第10层的误差相对第一层卷积的参数 W1 的梯度将是一个非常小的值，这就是所谓的“梯度消失”。
- Sigmoid的输出不是0均值（即zero-centered）；这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入，随着网络的加深，会改变数据的原始分布。
2. tanh
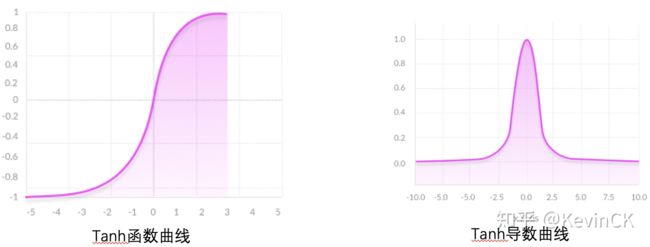
tanh为双曲正切函数，其英文读作Hyperbolic Tangent。tanh和 sigmoid 相似，都属于饱和激活函数，区别在于输出值范围由 (0,1) 变为了 (-1,1)，可以把 tanh 函数看做是 sigmoid 向下平移和拉伸后的结果。
tanh公式：
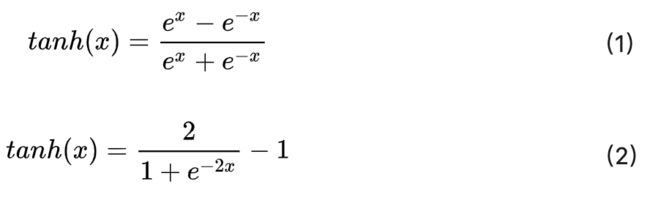
从公式2中，可以更加清晰看出tanh与sigmoid函数的关系（平移+拉伸）。
tanh及其导数曲线：
tanh作为激活函数的特点：
相比Sigmoid函数，
- tanh的输出范围时(-1, 1)，解决了Sigmoid函数的不是zero-centered输出问题；
- 幂运算的问题仍然存在；
- tanh导数范围在(0, 1)之间，相比sigmoid的(0, 0.25)，梯度消失（gradient vanishing）问题会得到缓解，但仍然还会存在。
3. ReLU
Relu(Rectified Linear Unit)——修正线性单元函数：该函数形式比较简单，
公式：relu=max(0, x)
ReLU及其导数曲线：
从上图可知，ReLU的有效导数是常数1，解决了深层网络中出现的梯度消失问题，也就使得深层网络可训练。同时ReLU又是非线性函数，所谓非线性，就是一阶导数不为常数；对ReLU求导，在输入值分别为正和为负的情况下，导数是不同的，即ReLU的导数不是常数，所以ReLU是非线性的（只是不同于Sigmoid和tanh，relu的非线性不是光滑的）。
ReLU在x>0下，导数为常数1的特点：
导数为常数1的好处就是在“链式反应”中不会出现梯度消失，但梯度下降的强度就完全取决于权值的乘积，这样就可能会出现梯度爆炸问题。解决这类问题：一是控制权值，让它们在（0，1）范围内；二是做梯度裁剪，控制梯度下降强度，如ReLU(x)=min(6, max(0,x))
ReLU在x<0下，输出置为0的特点：
描述该特征前，需要明确深度学习的目标：深度学习是根据大批量样本数据，从错综复杂的数据关系中，找到关键信息（关键特征）。换句话说，就是把密集矩阵转化为稀疏矩阵，保留数据的关键信息，去除噪音，这样的模型就有了鲁棒性。ReLU将x<0的输出置为0，就是一个去噪音，稀疏矩阵的过程。而且在训练过程中，这种稀疏性是动态调节的，网络会自动调整稀疏比例，保证矩阵有最优的有效特征。
但是ReLU 强制将x<0部分的输出置为0（置为0就是屏蔽该特征），可能会导致模型无法学习到有效特征，所以如果学习率设置的太大，就可能会导致网络的大部分神经元处于‘dead’状态，所以使用ReLU的网络，学习率不能设置太大。
ReLU作为激活函数的特点：
- 相比Sigmoid和tanh，ReLU摒弃了复杂的计算，提高了运算速度。
- 解决了梯度消失问题，收敛速度快于Sigmoid和tanh函数，但要防范ReLU的梯度爆炸
- 容易得到更好的模型，但也要防止训练中出现模型‘Dead’情况。
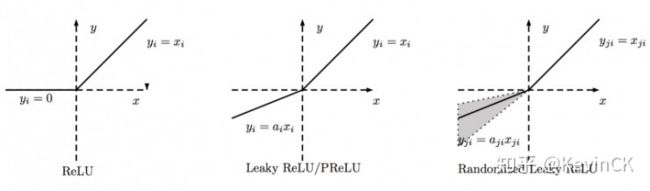
4. LeakyReLU, PReLU（Parametric Relu）, RReLU
为了防止模型的‘Dead’情况，后人将x<0部分并没有直接置为0，而是给了一个很小的负数梯度值 α。
Leaky ReLU中的 α 为常数，一般设置 0.01。这个函数通常比 Relu 激活函数效果要好，但是效果不是很稳定，所以在实际中 Leaky ReLu 使用的并不多。
PRelu（参数化修正线性单元） 中的 α 作为一个可学习的参数，会在训练的过程中进行更新。
RReLU（随机纠正线性单元） 也是Leaky ReLU的一个变体。在RReLU中，负值的斜率在训练中是随机的，在之后的测试中就变成了固定的了。RReLU的亮点在于，在训练环节中，aji是从一个均匀的分布U(I,u)中随机抽取的数值。
ReLU及其变体图像：
5. GELU
我们经常希望神经网络具有确定性决策，这种想法催生了 GELU 激活函数的诞生。这种函数的非线性希望对输入 x 上的随机正则化项做一个转换，听着比较费劲，具体来说可以表示为：Φ(x) × Ix + (1 − Φ(x)) × 0x = xΦ(x)。
我们可以理解为，对于一部分Φ(x)，它直接乘以输入 x，而对于另一部分 (1 − Φ(x))，它们需要归零。不太严格地说，上面这个表达式可以按当前输入 x 比其它输入大多少来缩放 x。
因为高斯概率分布函数通常根据损失函数计算，因此研究者定义高斯误差线性单元（GELU）为：
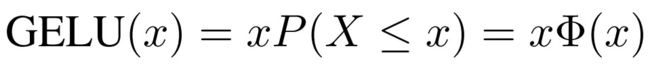
上面这个函数是无法直接计算的，因此可以通过另外的方法来逼近这样的激活函数，研究者得出来的表达式为：
# GPT-2 的 GELU 实现
def gelu(x):
return 0.5*x*(1+tf.tanh(np.sqrt(2/np.pi)*(x+0.044715*tf.pow(x, 3))))
5. softmax
softmax用于多分类过程中，它将多个神经元的输出，映射到（0,1）区间内，可以看成概率来理解，从而来进行多分类！
假设我们有一个数组，V，Vi表示V中的第i个元素，那么这个元素的softmax值就是:
更形象的如下图表示：
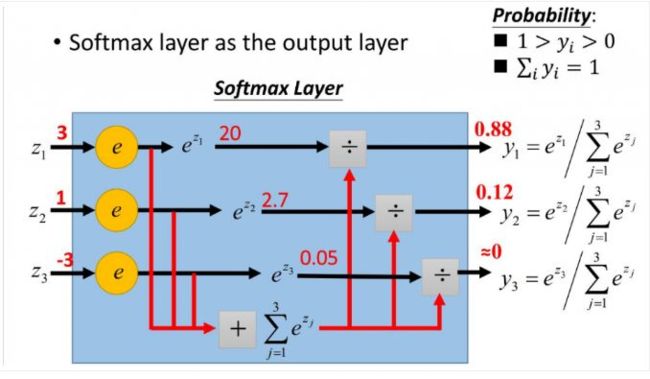
softmax直白来说就是将原来输出是3,1,-3通过softmax函数一作用，就映射成为(0,1)的值，而这些值的累和为1（满足概率的性质），那么我们就可以将它理解成概率，在最后选取输出结点的时候，我们就可以选取概率最大（也就是值对应最大的）结点，作为我们的预测目标！