ORBSLAM2学习（二）：ORB源码分析

1.前言

       有关ORB算法的原理部分详细介绍，见链接。ORBSLAM2中使用到了opencv，而opencv中已经带有了ORB的实现，且考虑了旋转不变性和尺度不变性，那为何作者还要自己实现ORB呢。一个原因是opencv中ORB特征提取后一般会出现特征点分布不均的情况，作者自己实现的ORB则使用一些方法使特征点分布地更加均匀（应该是对后面特征点匹配有好处吧）。

2.代码文件

       ORB算子的相关文件是ORBExtractor.cc和ORBExtractor.h，作者定义了ORBextractor算法类。其中需要在初始化时显式赋值的成员变量有nfeatures（指定要提取得到的关键点数量）、scaleFactor（金字塔图像缩放因子，这里大于1）、nlevels（金字塔图像层数，如果为1则不存在缩放）、iniThFAST(FAST检测角点时的初始化阈值)、minThFAST(FAST检测角点的最低阈值，在使用iniThFAST检测不到角点时使用该值)。

3.代码分析

3.1构造函数

      调用ORB算法流程很简单，首先调用构造函数ORBextractor(int nfeatures, float scaleFactor, int nlevels,int iniThFAST, int minThFAST)构造算法对象。下面对构造函数做了一些必要的注释

ORBextractor::ORBextractor(int _nfeatures, float _scaleFactor, int _nlevels,
         int _iniThFAST, int _minThFAST):
    nfeatures(_nfeatures), scaleFactor(_scaleFactor), nlevels(_nlevels),
    iniThFAST(_iniThFAST), minThFAST(_minThFAST)
{
    mvScaleFactor.resize(nlevels);
    mvLevelSigma2.resize(nlevels);
    mvScaleFactor[0]=1.0f;
    mvLevelSigma2[0]=1.0f;
    for(int i=1; i= vmin; --v)
    {
        while (umax[v0] == umax[v0 + 1])
            ++v0;
        umax[v] = v0;
        ++v0;
    }// 这部分是计算一个圆形中y坐标对应的x坐标范围，作者使用一些方法保证取值是对称的
}
ORB an efficient alternative to SIFT or SURF》中计算得到的匹配对的x/y坐标，一共256对
    std::copy(pattern0, pattern0 + npoints, std::back_inserter(pattern));

    //This is for orientation
    // pre-compute the end of a row in a circular patch
    umax.resize(HALF_PATCH_SIZE + 1);

    int v, v0, vmax = cvFloor(HALF_PATCH_SIZE * sqrt(2.f) / 2 + 1);
    int vmin = cvCeil(HALF_PATCH_SIZE * sqrt(2.f) / 2);
    const double hp2 = HALF_PATCH_SIZE*HALF_PATCH_SIZE;
    for (v = 0; v <= vmax; ++v)
        umax[v] = cvRound(sqrt(hp2 - v * v));

    // Make sure we are symmetric
    for (v = HALF_PATCH_SIZE, v0 = 0; v >= vmin; --v)
    {
        while (umax[v0] == umax[v0 + 1])
            ++v0;
        umax[v] = v0;
        ++v0;
    }// 这部分是计算一个圆形中y坐标对应的x坐标范围，作者使用一些方法保证取值是对称的
}

3.2.提取关键点并计算描述子

       之后调用成员函数（重载的()操作符）即可得到ORB关键点和特征描述子。由于相关代码全部展开篇幅过大，这里我只把调用的函数分步骤做了注释，并在后面着重在原理上逐步做了注解。

void ORBextractor::operator()( InputArray _image, InputArray _mask, vector& _keypoints,
                      OutputArray _descriptors)
{ 
    if(_image.empty())
        return;

    Mat image = _image.getMat();
    assert(image.type() == CV_8UC1 );// 只处理灰度图

    // Pre-compute the scale pyramid
    ComputePyramid(image);// step1：构造金字塔图像

    vector < vector > allKeypoints;
    ComputeKeyPointsOctTree(allKeypoints);// Step2：计算关键点
    //ComputeKeyPointsOld(allKeypoints);

    Mat descriptors;

    int nkeypoints = 0;
    for (int level = 0; level < nlevels; ++level)
        nkeypoints += (int)allKeypoints[level].size();
    if( nkeypoints == 0 )
        _descriptors.release();
    else
    {
        _descriptors.create(nkeypoints, 32, CV_8U);
        descriptors = _descriptors.getMat();
    }

    _keypoints.clear();
    _keypoints.reserve(nkeypoints);

    int offset = 0;
    for (int level = 0; level < nlevels; ++level)
    {
        vector& keypoints = allKeypoints[level];
        int nkeypointsLevel = (int)keypoints.size();

        if(nkeypointsLevel==0)
            continue;

        // preprocess the resized image
        Mat workingMat = mvImagePyramid[level].clone();
        GaussianBlur(workingMat, workingMat, Size(7, 7), 2, 2, BORDER_REFLECT_101);// Step3：计算关键点方向

        // Compute the descriptors
        Mat desc = descriptors.rowRange(offset, offset + nkeypointsLevel);
        computeDescriptors(workingMat, keypoints, desc, pattern);// Step4：计算关键点描述子

        offset += nkeypointsLevel;

        // Scale keypoint coordinates
        if (level != 0)
        {
            float scale = mvScaleFactor[level]; //getScale(level, firstLevel, scaleFactor);
            for (vector::iterator keypoint = keypoints.begin(),
                 keypointEnd = keypoints.end(); keypoint != keypointEnd; ++keypoint)
                keypoint->pt *= scale;// 根据金字塔图像缩放比例恢复关键点在原始图像中的位置
        }
        // And add the keypoints to the output
        _keypoints.insert(_keypoints.end(), keypoints.begin(), keypoints.end());// Step5：保存关键点
    }
}

       该部分算法具体流程如下：

Step1.根据scaleFactor和nlevels计算金字塔图像

       代码中为每层金字塔图像构造了一个边界上做了扩展的副本，通过copyMakeBorder()实现，为了对处于边界处的像素做操作。

Step2.计算关键点，使用ComputeKeyPointsOctTree()函数。对于每一层金字塔图像

1）将图像按照30X30像素大小划分为网格，每个网格内使用FAST提取关键点(cv::FAST()函数)

        当使用iniThFAST提取不到角点时，会使用minThFAST重新提取一次

2）实际提取的关键点数一般超过目标数量，需要做取舍，作者在该过程中使用一些方法使得选取的特征点评分较高（质量较好）且分布尽量均匀（DistributeOctTree()函数）。具体操作为首先构造一种改进的4叉树来表示实际提取的关键点，4叉树中每个节点拥有自己占有的物理空间和在内的关键点。之后将会根据物理空间等大小做“1分4”的分裂，一个父节点分裂为4个子节点，同时把原有的关键点根据位于那个子节点内部划分给该子节点。当满足一定条件时（4叉树叶子节点数量大于等于目标关键点数量时或者叶子节点数量不再变化时）4叉树不再分裂。此时4叉树中每个叶子节点的实际物理位置在图像中是比较均匀的。当4叉树叶子节点具有的关键点数目大于1时，选取其中评分最高的一个作为代表性关键点。此时就完成了关键点的选取工作。

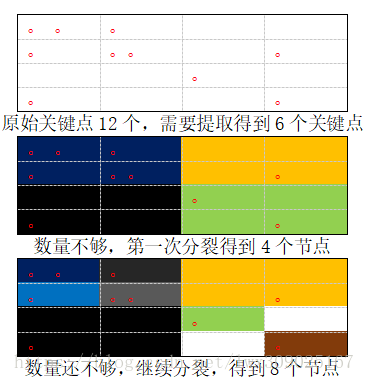
       有关对关键点使用4叉树做类似于聚集操作的过程，可参考下图。下图中红色圆点代表关键点，由于目标关键点数小于原始关键点数，我们通过对原始空间做均匀大小地4等划分，在空间内节点数量不大于1时不对该空间继续划分。图中划分至第二次时，存在了8个空间节点，已经超过了目标数量。此时代码中把当前节点按照包含的关键点数量降序排列，选取前6个作为目标关键点所在的空间节点。同时存在一些空间节点具有大于1个的关键点，我们可以根据这些关键点的评分（规则可自己定义，作者选取的是 opencv中KeyPoint类的response成员变量表征其质量高低）选取最优的那个作为该节点的代表关键点。

 

Step3.使用强度质心法计算每个关键点的方向

        这点没什么可说的，调用的是IC_Angle()函数

Step4.对金字塔图像做高斯滤波；使用BRIEF计算各个关键点的描述子，其中会用到Step3中求得的方向对匹配点对做旋转操作以实现旋转不变性

        调用GaussianBlur()做高斯滤波；

      调用computeOrbDescriptor()计算关键点的描述子；std::vector pattern保存的是根据论文《ORB an efficient alternative to SIFT or SURF》中启发式搜索算法计算得到的256对匹配对坐标。为了保证图像旋转情况下描述子计算结果的不变性（旋转不变性），会把匹配对坐标按照Step3中得到的角度做旋转，然后根据旋转结果在图像中得到其灰度值做比较

Step5.保存所有的关键点和对应的描述子

4.算法结果

 

       作者使用一些方法让ORB提取的关键点分布尽量均匀，这是和opencv自带的ORB描述子最为不同的一点，有人做了比较。下图中左边是ORBSLAM2中提取的关键点表示，右图是opencv中ORB算子提取的关键点表示，可以看出左边图像中关键点的分布明显更加均匀。