通过 Python 代码实现时间序列数据的统计学预测模型
通过 Python 代码实现时间序列数据的统计学预测模型
在本篇中,我们将展式使用 Python 统计学模型进行时间序列数据分析。
*** 问题描述 ***
目标:根据两年以上的每日广告支出历史数据,提前预测两个月的广告支出金额。
原始数据:2017-01-01 到 2019-09-23 期间的每日广告支出。
数据准备:划分训练集和测试集。
df1 = data[['Date','Spend']].set_index('Date')
train = df1.iloc[:933,:]
test = df1.iloc[933:,:]
test.shape,train.shape
测试集大小:(63,1);训练集大小:(933,1)。
本文目录
- 综述
- 时间序列分析常用统计模型
- 单变量时间序列数据建模的关键要素
- ARIMA
- ACF 和 PACF
- SARIMA
- 案例:通过 SARIMA 预测广告支出
- ETS
- ETS
- Holt-Winter 季节性预测算法
- 案例:通过 Holt-Winter 季节性预测算法预测广告支出
- 算法对比
- 结束语
综述
时间序列分析常用统计模型
- 单变量时间序列统计学模型,如:平均方法、平滑方法、有/无季节性条件的 ARIMA 模型。
- 多变量时间序列统计学模型,如:外生回归变量、VAR。
- 附加或组件模型,如:Facebook Prophet、ETS。
- 结构化时间序列模型,如:贝叶斯结构化时间序列模型、分层时间序列模型。
在本篇文章中,我们主要关注 SARIMA 和 Holt-winters 方法。
单变量时间序列统计学模型的关键要素
如果我们想要对时间序列数据进行上述统计学模型分析,需要进行一系列处理使得:(1)数据均值 (2)数据方差 (3)数据自协方差 这三个指标不依赖于时间项。即时间序列数据具有平稳性。
如何明确时间序列数据是否具有平稳性?可以从两个特征进行判断。(1) 趋势,即均值随时间变化;(2) 季节性,即方差随时间变化、自协方差随时间变化。若满足以上两个条件,则时间序列数据不符合平稳性要求。
可以通过以下方法消除上述问题:
- 变换,如:取对数、取平方等。
- 平滑处理,如:移动平均等。
- 差分。
- 分解。
- 多项式拟合,如:拟合回归。
ARIMA
Autoregressive Integrated Moving Average model (ARIMA),差分整合移动平均自回归模型。ARIMA(p,d,q)主要包含三项:
p:AR项,即自回归项(autoregression),将时间序列下一阶段描述为前一阶段数据的线性映射。
d项,即积分项(integration),时间序列的差分预处理步骤,使其满足平稳性要求
q:MA项,即移动平均项(moving average),将时间序列下一阶段描述为前一阶段数据平均过程中的残留误差的线性映射。
该模型需要指定 p d q 三项参数,并按照顺序执行。ARIMA 模型也可以用于开发 AR, MA 和 ARMA 模型。
ACF 和 PACF 图
自相关函数,autocorrelation function(ACF),描述了时间序列数据与其之后版本的相关性(如:Y(t) 与 Y(t-1) 之间的相关性)。
偏自相关函数,partial autocorrelation function(PACF),描述了各个序列的相关性。
- 通过 PACF 图可以确定 p
- 通过 ACF 图可以确定 q
SARIMA
季节性差分自回归滑动平均模型,seasonal autoregressive integrated moving averaging(SARIMA),在 ARIMA 模型的基础上进行了季节性调节。
其形式为:SARIMA(p,d,q)(P,D,Q)s,其中P,D,Q为季节参数,s为时间序列周期。
案例:通过 SARIMA 预测广告支出
首先,我们建立 test_stationarity 来检查时间序列数据的平稳性。
from statsmodels.tsa.stattools import adfuller
df1=df.resample('D', how=np.mean)
def test_stationarity(timeseries):
rolmean = timeseries.rolling(window=30).mean()
rolstd = timeseries.rolling(window=30).std()
plt.figure(figsize=(14,5))
sns.despine(left=True)
orig = plt.plot(timeseries, color='blue',label='Original')
mean = plt.plot(rolmean, color='red', label='Rolling Mean')
std = plt.plot(rolstd, color='black', label = 'Rolling Std')
plt.legend(loc='best'); plt.title('Rolling Mean & Standard Deviation')
plt.show()
print ('' )
dftest = adfuller(timeseries, autolag='AIC')
dfoutput = pd.Series(dftest[0:4],
index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
for key,value in dftest[4].items():
dfoutput['Critical Value (%s)'%key] = value
print(dfoutput)
test_stationarity(df1.Spend.dropna())
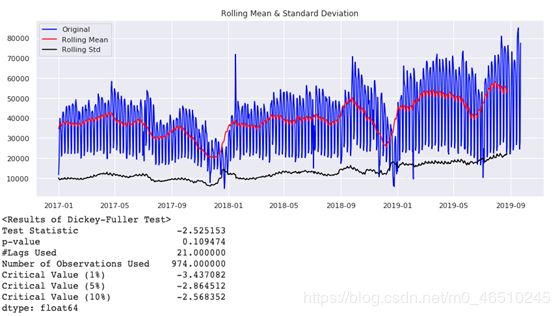
通过 test_stationarity 函数,可以绘制移动平均值以及标准差,并且通过 Augmented Dickey-Fuller test 输出 P 值。
对比临界值(critical value)可以看到,时间序列数据时非平稳的。
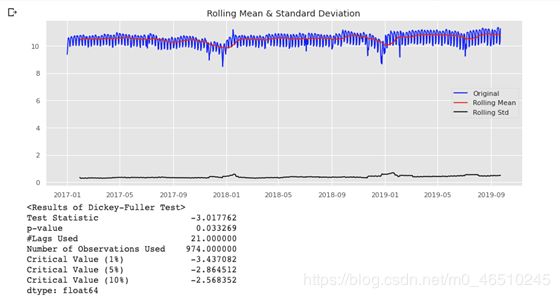
首先我们试试对数变换,能不能使数据达到平稳性要求。
可以看到,利用对数变换df1[‘log_Spend’]=np.log(df1[‘Spend’]),时间序列在阈值为5%时满足平稳性要求。
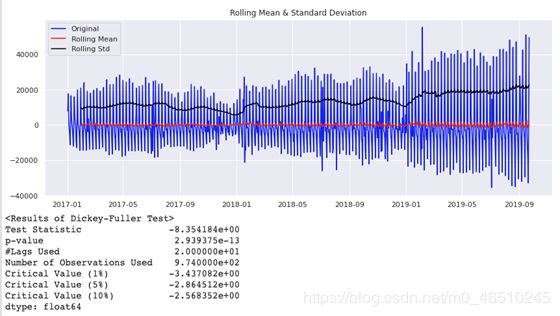
接下来,我们试试差分操作:test_stationarity(df1[‘Spend’].diff(1).dropna())。
显然,通过差分操作后,效果更好,时间序列在阈值为1%时满足平稳性要求。
然后,我们就可以建立 SARIMA 模型,并且预测 2019-07-23 到 2019-09-23 这两个月间每天的广告指出。
import statsmodels.api as sm
fit1 = sm.tsa.statespace.SARIMAX(train.Spend, order=(7, 1, 2), seasonal_order=(0, 1, 2, 7)).fit(use_boxcox=True)
test['SARIMA'] = fit1.predict(start="2019-07-23", end="2019-09-23", dynamic=True)
plt.figure(figsize=(16, 8))
plt.plot(train['Spend'], label='Train')
plt.plot(test['Spend'], label='Test')
plt.plot(test['SARIMA'], label='SARIMA')
plt.legend(loc='best')
plt.show()
现在,让我们通过从 sklearn.metrics 包导入 mean_squared_error,mean_absolute_error 函数计算 mse 和 mae 来检查这个模型的性能。结果如下:
![]()
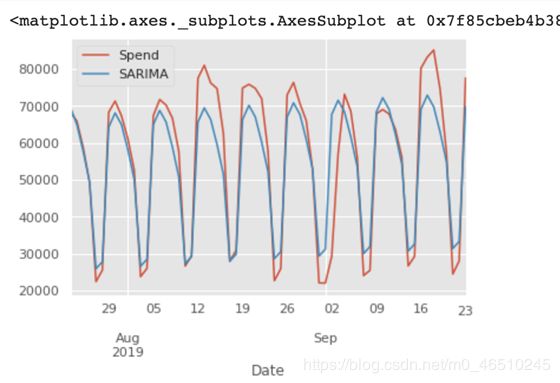
进行数据可视化:
从 mse、mae 以及预测曲线可以看出,SARIMA 模型成功预测了时间序列变化趋势和季节性特征。但是在峰值处的表现仍旧有待提高。
ETS
ETS,Exponential Smoothing
由于时间序列数据随时间变化但具有一定的随机性,我们通常希望对数据进行平滑处理。为此,我们将使用 ETS 技术,通过指数方法为过去的数据分配较少的权重。同时将时间序列数据分解为趋势(T)、季节(S)和误差(E)分量。
三种常用 ETS 方法如下:
- Linear:双指数平滑;
- Additive:三指数平滑;
- Multiplicative:三指数平滑。
Holt-Winter 季节性预测算法
Holt-winter 季节性预测算法是一种三指数平滑方法。它包含三个主要部分:水平、趋势、季节性分量。
案例:通过 Holt-Winter 季节性预测算法预测广告支出
通过 Holt-winter 季节性预测算法预测 2019-07-23 到 2019-09-23 期间的每日广告支出,代码如下:
from statsmodels.tsa.api import ExponentialSmoothing
fit1 = ExponentialSmoothing(np.asarray(train['Spend']) ,seasonal_periods=7 ,trend='add', seasonal='add').fit(use_boxcox=True)
test['Holt_Winter'] = fit1.forecast(len(test))
plt.figure(figsize=(16,8))
plt.plot( train['Spend'], label='Train')
plt.plot(test['Spend'], label='Test')
plt.plot(test['Holt_Winter'], label='Holt_Winter')
plt.legend(loc='best')
plt.show()
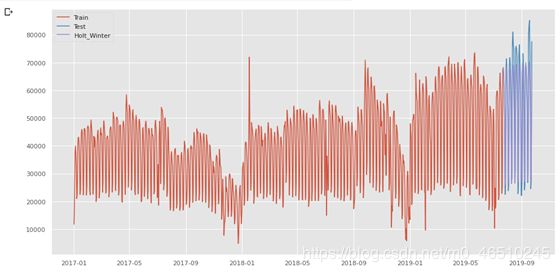
同样,我们通过 mean_squared_error,mean_absolute_error 函数查看 mse 和 mae。
![]()
可以看到,H-W 模型同样能够预测时间序列变化趋势和季节性特征。
算法对比
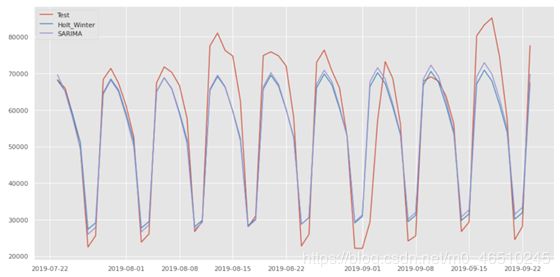
通过将两种算法的预测结果进行对比,可以评价哪种方法预测能力更好。
从图中可以看出,在MSE和MAE均较低的情况下,SARIMA模型的性能略优于Holt-Winter模型。尽管这两种模式都无法完美地抓住峰谷特征,但它们仍然对企业有用。根据数据,平均每月广告支出为2百万美元以上。而这两种算法的MAE大约在6000左右。换言之,对于一家平均每月广告支出为2百万美元的企业,两个月的广告支出预测误差只在6000美元左右,这是相当可观的。
结束语
在本文中,单变量预测方法在广告支出数据上表现良好。但这些方法难以组合/合并新的信号(如事件、天气)。同时这些方法对丢失数据也非常敏感,通常不能很好地预测很长一段时间。