一本正经的聊数据结构(7):哈弗曼编码
前文传送门:
「一本正经的聊数据结构(1):时间复杂度」
「一本正经的聊数据结构(2):数组与向量」
「一本正经的聊数据结构(3):栈和队列」
「一本正经的聊数据结构(4):树」
「一本正经的聊数据结构(5):二叉树的存储结构与遍历」
「一本正经的聊数据结构(6):最优二叉树 —— 哈夫曼树」
引言
在上一期,我们介绍了什么是哈夫曼树以及哈夫曼树的构建过程,本期我们接着介绍哈夫曼树的用途。
字符编码压缩
哈夫曼树的应用很广,哈夫曼编码就是其在电讯通信中的应用之一。广泛地用于数据文件压缩的十分有效的编码方法,其压缩率通常在 20% ~ 90% 之间。
在电讯通信业务中,通常用二进制编码来表示字母或其他字符,并用这样的编码来表示字符序列。
在计算机当中,因为计算机不是人,不能识别图像、声音、视频等内容,对于计算机来讲,它只能认识二进制的 0 和 1 ,在数字电子电路中,逻辑门的实现直接应用了二进制,因此现代的计算机和依赖计算机的设备里都用到二进制。
我们在计算机上看到的一切的图像、声音、视频等内容,都是由二进制的方式进行存储的。
简单来讲,我们把信息转化为二进制的过程可以称之为编码,在计算机的世界里,编码有很多种格式,比如我们常见的: ASCII 、 Unicode 、 GBK 、 GB2312 、 GB18030 、 UTF-8 、 UTF-16 等等。
编码方式从长度上来分大致可以分为两个大类:
- 定长编码:定长仅表明段与段之间长度相同,但没说明是多长。
- 变长编码:变长就是段与段之间的长度不相同,同样也不定义具体有多长。
在最初的设计中, ASCII 编码就是采用的定长编码的方案,使用定长一字节来表示一个字符。
举个栗子,假如我们对 「hello」 进行编码,使用定长编码,为了方便,采用了十进制,主要是因为我懒,原理与二进制是一样的。
| 字符 | 编码 |
|---|---|
| h | 00 |
| e | 01 |
| l | 02 |
| o | 03 |
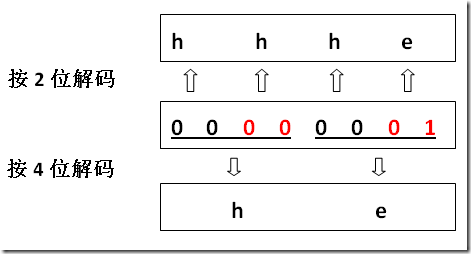
假设我们现在有个文件,内容是 00000001 ,假如定长 2 位(这里的位指十进制的位)是唯一的编码方案,用它去解码,就会得到 「hhhe」 (可以对比上面的编码, 00 代表 h ,所以前 6 个 0 转化成 3 个 h ,后面的 01 则转化成 e )。
但是,如果定长 2 位不是唯一的编码方案呢?如上图中的定长 4 位方案,如果我们误用定长 4 位去解码,结果就只能得到「he」( 0000 转化为 h , 0001 转化为 e )
随着时代的发展,不仅老美要对他们的英文进行编码,我们中国人也要对汉字进行编码,而早期的 ASCII 码的方案只有一个字节,对我们汉字而言是远远不够的,所以在我们的汉字编码方案 GB2312 中,汉字是使用两个字节来表示的(这也是迫不得已的事,一字节压根不够用) 。
再多说一句,实际上我们的 GB2312 是一种变长的编码方案,主要是为了兼容一个字节的 ASCII 码。
随着计算机在全世界的推广,各种编码方案都出来了,彼此之间的转换也带来了诸多的问题。采用某种统一的标准就势在必行了,于是乎天上一声霹雳, Unicode 粉墨登场!
不过 Unicode 对于只需要使用到一个字节的 ASCII 码来讲,让他们使用 Unicode ,多少还是不是很愿意的。
比如 「he」 两个字符,用 ASCII 只需要保存成 6865 ( 16 进制),现在则成了 00680065 ,前面多的那两个 0 (用作站位) ,基本上可以说是毫无意义,用 Unicode 编码的文本,原来可能只有 1KB 大小,现在要变成 2KB ,体积成倍的往上涨。
最终, Unicode 编码方案逐渐演化成了变长的 UTF-8 编码方案,并且 UTF-8 是可以和 ASCII 码进行兼容。
UTF-8 因为能兼容 ASCII 而受到广泛欢迎,但在保存中文方面,要用 3 个字节,有的甚至要 4 个字节,所以在保存中文方面效率并不算太好,与此相对, GB2312 , GBK 之类用两字节保存中文字符效率上会高,同时它们也都兼容 ASCII ,所以在中英混合的情况下还是比 UTF-8 要好,但在国际化方面及可扩展空间上则不如 UTF-8 了。
所以如果有进军国际的想法,那么最好还是使用 UTF-8 编码。
哈弗曼编码
哈弗曼编码是一种不定长的编码方式,是由麻省理工学院的哈夫曼博所发明,这种编码方式实现了两个重要目标:
-
任何一个字符编码,都不是其他字符编码的前缀。
-
信息编码的总长度最小。
干巴巴的,还是接着举例子:
如果我们对 「ABACCDA」 进行编码,假设 A, B, C, D 的编码分别为 00, 01,10, 11。
那么 「ABACCDA」 编码后的结果是 「00010010101100」 (共 14 位),我们解码的时候只需要每两位进行拆分,就可以恢复编码前的信息了。
那我们如果用哈弗曼编码的方式进行编码呢?
第一件事情是要确定每个字母的权值(出现频率), 「ABACCDA」 这个字符串中 A, B, C, D 的权值(出现的频率)分别为 0.43, 0.14, 0.29, 0.14 。
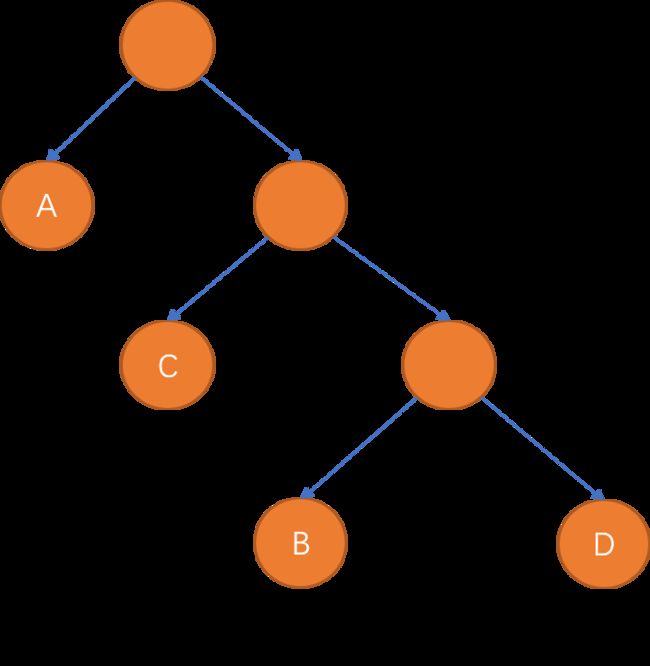
有了权值,我们可以构造一个哈弗曼树了,感兴趣的同学可以自己画一下,下面这个是我画的:
编码的结果就显而易见了: A:0, C:10, B:110, D:111 。
刚才那个 「ABACCDA」 编码后的结果就是 「0110010101110」 (共 13 位)。
上面我们知道了哈夫曼编码如何编码,那么我们拿到了一个经过哈弗曼编码后的代码,如何进行译码工作呢?
首先还是要知道每个字母的权重是多少,然后画出来这个哈弗曼树,接下来,就可以对照着这个哈弗曼树进行译码工作了。
在译码的过程中,若编码是 「0」 ,则向左走。若编码是 「1」 ,则向右走,一旦到达叶子结点,则译出一个字符。然后不停的重复,直到这个编码的结束,就是我们需要的原内容了。
参考
https://www.cnblogs.com/wkfvawl/p/9783271.html
https://my.oschina.net/goldenshaw/blog/307708