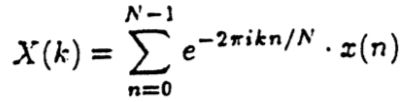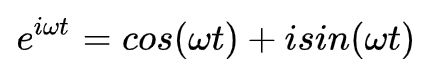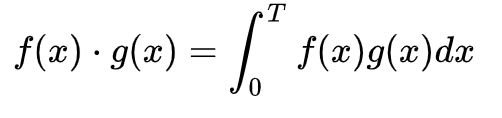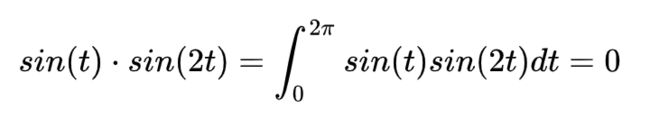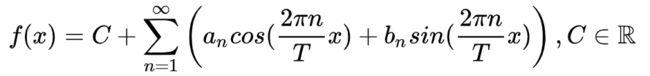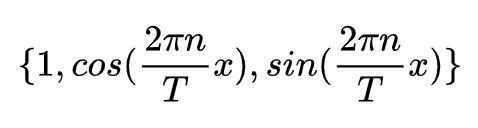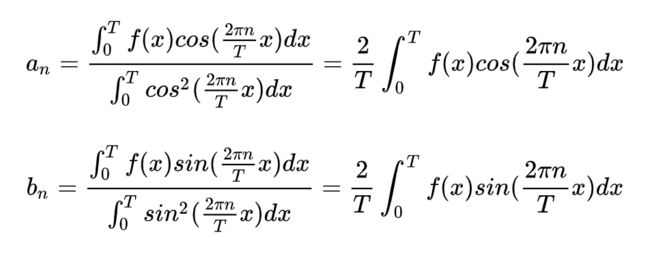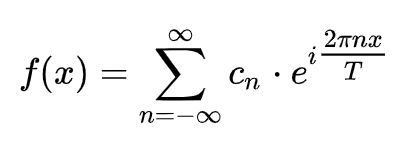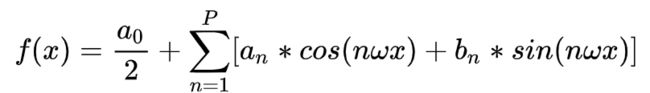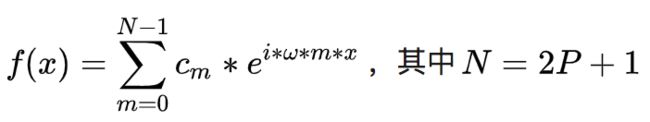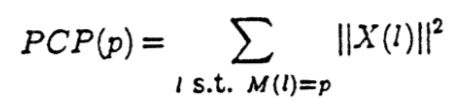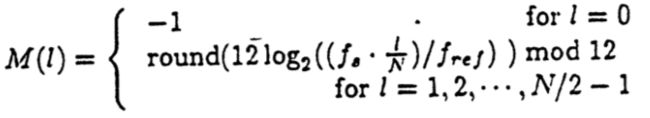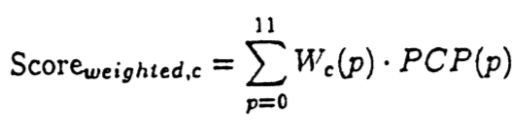论文解读一——PCP

《Real-Time Chord Recognition of Musical Sound: A System Using Common Lisp Music》

此篇论文中在早年，描述了一种实时地从音乐的声音信号中识别出和弦的方式。它的主要思路，是将连续的声信号输入，转换成音乐中的十二平均律，对应到钢琴中一个八度的键当中，识别出和弦的每一个音。

核心算法与基本思路：

首先我们将输入的声音信号获取进来，转换成一个离散傅立叶变换(DFT)的一个声谱图，之后我们将这个声谱图转换成一个音级轮廓图PCP(Pitch Class Profile)。然后再根据准备好的和弦模版与PCP进行模式匹配，最终得到根音以及最后的和弦类型。

一、DFT

关于傅立叶变换

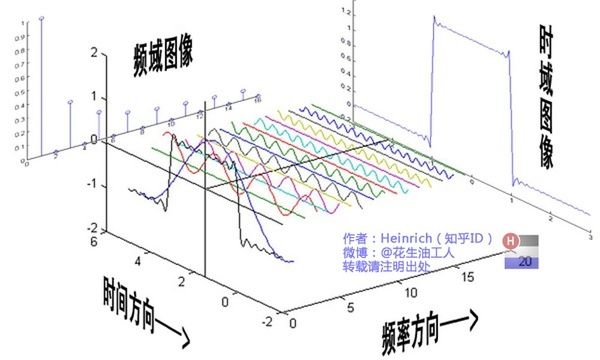
傅里叶变换的主要作用是将基于时间-能量的时域图转化为基于频率-能量的频域图。它的本质原理是将不规则的曲线分解为若干不同频率正弦波的线性和。

下面这张图能够很直观的表达这种变换关系

频域与时域

傅立叶变换根据下图来划分变换类型

变换方式

首先，此算法将输入声音信号流转换为一个DFT图，假设f_s为采样频率，x(n)为N个采样点中的第n个输入声信号片段。那么DFT谱图的公式如下，其中k = 0,1,2...N-1，而我们的X(0)，X(1)...X(N/2 - 1)表达了我们的整个频谱。

DFT变换公式

看到这个公式我们肯定会思考几个问题：
1、X(k)表达了什么？为什么X向量的个数与采样点数相关？
2、公式里最难理解的e ^-2πikn/N表达了什么？根据之前的描述，不是应该将正弦函数作为基的吗？
3、如何将X(k)转换成上述我们直观看到的频域图？

第一个问题

X(k)表达了f_s * (k/N)频率波的正弦系数。我们的问题中关注到，它所能表达的频率与采样的点数是相关的。这从道理上来说是合理的，采样的点越丰富(越详细)，我们能描述越细致的频率。

第二个问题

我们在看到傅立叶变换原理时，会想到的方法可能是构造正余弦函数的线性和，并设计很多参数，最后通过一些手段将参数求出来。

其实这样的思路本质上是没有什么问题的，我们的目标也正是将函数拆解成若干正余弦函数的组合。有科学家发现，所有的周期函数，都可以使用sin和cos函数的加减组合而成。

那么下面的问题是，如果我们原函数的周期是T，那么如何保证组合出来的函数周期也为T呢？

假如sin(x)的周期是2π，那么sin(2x)的周期也为2π(虽然最小周期是π)。更一般的，如果f(x)的周期为T，那么下式的周期也为T。所以对这些函数的加减，可以保证组成的函数一定周期也为T。

周期为T的三角函数

接下来，对三角函数振幅进行一些调整，再对三角函数进行加加减减

三角函数逼近线性函数

最终我们构造的逼近和大概是这样的，这个式子表达的是，无穷多种频率的正余弦波线性的组合。

三角函数线性和

在这里C称为直流分量，它表达函数整体非周期性地偏移，a _n和b _n是线性系数。我们的目标就是求出这三类系数。

欧拉公式
e^xi = cosx + isinx
使用e为底的表达式去表达正弦和余弦函数的线性组合，这时另一种表达正余弦函数的方式（关于推导，将e^x、sinx和cosx按照泰勒展开可得）。
那么欧拉公式究竟表达了什么含义呢？
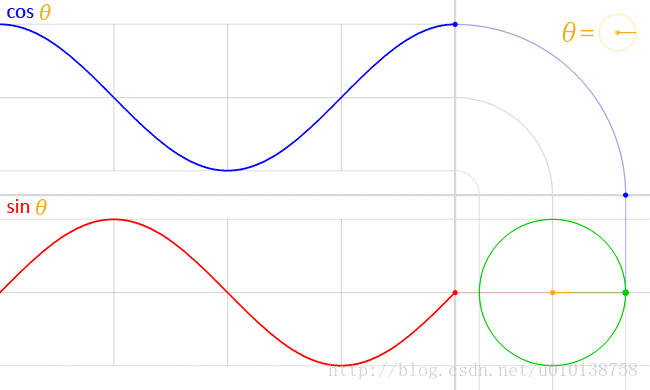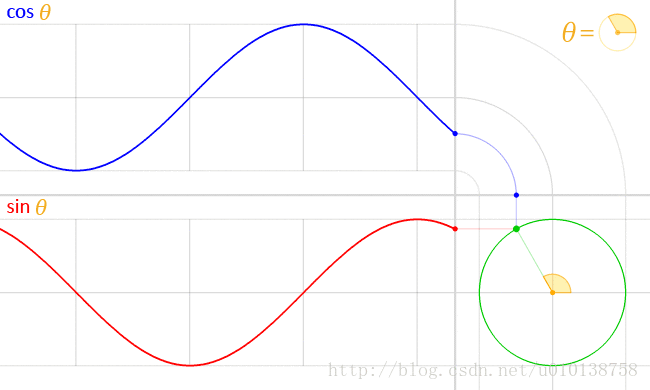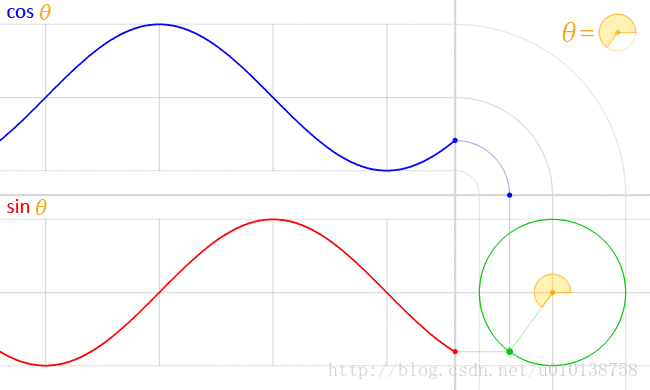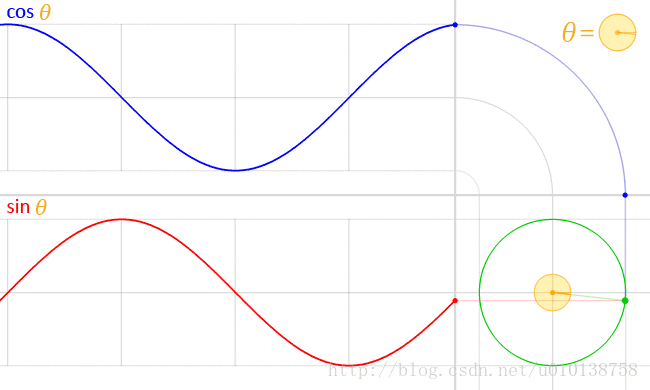
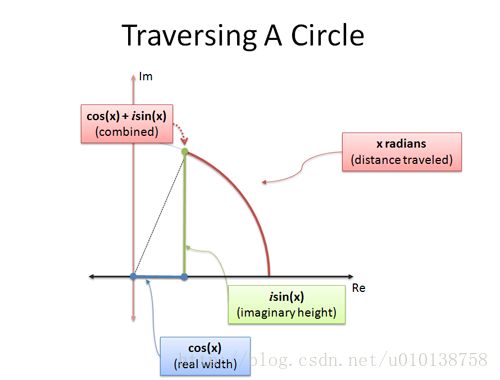
我们都知道，正弦和余弦函数实际上都是在描述一种圆周运动

正弦圆周运动

image.png

欧拉公式也是在描述一种特定的圆周运动，不过在复平面，我们使用向量来表示它，而欧拉公式的返回值是x时刻的点的位置（向量坐标），用复数来表示，不同于正弦函数(它返回的是x时刻的点的有坐标值)。从描述圆周运动的角度，它们是一致的，它们都是根据时间x返回圆周运动上的点的一个指标上的值。复数和实数都是数，更或者说是信息的一种编码形式。欧拉公式返回的复数的实部表示点在x轴的坐标值，虚部表示点在y轴上的坐标值。

复平面上的圆周运动

假设我们的函数可以进行以下分解

g(t) = sin(t) + sin(2t)

如果转到复平面去，那么它应该是这个欧拉公式所构造式子的虚部

g(t) = Im(e^it + e^i2t)

很显然，根据刚才的说法e^it + e^i2t所表达的是两个向量的和

向量组合

更一般地，我们可以写出函数向量的表达式

函数向量

并且函数向量的点积是这么定义的

image.png

根据函数点积的定义，我们可以自己计算得出下式

点积

这个式子说明了，sin(t)与sin(2t)是 正交的函数向量，它们线性无关，是正交基。如果写成g(t) = 1 * sin(t) + 1 * sin(2t)，表明可以理解为g(t)在正交基sin(t)和sin(2t)下的坐标是(1,1)。

那么如何求得对应函数向量的坐标呢？
假设w = au + bv（w、u、v都是向量，其中u和v是正交的）
那么基u的坐标a可以用以下公式求得：

基u的坐标

那么对于我们的此式子来说

sin(x)这个向量函数的坐标应该为

sin(x)基坐标

现在回顾以下我们之前的假设

正弦波的线性和

我们可以改写成这样（所有频率不同的正余弦向量函数在共同的周期内一定正交）

正交基下的假设函数

也就是说我们在求下列正交基的系数

正交基

于是我们可以得到系数

系数方程

由积分的周期性，更一般地，我们可以将上式泛化成

更一般地系数方程

好的！现在离我们的结果已经很接近了！我们将欧拉公式进行变换，如下图所示

欧拉变换

我们可以得到另一种形式的f(x)

傅立叶级数

其中

image.png

看到这里注意一个问题，这个式子连同上述的公式，描述的都是一个无穷序列上的傅立叶变换，但是在现实中，我们只能描述一个有限长的序列。 好在离散傅立叶变换在有限长序列上，它可以做到无限逼近，并且随着不同频率的正余弦波叠加数越多，它的精确度越高。

我们可以得到离散形式下的f(x)，它表达了P种不同频率的波叠加而成的函数，其中ω是所有频率波中的单位频率，它决定了波叠加的效果，ω=2π/N。

ω直观的含义，我们可以从正弦波的本质出发，我们都知道正弦波其实是在描述圆周运动，圆周运动的角速度为2π，那么这个波会以2π的速度绘制，那么它频率将会是2π。于是我们知道ω=2π/N描述的是角速度为ω的圆周运动。

离散傅立叶

使用欧拉变换后的f(x)

当 n=1,2,3...P 时，使

使用欧拉变换后的f(x)

由于单位频率为2π/N时，有一个这样的特殊条件：

对称特殊条件

因此，上述表达式可以写成下面这种整合后的形式

复数形式

此时，我们的C _n就等效于论文中的X(k)，用以下式子求出

复平面系数

不过可以注意到，论文中的公式没有1/N，其实有没有1/N都无所谓，并不影响它的相对大小，毕竟我们需要分析的是频谱之间相对差。

其中C_n在n=0时，表达的是直流分量，n=1...P的范围内（即1...(N-1)/2），可以表达所有的系数，n=P+1..N上的系数只是一个对称。
故而，一般情况下，我们需要求出前半部分的系数即可

现在再来回顾一下我们的公式，相信已经很容易理解了。
这里与论文中叙述一致，我们仅需要求出X(k)(k = 0 ... N / 2 - 1)的值即可。这里的X(k)与C_n表达的等价

image.png

实际上，C_n是对应频率的波在复平面内的点坐标，利用这个我们可以求出对应频率波的振幅。

第三个问题

DFT之后对应频谱的某点C_n或者X(k)可以用复数a+bi表示。那么这个复数的模就是Ak=√(a * a+b * b)，那么振幅A为

A = Ak/(N/2)。

对于n=0点的信号，它的振幅为0，通常作为一个整体偏移的作用存在，称为直流分量，幅度即为A1/N。

最后我们注意一点，由于DFT结果的对称性，通常我们只使用前半部分的结果，即小于采样频率一半的结果。（由奈奎斯特理论可得，可还原的信号量频率必小于采样频率的二分之一。）

二、PCP

对于X(k)，我们可以继续推导出PCP，它12维向量表示钢琴中八度里的12个半调音级。
设p = 0,1,2...11，那么我们定义式(1)PCP(p)如下：

image.png

在这里 M(l)映射着频谱与PCP，我们的 M(l)定义 式(2)如下：

image.png

其中f _ref表示以PCP(0)为基准的相对频率，f _s * (1/N)表示在DFT频谱内的。
这个算法有些难以理解，首先我们关注到f _ref的含义，
它表达着相对于这个PCP数组ps = [16.35, 17.32, 18.35, 19.45, 20.60, 21.83, 23.12, 24.50, 25.96, 27.50, 29.14, 30.87]中对应位置的值。
这里的算法描述再给出：
1、首先对于 式(2)使用p = 0, 1 ... 11，使得f _ref = ps[p]
2、令l = 1,2...N/2 - 1，将f _ref带入 M(l)，，计算出所有满足p = M(l)的l值
3、最后将对应p和所有l带入 式(1)中，求解出所有对应l频率的向量模长的平方。
此时，我们计算得到的PCP是一个12维的向量，每个向量代表这这个音级的强度。

三、模式识别

在论文里，选择了27组和弦，论文使用上述过程，进行手工调整得到了模版PCP。

image.png

论文中给出了两种方式对匹配性能进行评估：

• 临近法

  
  
  

  image.png
  
  

  此方法计算和弦模版的PCP与实际PCP的平方和，选取值最小的作为正确的和弦。

• 加权求和法

  
  
  

  image.png
  
  

  此方法计算和弦模版的权值与PCP的乘积之和，选取值最小的和弦作为正确的和弦。

四、启发式优化

1、进行pcp平滑化
2、和弦转变感知
3、PCP预处理
4、消除M(l)中无关紧要的区域
5、使用DFT窗口
6、静音检测
7、噪音检测

---

引用
https://blog.csdn.net/u010138758/article/details/73800339
https://www.zhihu.com/question/23234701/answer/26017000
https://blog.csdn.net/u010138758/article/details/73800339
https://dsp.stackexchange.com/questions/13722/pitch-class-profiling
https://stackoverflow.com/questions/36752485/python-code-for-pitch-class-profiling
http://blog.jobbole.com/70549/