图的深度遍历和广度遍历

理论部分

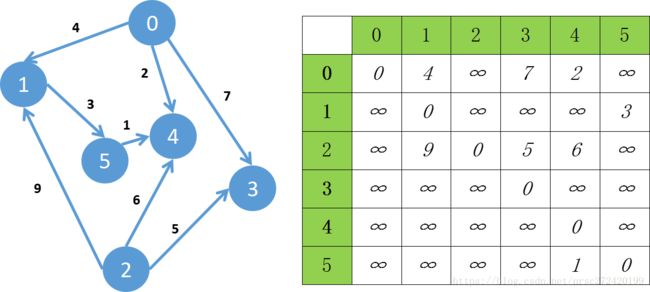
图的深度遍历和广度遍历都不算很难像极了二叉树的前序遍历和层序遍历,如下面的图,可以用右边的邻接矩阵进行表示,假设以顶点0开始对整幅图进行遍历的话,两种遍历方式的思想如下:

1. 深度优先遍历(depthFirstSearch—DFS)

由初始顶点开始,沿着一条道一直走,当走到走不动的时候,再回来走一条可以走的通的道,然后再继续往下走,直到走不动,再回来…对应于本图来说就是从0开始往前走,到1----->然后从1再往前走,到5----->从5再往前走,到4------->到了这里发现没路可走了------>就往回走,回到5,看5还有没有路,发现没路----->则回到1,看1有没有路,也没有----->再回到0,看0有没有路,发现有------>则由0走到3----->走到这里发现又没有路了----->再往回走,走到0,看0还有没有路,发现有----->则由0走到4,但是4已经被遍历过了,所以再回到0,结束这次遍历过程

但是这时候还有一个2没有遍历啊,该怎么办呢?之前我们是直接就默认从0开始进行往下遍历了,但是从0开始遍历没有一条路可以走到2,为了避免这种情况,我们必须得从每一个顶点开始遍历,这样才能避免漏掉这种只出不进的顶点

于是深度优先遍历得到的遍历结果应为:0 1 5 4 3 2

2.广度优先遍历(broadFirstSearch—BFS)

广度遍历我觉得理解起来更简单,就是一层一层的进行遍历,比如说以0顶点开始,0往下指向1,3,4,遍历的时候就先遍历0,然后再遍历它下一层的1,3,4------>然后分别遍历1,3,4的下一层---->而1,3,4只有1有下一层,则遍历1的下一层5,同理最后遍历2

即广度优先遍历得到的遍历结果应为:0 1 3 4 5 2

和二叉树的层序遍历一样,图的广度遍历也用到了队列,对于下图而言,先将0放入队首----->然后遍历0并将0从队列中取出,同时将0的邻接点1,3,4入队,这样队首就是1----->然后将1出队,并将1的邻接点入队(这里只有5), 这样队首就是3----->然后将3弹出并将3的邻接点入队(这里没有),这样队首就是4----->然后将4弹出并将4的邻接点入队(这里没有),队首就是从1入队的1的第一个邻接点(这里是5)---->然后将5弹出----->直到队列为空这样就完成了由定点0开始的广度优先遍历

我写的代码如下:

package cn.nrsc.graph;

import java.util.LinkedList;
import java.util.Queue;

//图的遍历
public class Graph {
	// ----------------------------图的表示方式------------------------
	private int vertexSize;// 顶点的数量
	private int[] vertexs;// 顶点对应的数组
	private int[][] matrix;// 邻接矩阵
	private static final int MAX_WEIGHT = 1000;// 代表顶点之间不连通
	private boolean[] isVisited; // 顶点是否已经被访问

	public Graph(int vertexSize) {
		this.vertexSize = vertexSize;
		this.matrix = new int[vertexSize][vertexSize];
		this.vertexs = new int[vertexSize];
		for (int i = 0; i < vertexSize; i++) {
			vertexs[i] = i;
		}

		isVisited = new boolean[vertexSize];
	}
	// ----------------------------图的表示方式------------------------

	// ----------------------------两个重要方法------------------------
	// 获取某个顶点的第一个邻接点
	public int getFirstNeighbor(int index) {
		for (int i = 0; i < vertexSize; i++) {
			if (matrix[index][i] > 0 && matrix[index][i] != 1000) {
				return i;
			}
		}
		return -1; // 如果没有第一个邻接点,则返回-1
	}

	// 获取某个节点V当前邻接点index的下一个邻接点
	public int getNextNeighbor(int v, int index) {
		for (int i = index + 1; i < vertexSize; i++) {
			if (matrix[v][i] > 0 && matrix[v][i] != 1000) {
				return i;
			}
		}
		return -1; // 如果没有返回-1
	}
	// ----------------------------两个重要方法------------------------

	// 图的深度优先遍历算法 ---- 从顶点i进行遍历
	private void depthFirstSearch(int i) {
		// 开始遍历顶点i---所以将其标记为已经遍历了
		isVisited[i] = true;
		// 遍历顶点i的第一个邻接点
		int FN = getFirstNeighbor(i);
		while (FN != -1) {// 如果第一个邻接点存在
			if (!isVisited[FN]) { // 且第一个邻接点没被遍历遍历过
				System.out.println("遍历到了" + FN + "顶点"); // 遍历该顶点
				// 同时递归遍历该顶点的邻接点
				depthFirstSearch(FN);
			}

			// 如果第一个邻接点已经遍历过了---则遍历其第一个邻接点后面的邻接点
			FN = getNextNeighbor(i, FN);
		}

	}

	// 对外提供的深度优先遍历
	public void depthFirstSearch() {
		// 假如图为有向图-----可能遍历到一定程度就再也走不通了
		// 如我例子中的节点2---所以需要对每一个节点进行一下循环
		for (int i = 0; i < vertexSize; i++)
			if (!isVisited[i]) {
				System.out.println("遍历到了" + i + "顶点");
				depthFirstSearch(i);
			}

	}

	// 对外提供的广度优先遍历
	public void broadFirstSearch() {
		// 假如图为有向图-----可能遍历到一定程度就再也走不通了
		// 如我例子中的节点2---所以需要对每一个节点进行一下循环
		for (int i = 0; i < vertexSize; i++)
			if (!isVisited[i]) {
				broadFirstSearch(i);
			}

	}

	private void broadFirstSearch(int i) {
		Queue<Integer> queue = new LinkedList<>();
		// 将遍历到的i压人队列中
		queue.add(i);
		isVisited[i] = true; // 标记该顶点已经被遍历过
		System.out.println("遍历到了" + i + "顶点");
		while (!queue.isEmpty()) {
			// 弹出队首的元素
			Integer head = queue.poll();
			// 获取队首元素第一个邻接点的元素
			int FN = getFirstNeighbor(head);
			while (FN != -1) { // 如果有第一个邻接点
				if (!isVisited[FN]) {// 且该邻接点没有被访问过
					isVisited[FN] = true;// 标记该顶点已经被遍历过
					System.out.println("遍历到了" + FN + "顶点");
					queue.add(FN); // 让FN进人队列
				}
				// 遍历队列首元素head基于FN的下一个元素
				FN = getNextNeighbor(head, FN);
			}
		}

	}

	public static void main(String[] args) {
		Graph graph = new Graph(6);
		int[] v0 = { 0, 4, MAX_WEIGHT, 7, 2, MAX_WEIGHT };
		int[] v1 = { MAX_WEIGHT, 0, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 3 };
		int[] v2 = { MAX_WEIGHT, 9, 0, 5, 6, MAX_WEIGHT };
		int[] v3 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 0, MAX_WEIGHT, MAX_WEIGHT };
		int[] v4 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 0, MAX_WEIGHT };
		int[] v5 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 1, 0 };

		graph.matrix[0] = v0;
		graph.matrix[1] = v1;
		graph.matrix[2] = v2;
		graph.matrix[3] = v3;
		graph.matrix[4] = v4;
		graph.matrix[5] = v5;
		// 深度优先遍历测试
		// graph.depthFirstSearch(); // 0 1 5 4 3 2

		// 广度优先遍历测试
		graph.broadFirstSearch();// 0 1 3 4 5 2
	}
}