潜在语义分析——统计学时代NLP的经典方法
文章目录
- 基本概要
- 单词向量空间
- 话题向量空间
- 基础概要
- 文本在话题向量空间的表示
- 从单词向量空间到话题向量空间的线性变换
- 潜在语义分析算法
- 非负矩阵分解算法
基本概要
潜在语义分析,简称LSA(Latent semantic analysis),1990年提出,是一种无监督学习方法,主要用于文本的话题分析、信息检索、推荐系统、图像处理等等。其特点是通过矩阵分解发现文本与单词之间的基于话题的语义关系。
文本信息处理中,传统方法以词向量表示文本的语义内容,以单词向量空间的度量表示文本之间的语义相似度。而这样的方式真的可以准确表示语义吗?不能(当时应该还是词袋模型one-hot表示法或频率统计或者共现矩阵,word2vec之后基本上可以满足,即使有的场景不满足也是要基于向量来更改,因为计算机内的运算只能流淌数据)。潜在语义分析就旨在解决这个问题,试图从大量的文本数据中发现潜在的话题,以话题向量表示文本的语义内容,以话题向量空间的度量更准确地表示文本之间的语义相似度。这也是话题分析的基本想法。
潜在语义分析使用的是非概率的话题分析模型。就是将文本集合表示为单词-文本矩阵,对单词-文本矩阵进行奇异值分解,从而得到话题向量空间,以及文本在话题向量空间的表示。
单词向量空间
向量空间模型的基本想法是,给定一个文本,用向量表示该文本的语义,向量的每一维对应一个单词,其数值为单词在该文本中出现的频数或权值(或tf-idf值)。假设文本中所有的单词的出现情况表示了文本的语义内容,文本集合中的每段文本都表示为一个向量存在于向量空间,那么内积或标准化内积就表示文本之间的语义相似度。
比如文本信息检索,用户提出查询时,帮助用户找到与查询最相关的文本,以排序的形式展示给用户。最简单的做法就是采用向量空间模型,将查询与文本表示为单词的向量,计算查询向量与文本向量的内积作为语义相似度。
统计学习方法中对单词-文本矩阵的严格定义如下:

而计算权值或者频率可能采用的tf-idf,可参考之前写的通俗解释TF-IDF这篇博客。
上面单词文本矩阵的第j列向量 x j x_j xj就表示了文本 d j d_j dj
x j = [ x 1 j x 2 j ⋮ x m j ] , j = 1 , 2 , ⋯ , n x_{j}=\left[\begin{array}{c} x_{1 j} \\ x_{2 j} \\ \vdots \\ x_{m j} \end{array}\right], \quad j=1,2, \cdots, n xj=⎣⎢⎢⎢⎡x1jx2j⋮xmj⎦⎥⎥⎥⎤,j=1,2,⋯,n
其中 x i j x_{ij} xij就表示了单词 w i w_i wi在文本 d j d_j dj的权值,权值越大,该单词在文本中的重要度就越高。
两个单词向量的内积或标准化内积表示对应的文本之间的语义相似度。因此,文本 d i d_i di和 d j d_j dj之间的相似度有如下两种度量方式:
x i ⋅ x j , x i ⋅ x j ∥ x i ∥ ∥ x j ∥ x_{i} \cdot x_{j}, \quad \frac{x_{i} \cdot x_{j}}{\left\|x_{i}\right\|\left\|x_{j}\right\|} xi⋅xj,∥xi∥∥xj∥xi⋅xj
从直观上确实解释得通,两个文本中共同出现的单词越多,且共同出现的单词在文本中的重要程度越相似,那么其语义内容就越接近,于是标准化内积就越大(这里不说内积,是因为同一个词在文档a里面十分重要,但在文档b里面一般重要,这样乘出来的内积会比在文档a和文档b都一般重要的内积要大,但显然后者才更加具备语义相似,所以衡量两个向量各维是否贴近仍然是标准化内积最合适,除非是one-hot表示法)
话题向量空间
基础概要
所谓话题,并没有严格的定义,就是指文本讨论的内容或主题。一个文本一般有若干个话题,如果两个文本的话题相似,那么两者的语义应该也相似。
如果定义一种话题向量空间模型,在给定一段文本的时候,用话题空间的里面的一个向量表示该文本,该向量的每一分量对应一个话题,其数值为该话题在文本中出现的权值。这样就能度量相似度了。而且话题的个数也远远小于单词的个数,这就是一种优化,代价就是话题很抽象,得到的难度提升了。其实潜在语义分析就是构建话题向量空间的方法。计算力允许的情况下,单词向量空间模型与话题向量空间模型可互为补充,同时使用。
接下来就要定义话题向量空间了。
首先还是重复一下单词向量空间的定义:

现在假设所有文本共含有k个话题。假设每个话题由一个定义在单词集合W上的m维向量表示,称为话题向量,即
t l = [ t 1 l t 2 l ⋮ t m l ] , l = 1 , 2 , ⋯ , k t_{l}=\left[\begin{array}{c} t_{1 l} \\ t_{2 l} \\ \vdots \\ t_{m l} \end{array}\right], \quad l=1,2, \cdots, k tl=⎣⎢⎢⎢⎡t1lt2l⋮tml⎦⎥⎥⎥⎤,l=1,2,⋯,k
其中 t i l t_{il} til就是单词 w i w_i wi在话题 t l t_l tl的权值,权值越大,该单词在话题中的重要度就越高。这k个话题向量张成了一个话题向量空间,维数为k。话题向量空间T是单词向量空间X的一个子空间(子集)。
这个子空间也就是话题向量空间可以这样表示:
T = [ t 11 t 12 ⋯ t 1 k t 21 t 22 ⋯ t 2 k ⋮ ⋮ ⋮ t m 1 t m 2 ⋯ t m k ] T=\left[\begin{array}{cccc} t_{11} & t_{12} & \cdots & t_{1 k} \\ t_{21} & t_{22} & \cdots & t_{2 k} \\ \vdots & \vdots & & \vdots \\ t_{m 1} & t_{m 2} & \cdots & t_{m k} \end{array}\right] T=⎣⎢⎢⎢⎡t11t21⋮tm1t12t22⋮tm2⋯⋯⋯t1kt2k⋮tmk⎦⎥⎥⎥⎤
文本在话题向量空间的表示
考虑文本集合D的文本 d j d_j dj,在单词向量空间中由一个向量 x j x_j xj表示,将 x j x_j xj投影到话题向量空间T中,得到在话题向量空间的一个k维向量 y j y_j yj(其实就是表示单词的m个向量,取一部分线性组合之后形成的k个新向量张成的空间B,再从空间B中取n个新向量,B就是话题向量空间,取出的新向量就组成话题-文本矩阵)。某次从空间A(m个单词张成的向量空间)中取出(怎么取就和权值计算方法有关了)的向量 x j x_j xj(也就是文本 d j d_j dj的单词向量表示),投影到空间B中的结果 y j y_j yj(也就是文本的话题向量表示)表达式为
y j = [ y 1 j y 2 j ⋮ y k j ] , j = 1 , 2 , ⋯ , n y_{j}=\left[\begin{array}{c} y_{1 j} \\ y_{2 j} \\ \vdots \\ y_{k j} \end{array}\right], \quad j=1,2, \cdots, n yj=⎣⎢⎢⎢⎡y1jy2j⋮ykj⎦⎥⎥⎥⎤,j=1,2,⋯,n
这里的 y l j y_{lj} ylj就是文本 d j d_j dj在话题 t l t_l tl的权值,权值越大,该话题在该文本中的重要度就越高。
下面的矩阵Y表示话题在文本中出现的情况,叫做话题-文本矩阵:
Y = [ y 11 y 12 ⋯ y 1 n y 21 y 22 ⋯ y 2 n ⋮ ⋮ ⋮ y k 1 y k 2 ⋯ y k n ] Y=\left[\begin{array}{cccc} y_{11} & y_{12} & \cdots & y_{1 n} \\ y_{21} & y_{22} & \cdots & y_{2 n} \\ \vdots & \vdots & & \vdots \\ y_{k 1} & y_{k 2} & \cdots & y_{k n} \end{array}\right] Y=⎣⎢⎢⎢⎡y11y21⋮yk1y12y22⋮yk2⋯⋯⋯y1ny2n⋮ykn⎦⎥⎥⎥⎤
从单词向量空间到话题向量空间的线性变换
表示单词的m个向量张成的空间A,形成单词向量空间,从A中取n个新向量,取出的新向量统称为单词-文本矩阵。
根据上一节的描述,其实从单词向量空间到话题向量空间之间是存在固定的映射关系的,怎么确立这种映射关系呢?
其实,两个空间的联系存在于,文本向量 d j d_j dj是同样的。 d j d_j dj在话题空间中的表示是 y j y_j yj,在单词空间中的表示是 x j x_j xj,所以有
x j ≈ y 1 j t 1 + y 2 j t 2 + ⋯ + y k j t k , j = 1 , 2 , ⋯ , n x_{j} \approx y_{1 j} t_{1}+y_{2 j} t_{2}+\cdots+y_{k j} t_{k}, \quad j=1,2, \cdots, n xj≈y1jt1+y2jt2+⋯+ykjtk,j=1,2,⋯,n
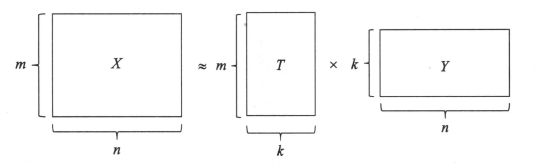
这个等式存在,空间的构建才是合理的,表明两者都表示完整了相似的语义。所以单词-文本矩阵X和单词-话题矩阵T以及话题-文本矩阵Y的关系为:
X ≈ T Y X \approx T Y X≈TY
这就是潜在语义分析。
在原始的单词向量空间中,两个文本 d i d_i di与 d j d_j dj的相似度可以由对应向量 x i x_i xi, x j x_j xj的标准化内积表示。而经过潜在语义分析之后,在话题向量空间中,两个文本 d i d_i di与 d j d_j dj的相似度可以由对应的向量标准化内积 y i y_i yi, y j y_j yj表示。
总结一下,要进行潜在语义分析,需要同时决定两部分的内容,一是话题向量空间T,二是文本你在话题空间的表示Y,使两者的乘积是原始矩阵数据的近似,而这一结果完全从话题-文本矩阵的信息中获得。
潜在语义分析算法
潜在语义分析算法利用的主要手段就是矩阵的奇异值分解,具体就是对单词-文本矩阵(也就是上面的X)进行奇异值分解,将其左矩阵作为话题向量空间(T),将其对角矩阵与右矩阵的乘积作为文本在话题向量空间的表示(Y)。
潜在语义分析根据确定的话题个数对单词-文本矩阵X进行截断奇异值分解:
X ≈ U k Σ k V k T = [ u 1 u 2 ⋯ u k ] [ σ 1 0 0 0 0 σ 2 0 0 0 0 ⋱ 0 0 0 0 σ k ] [ v 1 T v 2 T ⋮ v k T ] X \approx U_{k} \Sigma_{k} V_{k}^{\mathrm{T}}=\left[\begin{array}{llll} u_{1} & u_{2} & \cdots & u_{k} \end{array}\right]\left[\begin{array}{cccc} {\sigma}_{1} & 0 & 0 & 0 \\ 0 & \sigma_{2} & 0 & 0 \\ 0 & 0 & \ddots & 0 \\ 0 & 0 & 0 & \sigma_{k} \end{array}\right]\left[\begin{array}{c} v_{1}^{\mathrm{T}} \\ v_{2}^{\mathrm{T}} \\ \vdots \\ v_{k}^{\mathrm{T}} \end{array}\right] X≈UkΣkVkT=[u1u2⋯uk]⎣⎢⎢⎡σ10000σ20000⋱0000σk⎦⎥⎥⎤⎣⎢⎢⎢⎡v1Tv2T⋮vkT⎦⎥⎥⎥⎤
上式中 k ⩽ n ⩽ m k \leqslant n \leqslant m k⩽n⩽m。
有关奇异值算法有不明白的地方可参考之前写的这篇博客全面理解奇异值分解。
U矩阵的每一列 u k u_k uk都表示一个话题,称为话题向量。这k个话题张成的子空间称为话题向量空间:
U k = [ u 1 u 2 ⋯ u k ] U_{k}=\left[\begin{array}{llll} u_{1} & u_{2} & \cdots & u_{k} \end{array}\right] Uk=[u1u2⋯uk]
矩阵X的第j列向量 x j x_j xj就可以表示为
x j ≈ U k ( Σ k V k T ) j = [ u 1 u 2 ⋯ u k ] [ σ 1 v j 1 σ 2 v j 2 ⋮ σ k v j k ] = ∑ l = 1 k σ l v j l u l , j = 1 , 2 , ⋯ , n \begin{aligned} x_{j} &\approx U_{k}\left(\Sigma_{k} V_{k}^{\mathrm{T}}\right)_{j} \\ &=\left[\begin{array}{cccc} u_{1} & u_{2} & \cdots & u_{k} \end{array}\right]\left[\begin{array}{c} \sigma_{1} v_{j 1} \\ \sigma_{2} v_{j 2} \\ \vdots \\ \sigma_{k} v_{j k} \end{array}\right] \\ &=\sum_{l=1}^{k} \sigma_{l} v_{j l} u_{l}, \quad j=1,2, \cdots, n \end{aligned} xj≈Uk(ΣkVkT)j=[u1u2⋯uk]⎣⎢⎢⎢⎡σ1vj1σ2vj2⋮σkvjk⎦⎥⎥⎥⎤=l=1∑kσlvjlul,j=1,2,⋯,n
对角阵和V合并后的矩阵Y其实就是V的每一行乘以对应对角元素的倍数。上式的结果其实就是一段文本 d j d_j dj语义的近似表达式,也就是k个话题向量u的线性组合。Y的每一个列向量表示如下
[ σ 1 v 11 σ 2 v 12 ⋮ σ k v 1 k ] , [ σ 1 v 21 σ 2 v 22 ⋮ σ k v 2 k ] , ⋯ , [ σ 1 v n 1 σ 2 v n 2 ⋮ σ k v n k ] \left[\begin{array}{c} \sigma_{1} v_{11} \\ \sigma_{2} v_{12} \\ \vdots \\ \sigma_{k} v_{1 k} \end{array}\right],\left[\begin{array}{c} \sigma_{1} v_{21} \\ \sigma_{2} v_{22} \\ \vdots \\ \sigma_{k} v_{2 k} \end{array}\right], \cdots,\left[\begin{array}{c} \sigma_{1} v_{n 1} \\ \sigma_{2} v_{n 2} \\ \vdots \\ \sigma_{k} v_{n k} \end{array}\right] ⎣⎢⎢⎢⎡σ1v11σ2v12⋮σkv1k⎦⎥⎥⎥⎤,⎣⎢⎢⎢⎡σ1v21σ2v22⋮σkv2k⎦⎥⎥⎥⎤,⋯,⎣⎢⎢⎢⎡σ1vn1σ2vn2⋮σkvnk⎦⎥⎥⎥⎤
非负矩阵分解算法
非负矩阵分解算法也可以用于话题分析。对单词-文本矩阵进行非负矩阵分解,将其左矩阵作为话题向量空间,右矩阵作为文本在话题向量空间的表示。
