SparkGraphX介绍

1 并行图计算

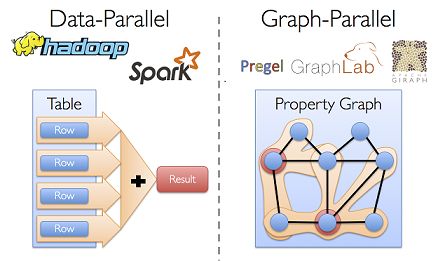
从社交网络到自然语言建模，图数据的规模和重要性已经促进了许多并行图系统的发展（例如Giraph和GraphLab等）。通过限制可描述的计算类型以引入新的划分图的方法，这些图计算模型可以有效地执行复杂的图算法，效率远远高于更通用的数据并行系统。下图比较了常见的数据并行模型和图并行模型。

分布式图计算框架的目的，就是将对于巨型图的各种操作，包装为简单的接口，让分布式存储，并行计算等复杂问题对上层透明。从而使得复杂网络和图算法的工程师，可以更加聚焦在图相关的模型设计和使用上，而不用关心底层的分布式细节

2 图数据库和Spark GraphX

图形数据库：是NoSQL数据库的一种类型，它应用图形理论存储实体之间的关系信息，有自己的查询语言，现在有几十种图查询语言，数据库的接口比较弱，只支持简单的查询。

GraphX：是一个计算引擎，提供了强大的计算接口，可以很方便的处理复杂的业务逻辑。

3 发展历程

 早在 0.5 版本，Spark 就带了一个小型的Bagel 模块，提供了类似 Pregel 的功能。这个版本还非常原始，性能和功能都比较弱，属于实验型产品。

 到 0.8 版本时，鉴于业界对分布式图计算的需求日益见涨，Spark 开始独立一个分支Graphx-Branch，作为独立的图计算模块，借鉴 GraphLab，开始设计开发 GraphX。

 在 0.9 版本中，这个模块被正式集成到主干，虽然是 Alpha 版本，但已可以试用，小面包圈Bagel 告别舞台。1.0 版本，GraphX 正式投入生产使用。现在spark的版本已更新到2.3.0

4 存储模式

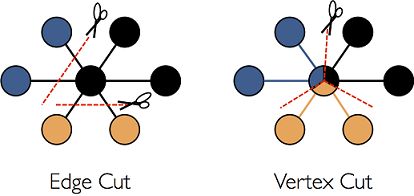
巨型图的存储总体上有边分割和点分割两种存储方式。2013 年，GraphLab2.0 将其存储方式由边分割变为点分割，在性能上取得重大提升，目前基本上被业界广泛接受并使用。

边分割（Edge-Cut）：每个顶点都存储一次，但有的边会被打断分到两台机器上。这样做的好处是节省存储空间；坏处是对图进行基于边的计算时，对于一条两个顶点被分到不同机器上的边来说，要跨机器通信传输数据，内网通信流量大。

点分割（Vertex-Cut）：每条边只存储一次，都只会出现在一台机器上。邻居多的点会被复制到多台机器上，增加了存储开销，同时会引发数据同步问题。好处是可以大幅减少内网通信量。

虽然两种方法互有利弊，但现在是点分割占上风，各种分布式图计算框架都将自己底层的存储形式变成了点分割。主要原因有以下两个：

1. 磁盘价格下降，存储空间不再是问题，而内网的通信资源没有突破性进展，集群计算时内网带宽是宝贵的，时间比磁盘更珍贵。这点就类似于常见的空间换时间的策略。
2. 在当前的应用场景中，绝大多数网络都是“无尺度网络”，遵循幂律分布，不同点的邻居数量相差非常悬殊。而边分割会使那些多邻居的点所相连的边大多数被分到不同的机器上，这样的数据分布会使得内网带宽更加捉襟见肘，于是边分割存储方式被渐渐抛弃了。

Graphx 借鉴 PowerGraph，使用的是Vertex-Cut(点分割)方式存储图，用三个 RDD 存储图

数据信息：

 VertexTable(id, data)：id 为 Vertex id，data 为 Edge data

 EdgeTable(pid, src, dst, data)：pid 为 Partion id，src 为原定点 id，dst 为目的顶点 id

 RoutingTable(id, pid)：id 为 Vertex id，pid 为 Partion id

点分割存储实现如下图所示：

5  图计算模式

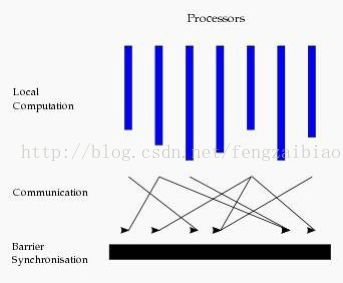
目前基于图的并行计算框架已经有很多，比如来自 Google 的 Pregel、来自 Apache 开源的图计算框架 Giraph/HAMA 以及最为著名的 GraphLab，其中 Pregel、HAMA 和 Giraph 都是非常类似的，都是基于 BSP（Bulk Synchronous Parallell）模式，Spark GraphX也是。

Bulk Synchronous Parallell，即整体同步并行计算模型，它将计算分成一系列的超步（superstep，每一轮的迭代叫做一个超步）的迭代（iteration）。从纵向上看，它是一个串行模式，而从横向上看，它是一个并行的模式，每两个 superstep 之间设置一个栅栏（barrier），即整体同步点，确定所有并行的计算都完成后再启动下一轮 superstep。

每一个超步（superstep）包含三部分内容：

1. 计算 compute：每一个processor 利用上一个 superstep 传过来的消息和本地的数据进行本地计算；
2. 消息传递：每一个 processor 计算完毕后，将消息传递个与之关联的其它 processors；
3. 整体同步点：用于整体同步，确定所有的计算和消息传递都进行完毕后，进入下一个superstep。

6 图状态更新

基于上述BSP编程模型，google开发了pregel，apache开发了类似的项目：HAMA。现在Spark GraphX中也提供了pregel接口。首先看pregel中状态机，如下图所示。

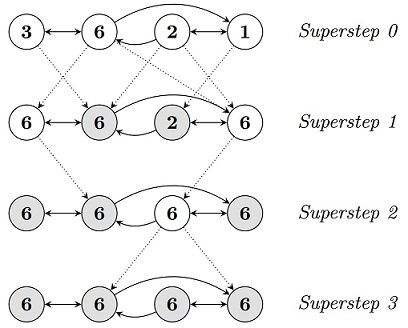
在Pregel中，以节点为计算单元。初始时，每个节点都是活动节点。一个节点通过“voting to halt”来使自身失效。这意味着失效点不再计算除非外部触发。也即在后续superstep中，pregel不计算失效点，直到失效点接收到消息。收到消息后并处理后，节点必须再次使自身失效。当图中所有点失效并且没有消息传递，算法结束。

下图使用一个简单的例子-求最大值，来解释上诉过程。

• superstep 0中，每个节点都是活动点，且向邻居节点传递自身属性值。
• 节点接受到邻居节点属性值后，更新当前节点属性值为当前已知最大值。需要更新值的节点保持活动状态，无需更新值的节点自动转入 失效状态。
• 重复这个过程，直到图中不存在活动节点且没有消息传递。

最后得到图中最大值为6。

6 graphx举例说明

定义用户(id,(name,age)),粉丝关系Edge(idFans,idStar,degree)

统计比自己年纪大的粉丝数及其平均年龄

import org.apache.spark.SparkConf
import org.apache.spark.SparkContext
import org.apache.spark._
import org.apache.spark.graphx._
import org.apache.spark.rdd.RDD

object myGraphX {

  def main(args: Array[String]) {

    val sparkConf = new SparkConf().setAppName("myGraphPractice").
          setMaster("local[2]")
    val sc = new SparkContext(sparkConf)

    // 顶点RDD[顶点的id,顶点的属性值]
    val users: RDD[(VertexId, (String, Int))] = sc.parallelize(Array((4L, ("David", 18)),
      (1L, ("Alice", 28)), (6L, ("Fran", 40)),(3L, ("Charlie", 30)), (2L, ("Bob", 70)), (5L, ("Ed", 55))))

    val relationships: RDD[Edge[Int]] = sc.parallelize(Array(Edge(4L, 2L, 2),
        Edge(2L, 1L, 7), Edge(4, 5, 8), Edge(2, 4, 2),Edge(5, 6, 3), Edge(3, 2, 4),
        Edge(6, 1, 2), Edge(3, 6, 3), Edge(6, 2, 8), Edge(4, 1, 1), Edge(6, 4, 3)))
    // 默认（缺失）用户
    val defaultUser = ("John Doe", 0)

    //使用RDDs建立一个Graph（有许多建立Graph的数据来源和方法，后面会详细介绍）
    val graph = Graph(users, relationships, defaultUser)

    //定义一个相邻聚合，统计比自己年纪大的粉丝数（count）及其平均年龄（totalAge/count)
    val olderFollowers = graph.aggregateMessages[(Int, Int)](
      triplet => {
        if (triplet.srcAttr._2 > triplet.dstAttr._2) {
          triplet.sendToDst((1, triplet.srcAttr._2))
        }
      },
      (a, b) => (a._1 + b._1, a._2 + b._2), //(2)相当于Reduce函数，a，b各代表一个元组（count，Age）
      TripletFields.All) //(3)可选项,TripletFields.All/Src/Dst

    //计算平均年龄
    val averageOfOlderFollowers = olderFollowers.mapValues(
      (id, value) => value match {
        case (count, totalAge) => (count, totalAge / count)
    })

    averageOfOlderFollowers.foreach(println)
  }
}

输出结果：
(4,(2,55))
(1,(2,55))
(6,(1,55))

7 pregel 操作计算过程分析

graphx中只用了几十行代码实现pregel计算过程

class GraphOps[VD, ED] {

  def pregel[A]
      (initialMsg: A,//在第一次迭代的时候顶点收到的消息
       maxIter: Int = Int.MaxValue,//最大迭代数
       activeDir: EdgeDirection = EdgeDirection.Out)
      (vprog: (VertexId, VD, A) => VD,
      sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexId, A)],
      mergeMsg: (A, A) => A)
    : Graph[VD, ED] = {

    var g = mapVertices( (vid, vdata) => vprog(vid, vdata, initialMsg) ).cache()

    var messages = g.mapReduceTriplets(sendMsg, mergeMsg)
    var activeMessages = messages.count()
 
    var i = 0
    while (activeMessages > 0 && i < maxIterations) {
      g = g.joinVertices(messages)(vprog).cache()
      val oldMessages = messages

      messages = g.mapReduceTriplets(
        sendMsg, mergeMsg, Some((oldMessages, activeDirection))).cache()
      activeMessages = messages.count()
      i += 1
    }
    g
  }
}