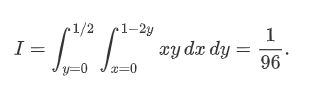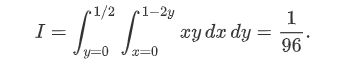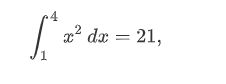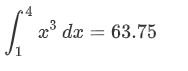python中scipy.intergrate的部分积分用法
scipy.integrate中提供了几种积分算法，使用help命令来获取该模块的简述
一般积分(quad)
quad提供了对一个函数一段距离（边界可以为正无穷或负无穷）内积分的功能。如下：对J2.5(x)函数在[0,4.5]范围内进行积分运算。
import scipy.integrate as integrate
import scipy.special as special
result = integrate.quad(lambda x: special.jv(2.5,x), 0, 4.5)
result=(1.1178179380783249, 7.8663172481899801e-09)
from numpy import sqrt, sin, cos, pi
I = sqrt(2/pi)*(18.0/27*sqrt(2)*cos(4.5) - 4.0/27*sqrt(2)*sin(4.5) +
sqrt(2*pi) * special.fresnel(3/sqrt(pi))[0])
>>>I=1.117817938088701
print(abs(result[0]-I))
1.03761443881e-11
quad的第一个参数是一个“可调用的”python对象（即函数，方法或类实例）。注意在这种情况下使用lambda函数作为参数。接下来的两个参数是集成的极限。返回值是一个元组，第一个元素保存积分的估计值，第二个元素保存误差的上限。注意，在这种情况下，该积分的真实值为
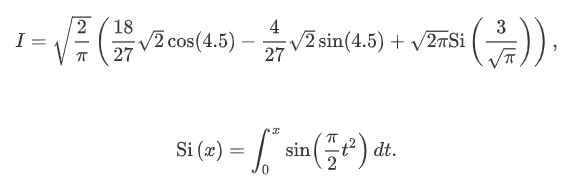
Si(x)是菲涅耳正弦积分。
如果被积分函数中有其他参数需要设定，我们可以通过以下方法来处理。例如：
from scipy.integrate import quad
def integrand(x, a, b):
return a*x**2 + b
a = 2
b = 1
I = quad(integrand, 0, 1, args=(a,b))
>>> I
(1.6666666666666667, 1.8503717077085944e-14)
也可以对边界为无穷的函数进行积分，也可以使用special.expn定义一个基于quad的函数“vec_expint”例如：
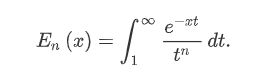
from scipy.integrate import quad
def integrand(t, n, x):
return np.exp(-x*t) / t**n
vec_expint = np.vectorize(expint)
vec_expint(3, np.arange(1.0, 4.0, 0.5))
>>>array([ 0.1097, 0.0567, 0.0301, 0.0163, 0.0089, 0.0049])
import scipy.special as special
special.expn(3, np.arange(1.0,4.0,0.5))
>>>array([ 0.1097, 0.0567, 0.0301, 0.0163, 0.0089, 0.0049])
也可以多次调用quad进行多重积分（有误差），例如：
result = quad(lambda x: expint(3, x), 0, np.inf)
print(result)
(0.33333333324560266, 2.8548934485373678e-09)
I3 = 1.0/3.0
print(I3)
(0.33333333324560266, 2.8548934485373678e-09)
print(I3 - result[0])
8.77306560731e-11
一般多重积分(dblquad,tplquad,nquad)
二重和三重积分已经被整合到dblquad和tplquad中了。这些函数采用分别集成和四个或六个参数的函数。所有内部积分的边界都需要定义为函数。使用双重积分来计算多个值的示例 In 如下图所示：
from scipy.integrate import quad, dblquad
def I(n):
return dblquad(lambda t, x: np.exp(-x*t)/t**n, 0, np.inf, lambda x: 1, lambda x: np.inf)
>>> print(I(4))
(0.2500000000043577, 1.29830334693681e-08)
>>> print(I(3))
(0.33333333325010883, 1.3888461883425516e-08)
>>> print(I(2))
(0.4999999999985751, 1.3894083651858995e-08)
当被积分函数的边界为函数时：
from scipy.integrate import dblquad
area = dblquad(lambda x, y: x*y, 0, 0.5, lambda x: 0, lambda x: 1-2*x)
>>>area
(0.010416666666666668, 1.1564823173178715e-16)
对于 In ，scipy提供了功能nquad。积分界限是一个可迭代的对象：常数界限的列表或非常数积分界限的函数的列表。积分的顺序（以及边界的顺序）从最里面的积分到最外面的积分。注意，f的参数顺序必须与积分边界的顺序匹配。
from scipy import integrate
N = 5
def f(t, x):
return np.exp(-x*t) / t**N
integrate.nquad(f, [[1, np.inf],[0, np.inf]])
(0.20000000000002294, 1.2239614263187945e-08)
from scipy import integrate
def f(x, y):
return x*y
def bounds_y():
return [0, 0.5]
def bounds_x(y):
return [0, 1-2*y]
integrate.nquad(f, [bounds_x, bounds_y])
高斯正交
还提供了一些功能，以便在固定间隔内执行简单的高斯求积。第一个是fixed_quad执行固定阶高斯正交。第二个功能是 quadrature执行多个阶数的高斯正交，直到积分估计值的差异低于用户提供的一定容差为止。这些函数都使用了模块scipy.special.orthogonal，该模块 可以计算各种正交多项式的根和正交权重（多项式本身可以作为返回多项式类实例的特殊函数提供，例如special.legendre）
使用样本进行集成
在任意间隔的样本的情况下，这两个函数trapz 和simps是可用的。他们分别使用1和2阶的Newton-Coates公式执行积分。梯形法则将函数近似为相邻点之间的直线，而辛普森法则将函数近似为三个相邻点之间的抛物线。
如果函数是3阶或更少阶的多项式，则对于奇数均等间隔的样本，Simpson规则是精确的。如果样本的间距不相等，则仅当函数为2阶或更小的多项式时，结果才是精确的。
import numpy as np
def f1(x):
return x**2
def f2(x):
return x**3
x = np.array([1,3,4])
y1 = f1(x)
from scipy.integrate import simps
I1 = simps(y1, x)
print(I1)
>>>21.0
等价于
而当阶数大于2时，此方法不可用。如图
y2 = f2(x)
I2 = integrate.simps(y2, x)
print(I2)
>>>61.5
使用低级回调函数更快的积分
希望减少的积分时间用户可以通过传递一个C函数指针scipy.LowLevelCallable到quad，dblquad， tplquad或nquad和其将被集成并在Python返回结果。这里的性能提高来自两个因素。主要的改进是更快的函数评估，这是由函数本身的编译提供的。此外，通过删除中的C和Python之间的函数调用，我们可以提高速度 quad。对于诸如正弦之类的微不足道的功能，此方法可以提供约2倍的速度改进，但对于更复杂的功能，可以产生更明显的改进（10x +）。然后，此功能面向具有大量数字积分的用户，他们愿意写一点C来显着减少计算时间。
例如，可以通过ctypes几个简单的步骤使用该方法：
1.）用函数签名在C中编写一个被积分函数 ，其中是一个数组，其中包含函数f的求值点，以及 要提供的任意其他数据。
2.）现在将此文件编译到共享/动态库中（由于它依赖于OS，因此快速搜索将对此有所帮助）。用户必须链接使用的所有数学库等。在linux上。输出库将称为testlib.so，但它可能具有不同的文件扩展名。现在已经创建了一个库，可以使用将该库加载到Python中ctypes。
3.）负载共享库成Python使用ctypes，并设置restypes和 argtypes-这允许SciPy的正确解释的功能
函数的最后一个是可选的，如果不需要，可以省略（在C函数和ctypes argtypes中）。请注意，坐标以双精度数组而不是单独的参数传递。void *user_data
4.）现在像往常一样集成库函数，在这里使用nquad：
