【搞定算法】KMP 算法
目 录:
1、问题描述
2、next 数组
3、代码实现
4、KMP 的应用
4.1、子树问题
4.2、加最短字符问题
前面讲过字符串匹配的其他几种算法:字符串匹配算法之 BF、RK、BM。
本文用来讲解 KMP 算法及其应用,KMP 算法时间复杂度为:O(N + M),空间复杂度为:O(M)。
1、问题描述
给定两个字符串 O 和 f,长度分别为 n 和 m,判断 f 是否在 O 中出现,如果出现则返回出现的位置。常规暴力方法是遍历 o 的每一个位置,然后从该位置开始和 f 进行匹配,但是这种方法的复杂度是 O(N x M)。KMP 算法通过一个 O(M) 的预处理(next 数组)可以加速匹配速度,使匹配的复杂度降为 O(N + M)。
2、next 数组
注意:next 数组是针对标准串而言的(上图中 f 是标准串、O 是母串)。
其实字符串匹配算法理解起来并不难,非常直观,结果就要求要匹配的字符在两个串中一一对应。但是为了提高暴力解法的效率,就必须提高字符串的匹配速度,其实就是解决每次匹配失败如何往前多移几位的问题,不要每次都是匹配失败,移动一位再重头开始。next 数组就是来做这件事情的,每次匹配失败,查找匹配串匹配失败位置处对应的 next 值,标准串向前移动 next 值那么多的长度,然后再继续和母串匹配。
那下面就讲一下 next 数组究竟是什么:
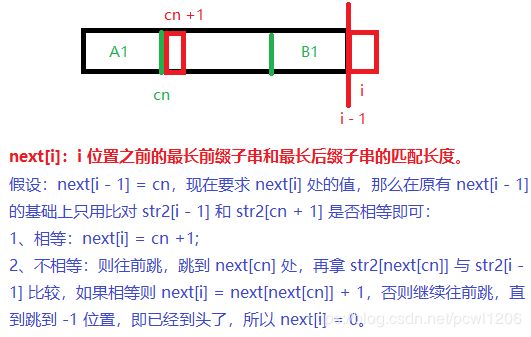
如上图所示:next 数组存放的是字符串 f 的 i 位置前面字符串的最长前缀和最长后缀的匹配长度【前缀不能扩到最后一个字符,后缀也不能扩到第一个字符】。
- A 段字符串是 f 在 i 位置的最长前缀子串;
- B 段字符串是 f 在 i 位置的最长后缀子串;
- A 段字符串和 B 段字符串相等。
分析:在字符串 O 中寻找 f,当匹配到位置 i 时两个字符串不相等,这时我们需要将字符串 f 向后移动。常规方法是每次向后移动 1 位,但是它没有考虑前 i - 1 位已经比较过这个事实,所以效率不高。KMP就是要加速这个过程:
- 前提:
1、在两个数组都没有越界的范围内(str1 是母串、str2 是标准串):
2、next[] 数组【存放 i 位置前面字符串的前缀和后缀的最长匹配长度】的求解方法
(1)next 数组下标为 0 的位置人为规定值为 - 1;
(2)next 数组下标为 1 的位置人为规定值为 0,因为前面只有一个字符,但前缀不能扩到最后一个字符,后缀也不能扩到第一个字符,所以人为规定为 0;
(3)求 i 位置的值,即 next[i] :利用前面的已得到的结果,cn 表示跳到的位置,即需要和 i-1 位置字符比较的位置
<1> str[cn] 和 str[i - 1] 相等,则得到结果 next[i++] = ++cn;
<2> 不相等就要继续往前面跳(跳到 next[cn] 处),直到有相等或者 cn = -1 没办法跳了。
- 过程:
1、如果 str1 的 p1 位置和 str2 的 p2 位置的值相等,则 p1++、p2++;
2、如果 str1 的 p1 位置和 str2 的 p2 位置的值不相等:
(1)如果 p2 已经是 0 位置了(next[p2] = -1),则 p2 就不能往前走了,需要 p1++ 【因为 str1 的当前位置和 str2 的 0位置都不匹配,所以str1 要到下一个位置】;
(2)否则 p2 = next[p2](next[p2] 是 p2 位置前面字符串的最长前缀和最长后缀的匹配长度,从新的 p2 位置开始和 str1 的当前位置比较下去,即图中的 A 的下一位和 a 继续比较);
- 实质:
1、尝试解决位置 j [O 中 B 的第一位] 开头能否匹配出 str2;
2、认为从 j 到 i 中间位置一律配不出 str2;
- 越界:
1、如果是 p2 越界,说明标准串 str2 已经遍历完了,即 str1 匹配出了 str2;
2、如果是 p1 越界,说明母串 str1 已经遍历完了也没有匹配出标准串 str1。
举例:
3、代码实现
public class KMP {
/**
* 主函数:返回 str2 在 str1 中第一次出现的位置
* @param str1 :母串
* @param str2 :标准串
* @return str2 在 str1 中第一次出现的位置
*/
public static int getIndexOf(String str1, String str2){
if(str1 == null || str2 == null || str2.length() < 1 || str1.length() < str2.length()){
return -1;
}
int p1 = 0; // str1的指针
int p2 = 0; // str2的指针
char[] s1 = str1.toCharArray();
char[] s2 = str2.toCharArray();
int[] next = getNextArray(s2);
// 循环结束一顶是有一个数组越界了,即遍历完了
while(p1 < str1.length() && p2 < str2.length()){
if(s1[p1] == s2[p2]){
// 继续往后匹配,两个一起往后走
p1++;
p2++;
}else{
// 不相等的时候,就要利用next数组往前跳
if(next[p2] == -1){
//s2到0位置了,没办法往前跳了,而你s1当前位置和我的0位置都不匹配,s1得往后走一步
p1++;
}else{
p2 = next[p2];
}
}
}
// 只有是当p2越界跳出的循环,在str1中才会存在str2,否则不存在
return p2 == s2.length ? p1 - p2 : -1;
}
// 求 str2 的 next 数组
public static int[] getNextArray(char[] str2){
int[] next = new int[str2.length];
next[0] = -1; // 人为规定
if(str2.length == 1){
return next;
}
// 长度不止1时
next[1] = 0; // 人为规定
int i = 2; // 从左往右求每一个 i 的 next 值
/**cn 有两层意思:
* 1、cn 表示要跳到的位置,即需要和 i-1 位置处字符比较的位置
* 2、cn 就是 i-1 处的next值,即 i-1处的最长前缀和最长后缀的匹配值
*/
int cn = 0;
while(i < next.length){
if(str2[i-1] == str2[cn]){
//得到了 i 位置的next值,可以求i+1位置的next值了
next[i++] = ++cn;
}else{
// 不相等,就要往前跳,直到跳到next值为-1的位置,即0位置
if(next[cn] == -1){
// 不能再继续跳了,已经到0位置了,且0位置和i-1位置不相等
next[i++] = 0;
}else{
// 继续往前跳,继续比较
cn = next[cn];
}
}
}
return next;
}
public static void main(String[] args) {
String str = "abcabcababaccc";
String match = "ababa";
System.out.println(getIndexOf(str, match));
}
}时间复杂度分析:
1、getNextArray 函数的时间复杂度 O(M)。设 str2 的长度为 M ,分析其时间复杂度的困惑在于,在 while 里面不是每次循环都执行 ++i 操作,所以整个 while 的执行次数不一定为 M。换个角度,注意到在每次循环中,无论 if 还是 else 都会修改 cn 的值且每次循环仅对 cn 进行一次修改,所以在整个 while 中 cn 被修改的次数即为 getNextArray 函数的时间复杂度。
2、那么每次成功匹配时,++i; ++n; , 由于 ++i 最多执行 M-1 次,故 ++j 也最多执行 M-1 次,即 cn 最多增加 M-1 次。对应的,只有在 cn =next[cn] 处, cn 的值一定会变小,由于 cn 最多增加 M - 1 次,故 n 最多减小 M - 1 次。所以 时间复杂度为 2M。
3、综上所述:getNextArray 函数的时间复杂度为 O(M),若母串长度为 M,标准串长度为 N,则 KMP 的时间复杂度为:O(M + N)。
4、KMP 的应用
4.1、子树问题
问题:T2 是不是 T1 的子树,即 T1 的某棵子树完全和 T2 一样,就说 T1 包含 T2。
分析:把 T1 先序遍历,序列化为字符串,把 T2 也序列化为字符串,利用 KMP 算法如果前者包含后者,则说明 T1 包含 T2。
public class SubTree {
public static class Node{
public int val;
public Node left;
public Node right;
public Node(int val){
this.val = val;
}
}
public static boolean isSubTree(Node T1, Node T2){
String t1Str = serialByPre(T1);
String t2Str = serialByPre(T2);
return getIndexOf(t1Str, t2Str) != -1;
}
public static String serialByPre(Node root){
if(root == null){
return "#_";
}
String res = root.val + "_";
res += serialByPre(root.left);
res += serialByPre(root.right);
return res;
}
public static int getIndexOf(String str1, String str2){
if(str1 == null || str2 == null || str2.length() < 1 || str1.length() < str2.length()){
return -1;
}
int p1 = 0; // str1的指针
int p2 = 0; // str2的指针
char[] s1 = str1.toCharArray();
char[] s2 = str2.toCharArray();
int[] next = getNextArray(s2);
// 循环结束一顶是有一个数组越界了,即遍历完了
while(p1 < str1.length() && p2 < str2.length()){
if(s1[p1] == s2[p2]){
// 继续往后匹配,两个一起往后走
p1++;
p2++;
}else{
// 不相等的时候,就要利用next数组往前跳
if(next[p2] == -1){
//s2到0位置了,没办法往前跳了,而你s1当前位置和我的0位置都不匹配,s1得往后走一步
p1++;
}else{
p2 = next[p2];
}
}
}
// 只有是当p2越界跳出的循环,在str1中才会存在str2,否则不存在
return p2 == s2.length ? p1 - p2 : -1;
}
// 求 str2 的 next 数组
public static int[] getNextArray(char[] str2){
int[] next = new int[str2.length];
next[0] = -1;
if(str2.length == 1){
return next;
}
// 长度不止1时
next[1] = 0;
int i = 2;
int cn = 0;
while(i < next.length){
if(str2[i-1] == str2[cn]){
next[i++] = ++cn;
}else{
if(next[cn] == -1){
next[i++] = 0;
}else{
cn = next[cn];
}
}
}
return next;
}
}
4.2、加最短字符问题
问题:给定一个字符串,如何在字符串后面加最短的字符(只能在原始串的后面进行添加)使其构成一个长的字符串且包含两个原始字符串。
分析:其实需要加的字符串就是原字符串的最长前后缀子串。那么就是和 next 数组相关的问题了:
举例:abcabc --> abcabcabc 最少增加 3 个。
- 在 KMP 中 next 数组基础上多求一位终止位,图中最后一位 x 的 next 值为 5,但是前 4 个可以复用,将缺少的 a 补上即可。
public class ShortestHaveTwice {
public static String getAddStr(String str){
if(str == null || str.length() == 0){
return "";
}
char[] chars = str.toCharArray();
if(chars.length == 1){
return str + str;
}
if(chars.length == 2){
return chars[0] == chars[1] ? (str + String.valueOf(chars[0])) : (str + str);
}
int endNext = getEndNextLength(chars);
return str += str.substring(endNext);
}
public static int getEndNextLength(char[] chars){
// 多求一个终止位的next值
int[] next = new int[chars.length + 1];
next[0] = -1;
next[1] = 0;
int i = 2;
int cn = 0;
while(i < next.length){
if(chars[i-1] == chars[cn]){
next[i++] = ++cn;
}else{
if(next[cn] == -1){
next[i++] = 0;
}else{
cn = next[cn];
}
}
}
return next[next.length - 1];
}
public static void main(String[] args) {
String str1 = "a";
System.out.println("str1 --> " + getAddStr(str1));
String str2 = "aa";
System.out.println("str2 --> " + getAddStr(str2));
String str3 = "ab";
System.out.println("str3 --> " + getAddStr(str3));
String str4 = "abcabc";
System.out.println("str4 --> " + getAddStr(str4));
}
}