Python-科赫雪花（科克曲线）

翻译过来的名字，WHO CARE

---

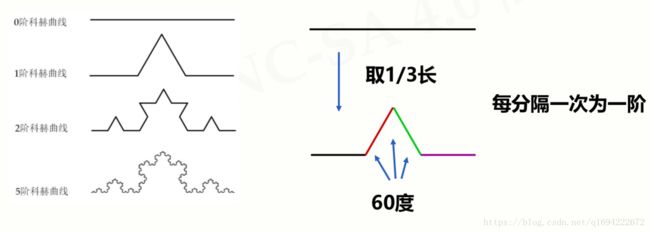
定义

设想一个边长为1的等边三角形，取每边中间的三分之一，接上去一个形状完全相似的但边长为其三分之一的三角形，结果是一个六角形。现在取六角形的每个边做同样的变换，即在中间三分之一接上更小的三角形，以此重复，直至无穷。外界的变得原来越细微曲折，形状接近理想化的雪花。它的名字叫科克曲线

---

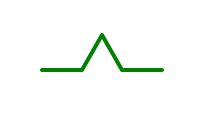
首先绘制科克曲线

科克曲线很简单

#科克曲线
import turtle
turtle.pensize(4)
turtle.pencolor('green')
turtle.penup()
turtle.goto(-100,0)
turtle.pendown()

#抽象步骤，如果是0阶，只需前行；如果是一阶，需要前行，转向，前行，转向，前行，转向，前行，
#共有的是前行，阶数需要控制转向的次数，所以边界是0阶，只需前行
def keke_line(n=1,len=120):
    if n==0:
        turtle.fd(len)
    else:
        for i in [0,60,-120,60]:
            turtle.left(i)
            keke_line(n-1,len/3)

keke_line()


turtle.hideturtle()
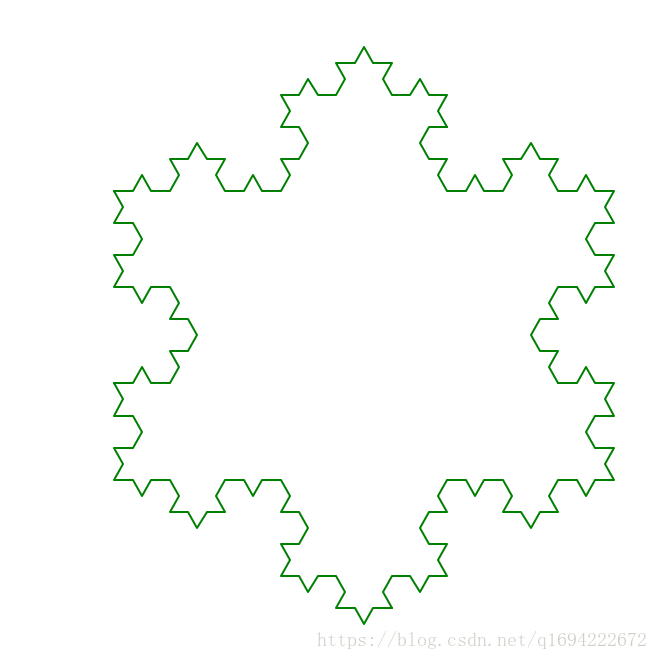
turtle.done()

---

❄️雪花就很好办了

#科赫雪花
import turtle

def kehe(len,n):
    if n == 0:
        turtle.fd(len)
    else:
        for i in [0,60,-120,60]:
            turtle.left(i)
            kehe(len / 3, n - 1)


lenth = 500
level = 3
du = 120
def main():
    turtle.penup()
    turtle.goto(-100,100)
    turtle.pensize(2)
    turtle.color('green')
    turtle.pendown()

    kehe(lenth,level)
    turtle.right(du)
    kehe(lenth, level)
    turtle.right(du)
    kehe(lenth, level)
    turtle.right(du)




    turtle.hideturtle()
    turtle.done()

main()

这是三阶

这是五阶