卡尔曼滤波推导

本文为原创文章，转载请注明出处：https://blog.csdn.net/q_z_r_s

机器感知 一个专注于SLAM、三维重建、机器视觉等相关技术文章分享的公众号

卡尔曼滤波推导

1. 射影理论

卡尔曼滤波器是线性最小方差估计，也叫最优滤波器，再几何上，卡尔曼滤波估值是状态变量在由观测生成的线性空间上的射影。因此射影理论是卡尔曼滤波推到的基本工具。

1.1 线性最小方差估计和射影

【定义】由 $m\times 1$ 维随机变量 $y\in R^m$ 的线性函数估计 $n\times 1$ 维随机变量 $x\in R^n$ ，记估值为
$$\hat{x}=b+Ay,b\in R^n,A\in R^{n\times m}\text{\hspace{1em}(1.1)}$$
若估值 $\hat{x}$ 极小化性能指标为 $J=E[(x-\hat{x}{)}^T(x-\hat{x})]$ ，则称 $\hat{x}$ 为随机变量 $x$ 的线性最小方差估计。

将 $(1.1)$ 式代入极小化性能指标可得
$$J=E[(x-b-Ay{)}^T(x-b-Ay)]\text{\hspace{1em}(1.2)}$$
为了求性能指标极小值，分别求关于变量 $b$ 和变量 $A$ 的偏导数
$$\frac{\partial J}{\partial b}=-2E(x-b-Ay)=0\text{\hspace{1em}(1.3)}$$

$$\frac{\partial J}{\partial A}=-P_{yx}^T-P_{x}y+2A{P}_{yy}=0\text{\hspace{1em}(1.4)}$$

通过$(3)(4)$可解得
$$b=Ex-AEy\text{\hspace{1em}(1.5)}$$

$$A=P_{xy}{P}_{yy}^{-1}\text{\hspace{1em}(1.6)}$$

上述结果可概括为如下定理：

【定理】有随机变量 $y\in R^m$ 对随机变量 $x\in R^n$ 的线性最小方差估计公式为
$$\hat{x}=Ex+P_{xy}{P}_{yy}^{-1}(y-Ey)\text{\hspace{1em}(1.7)}$$
其中假设$Ex,Ey,P_{xy},P_{yy}$均存在。

【推论】无偏性$E\hat{x}=Ex$。

证明 $E\hat{x}=E[Ex+P_{xy}{P}_{yy}^{-1}(y-Ey)]=Ex+P_{xy}{P}_{yy}^{-1}(Ey-Ey)=Ex$

【推论】正交性$E[(x-\hat{x})y^T]=0$。

证明
$$\begin{gathered} E[(x-\hat{x})y^T]=E[(x-Ex-P_{xy}{P}_{yy}^{-1}(y-Ey))y^T=E[(x-\hat{x})(y-Ey{)}^T] \\ =E[(x-Ex-P_{xy}{P}_{yy}^{-1}(y-Ey))(y-Ey{)}^T]=P_{xy}-P_{xy}{P}_{yy}^{-1}{P}_{yy} \\ =P_{xy}-P_{xy}=0 \end{gathered}$$
其中，引入$E[(x-\hat{x}){Ey}^T]=0$做辅助计算。此推论表明，真实值与估值之差与$y$不相关，我们称$x-\hat{x}$与$y$不相关为$x-\hat{x}$与$y$正交(垂直)，记为$(x-\hat{x})\perp y$，并称$\hat{x}$为$x$在$y$上的射影，记为$\hat{x}=proj(x|y)$。

【定义】由$y(1),\cdot \cdot \cdot ,y(k)\in R^m$张成的线性流行$L(y(1),\cdot \cdot \cdot ,y(k))$定义为
$$\begin{gathered} L(y(1),\cdot \cdot \cdot ,y(k))\underline{\underline{\Delta }}L(w) \\ L(w)=y|y=Aw+b,\forall b\in R^n,\forall A\in R^{n\times km} \end{gathered}$$
引入分块矩阵
$$A=[A_1,\cdots ,A_k],A_i\in R^{n\times m}$$
则有
$$L(w)=y|y=\sum _{i=1}^k{A}_{i}y(i)+b,\forall A_i\in R^{n\times m},\forall b\in R^n=L(y(1),\cdot \cdot \cdot ,y(k))$$
【定义】基于随机变量 $y(1),\cdot \cdot \cdot ,y(k)\in R^m$ 对随机变量 $x\in R^n$ 的线性最小方差估计 $\hat{x}$ 定义为
$$\hat{x}=proj(x|w)=proj(x|y(1),\cdot \cdot \cdot ,y(k))$$
也称 $\hat{x}$ 为 $x$ 在线性流形 $L(w)$ 或 $L(y(1),\cdot \cdot \cdot ,y(k))$ 上的射影。

【推论】设 $x\in R^n$ 为零均值随机变量， $y(1),\cdot \cdot \cdot ,y(k)\in R^m$ 为零均值，互不相关(正交)的随机变量，则有
$$proj(x|y(1),\cdots ,y(k))=\sum _{i=1}^{k}proj(x|y(i))$$

1.2 新息序列

【定义】设 $y(1),\cdot \cdot \cdot ,y(k),\cdots \in R^m$ 是存在二阶矩的随机序列，它的新息序列(新息过程)定义为
$$ϵ(k)=y(k)-proj(y(k)|y(1),\cdots ,y(k-1)),k=1,2,\cdots$$
并定义 $y(k)$ 的一步最优预报估值为
$$\hat{y}(k|k-1)=proj(y(k)|y(1),\cdots ,y(k-1))$$
因而新息序列可定义为
$$ϵ(k)=y(k)-\hat{y}(k|k-1),k=1,2,\cdots$$
其中规定 $\hat{y}(1|0)=Ey(1)$ ，这保证 $Eϵ(1)=0$ 。新息序列的几何意义是
$$ϵ(k)\perp L(y(1),\cdot \cdot \cdot ,y(k-1))$$
且新息序列 $ϵ(k)$ 是零均值白噪声(这是产生递推射影公式的基础，通过引入新息序列实现了非正交随机序列的正交化)，且$L(ϵ(1),\cdot \cdot \cdot ,ϵ(k))=L(y(1),\cdot \cdot \cdot ,y(k))$。

【定理】递推射影公式
$$proj(x|y(1),\cdots ,y(k))=proj(x|y(1),\cdots ,y(k-1))+E[x{ϵ}^T(k)][Eϵ(k){ϵ}^T(k){]}^{-1}ϵ(k)\text{\hspace{1em}(1.8)}$$

2. 卡尔曼滤波器

设动态系统模型如下
$$x(t+1)=\Phi x(t)+\Gamma w(t)\text{\hspace{1em}(2.1)}$$

$$y(t)=Hx(t)+v(t)\text{\hspace{1em}(2.2)}$$

假设 $w(t)$ 和 $v(t)$ 满足如下约束条件
$$Ew(t)=0,Ev(t)=0\text{\hspace{1em}(2.3)}$$

$$E[w(i)w^T(j)]=Q{\delta }_{ij},E[v(i)v^T(j)]=R{\delta }_{ij}\text{\hspace{1em}(2.4)}$$

$$E[w(i)v^T(j)]=0,\forall i,j\text{\hspace{1em}(2.5)}$$

其中 ${\delta }_{ii}=1,{\delta }_{ij}=0(i̸=j)$。

下面应用射影定理推导卡尔曼滤波器，在性能指标 $(1.2)$ 下，问题归结为求射影
$$\hat{x}(j|t)=proj(x(j)|y(1),\cdots ,y(t))$$
由递推射影公式 $(1.8)$ 可得
$$\hat{x}(t+1|t+1)=\hat{x}(t+1|t)+K(t+1)ϵ(t+1)$$
对 $(2.1)$ 两边取射影有
$$\hat{x}(t+1|t)=\Phi \hat{x}(t|t)+\Gamma proj(w(t)|y(1),\cdots ,y(t))\text{\hspace{1em}(2.6)}$$
根据系统方程递归展开可知
$$\begin{gathered} x(t)\in L(w(t-1),\cdots ,w(0),x(0)) \\ y(t)\in L(v(t),w(t-1),\cdots ,w(0),x(0)) \end{gathered}$$
由此可知
$$L(y(1),\cdots ,y(t))\subset L(v(t),\cdots ,v(1),w(t-1),\cdots ,w(0),x(0))$$
由于 $x(0),w(t),v(t)$ 互不相关，所以 $w(t)\perp L(y(1),\cdots ,y(t))$ ，所以$proj(w(t)|y(1),\cdots ,y(t))=0$ 。所以式 $(2.6)$ 简化为
$$\hat{x}(t+1|t)=\Phi \hat{x}(t|t)$$
对 $(2.2)$ 两边取射影有
$$\hat{y}(t+1|t)=H\hat{x}(t+1|t)+proj(v(t+1)|y(1),\cdots ,y(t))$$
同理可得 $proj(v(t+1)|y(1),\cdots ,y(t))=0$ 。于是有
$$\hat{y}(t+1|t)=H\hat{x}(t+1|t)$$
引出新息表达式
$$ϵ(t+1)=y(t+1)-\hat{y}(t+1|t)=y(t+1)-H\hat{x}(t+1|t)$$
记误差方差阵为
$$\begin{gathered} \overline{x}(t|t)=x(t)-\hat{x}(t|t) \\ \overline{x}(t+1|t)=x(t+1)-\hat{x}(t+1|t) \\ P(t|t)=E[\overline{x}(t|t){\overline{x}}^T(t|t)] \\ P(t+1|t)=E[\overline{x}(t+1|t){\overline{x}}^T(t+1|t)] \end{gathered}$$
由此，新息可变换为
$$ϵ(t+1)=H\overline{x}(t+1|t)+v(t+1)$$
又有
$$\begin{gathered} \overline{x}(t+1|t)=\Phi \overline{x}(t|t)+\Gamma w(t) \\ \overline{x}(t+1|t+1)=\overline{x}(t+1|t)-K(t+1)ϵ(t+1) \\ =\overline{x}(t+1|t)-K(t+1)\ast (H\overline{x}(t+1|t)+v(t+1)) \\ =[I_n-K(t+1)H]\overline{x}(t+1|t)-K(t+1)v(t+1)\text{\hspace{1em}(2.7)} \end{gathered}$$
由于$\overline{x}(t|t)=x(t)-\hat{x}(t|t)\in L(v(t),\cdots ,v(1),w(t-1),\cdots ,w(0),x(0))$，故有$w(t)\perp \overline{x}(t|t)$，由此可得$E[w(t){\overline{x}}^T(t|t)]=0$。于是，由误差方差阵最后一个方程可得
$$P(t+1|t)=\Phi P(t|t){\Phi }^T+\Gamma Q{\Gamma }^T$$
同理，由$v(t+1)\perp \overline{x}(t+1|t)$ 引出 $E[v(t+1){\overline{x}}^T(t+1|t)]$ ，可得新息误差方差阵为
$$E[ϵ(t+1){ϵ}^T(t+1)]=HP(t+1|t)H^T+R$$
由方程式 $(2.7)$ 可得
$$P(t+1|t+1)=[I_n-K(t+1)H]P(t+1|t)[I_n-K(t+1)H{]}^T+K(t+1)R{K}^T(t+1)$$
易知 $K(t+1)=E[x(t+1){ϵ}^T(t+1)][ϵ(t+1){ϵ}^T(t+1){]}^{-1}$ ，其中
$$E[x(t+1){ϵ}^T(t+1)]=E[(\hat{x}(t+1|t)+\overline{x}(t+1|t))(H\overline{x}(t+1|t)+v(t+1){)}^T]$$
又有 $\hat{x}(t+1|t)\perp \overline{x}(t+1|t),v(t+1)\perp \hat{x}(t+1|t),v(t+1)\perp \overline{x}(t+1|t)$ ，可得
$$K(t+1)=P(t+1|t)H^T[HP(t+1|t)H^T+R{]}^{-1}$$
则可利用 $K(t+1)$ 来简化 $P(t+1|t+1)$ ，即
$$P(t+1|t+1)=[I_n-K(t+1)H]P(t+1|t)$$
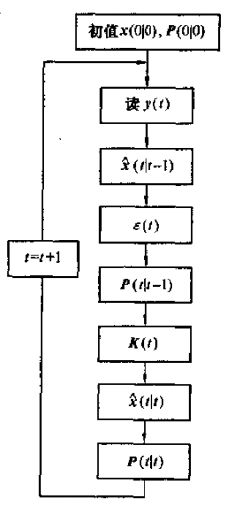
上述推导结果可概括为如下递推卡尔曼滤波器
$$\begin{gathered} \hat{x}(t+1|t+1)=\hat{x}(t+1|t)-K(t+1)ϵ(t+1) \\ \hat{x}(t+1|t)=\Phi \hat{x}(t|t) \\ ϵ(t+1)=y(t+1)-H\hat{x}(t+1|t) \\ K(t+1)=P(t+1|t)H^T[HP(t+1|t)H^T+R{]}^{-1} \\ P(t+1|t)=\Phi P(t|t){\Phi }^T+\Gamma Q{\Gamma }^T \\ P(t+1|t+1)=[I_n-K(t+1)H]P(t+1|t) \\ \hat{x}(0|0)={\mu }_0,P(0|0)=P_0 \end{gathered}$$
卡尔曼滤波算法递推流程图

【定理】当动态系统模型带有控制输入 $u(t)$ 时
$$\begin{gathered} x(t+1)=\Phi x(t)+B(t)u(t)+\Gamma w(t) \\ y(t)=H(t)x(t)+v(t) \end{gathered}$$
此时的卡尔曼滤波器为
$$\begin{gathered} \hat{x}(t+1|t)=\Phi \hat{x}(t|t)+B(t)u(t) \\ ϵ(t+1)=y(t+1)-H\hat{x}(t+1|t) \\ P(t+1|t)=\Phi P(t|t){\Phi }^T+\Gamma Q{\Gamma }^T \\ K(t+1)=P(t+1|t)H^T[HP(t+1|t)H^T+R{]}^{-1} \\ \hat{x}(t+1|t+1)=\hat{x}(t+1|t)+K(t+1)ϵ(t+1) \\ P(t+1|t+1)=[I_n-K(t+1)H]P(t+1|t) \\ \hat{x}(0|0)={\mu }_0,P(0|0)=P_0 \end{gathered}$$

3.扩展卡尔曼滤波器

系统方程如下
$$\begin{gathered} x_t=g(u_t,x_{t-1})+{ϵ}_t \\ {z}_t=h(x_t)+{\delta }_t \end{gathered}$$
算法如下
$$\begin{gathered} {\overline{\mu }}_t=g(u_t,{\mu }_{t-1}) \\ \widehat{\sum _t}=G_t\widehat{\sum _{t-1}}{G}_t^T+R_t \\ {K}_t=\widehat{\sum _t}{H}_t^T(H_t\widehat{\sum _t}{H}_t^T+Q_t{)}^{-1} \\ {\mu }_t={\overline{\mu }}_t+K_t(z_t-h({\overline{\mu }}_t)) \\ \sum _t=(I-K_t{H}_t)\widehat{\sum _t} \end{gathered}$$
其中

	KF	EKF
状态预测	$A_t{\mu }_{t-1}+B_t{u}_t$	$g(u_t,{\mu }_{t-1})$
测量预测	$C{\overline{\mu }}_t$	$h({\overline{\mu }}_t)$
最有估计	$\hat{x}(t\Vert t)$	${\mu }_t$
状态预测	$\hat{x}(t+1\Vert t)$	${\overline{\mu }}_{t+1}$

参考文献

[1] 邓自立. 最优估计理论及其应用[M]. 哈尔滨工业大学出版社, 2005.

[2] Thrun S. Probabilistic robotics[M]. MIT Press, 2006:52-57.

公众号