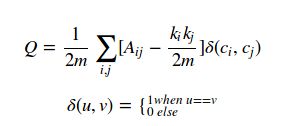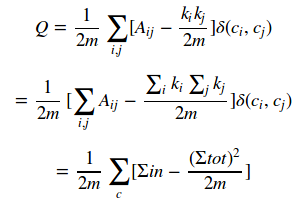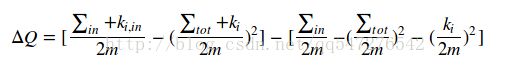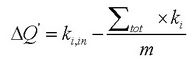Louvain 社团发现算法学习(我的java实现+数据用例)
为了大家方便,直接把数据放在github了:
https://github.com/qq547276542/Louvain
算法介绍:
Louvain 算法是基于模块度的社区发现算法,该算法在效率和效果上都表现较好,并且能够发现层次性的社区结构,其优化目标是最大化整个社区网络的模块度。
社区网络的模块度(Modularity)是评估一个社区网络划分好坏的度量方法,它的含义是社区内节点的连边数与随机情况下的边数之差,它的取值范围是 (0,1),其定义如下:
上式中,Aij代表结点i和j之间的边权值(当图不带权时,边权值可以看成1)。 ki代表结点i的領街边的边权和(当图不带权时,即为结点的度数)。
m为图中所有边的边权和。 ci为结点i所在的社团编号。
模块度的公式定义可以做如下的简化:
其中Sigma in表示社区c内的边的权重之和,Sigma tot表示与社区c内的节点相连的边的权重之和。
我们的目标,是要找出各个结点处于哪一个社团,并且让这个划分结构的模块度最大。
Louvain算法的思想很简单:
1)将图中的每个节点看成一个独立的社区,次数社区的数目与节点个数相同;
2)对每个节点i,依次尝试把节点i分配到其每个邻居节点所在的社区,计算分配前与分配后的模块度变化Delta Q,并记录Delta Q最大的那个邻居节点,如果maxDelta Q>0,则把节点i分配Delta Q最大的那个邻居节点所在的社区,否则保持不变;
3)重复2),直到所有节点的所属社区不再变化;
4)对图进行压缩,将所有在同一个社区的节点压缩成一个新节点,社区内节点之间的边的权重转化为新节点的环的权重,社区间的边权重转化为新节点间的边权重;
5)重复1)直到整个图的模块度不再发生变化。
在写代码时,要注意几个要点:
* 第二步,尝试分配结点时,并不是只尝试独立的结点,也可以尝试所在社区的结点数大于1的点,我在看paper时一开始把这个部分看错了,导致算法出问题。
* 第三步,重复2)的时候,并不是将每个点遍历一次后就对图进行一次重构,而是要不断循环的遍历每个结点,直到一次循环中所有结点所在社区都不更新了,表示当前网络已经稳定,然后才进行图的重构。
* 模块度增益的计算,请继续看下文
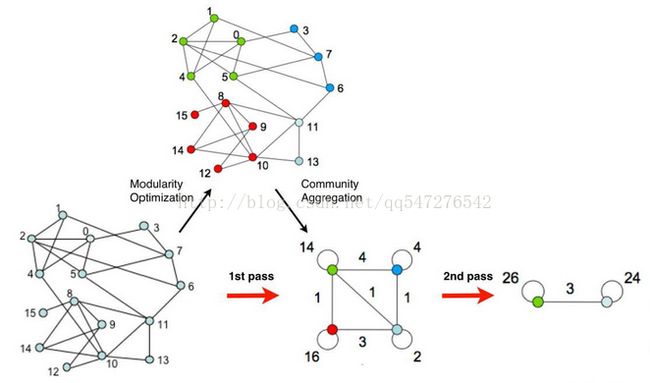
过程如下图所示:
可以看出,louvain是一个启发式的贪心算法。我们需要对模块度进行一个启发式的更新。这样的话这个算法会有如下几个问题:
1:尝试将节点i分配到相邻社团时,如果真的移动结点i,重新计算模块度,那么算法的效率很难得到保证
2:在本问题中,贪心算法只能保证局部最优,而不能够保证全局最优
3:将节点i尝试分配至相邻社团时,要依据一个什么样的顺序
......
第一个问题,在该算法的paper中给了我们解答。我们实际上不用真的把节点i加入相邻社团后重新计算模块度,paper中给了我们一个计算把结点i移动至社团c时,模块度的增益公式:
其中Sigma in表示起点终点都在社区c内的边的权重之和,Sigma tot表示入射社区c内的边的权重之和,ki代表结点i的带权度数和,m为所有边权和。
但是该增益公式还是过于复杂,仍然会影响算法的时间效率。
但是请注意,我们只是想通过模块增益度来判断一个结点i是否能移动到社团c中,而我们实际上是没有必要真正的去求精确的模块度,只需要知道,当前的这步操作,模块度是否发生了增长。
因此,就有了相对增益公式的出现:
相对增益的值可能大于1,不是真正的模块度增长值,但是它的正负表示了当前的操作是否增加了模块度。用该公式能大大降低算法的时间复杂度。
第二个问题,该算法的确不能够保证全局最优。但是我们该算法的启发式规则很合理,因此我们能够得到一个十分精确的近似结果。
同时,为了校准结果,我们可以以不同的序列多次调用该算法,保留一个模块度最大的最优结果。
第三个问题,在第二个问题中也出现了,就是给某个结点i找寻領接点时,应当以一个什么顺序?递增or随机or其它规则?我想这个问题需要用实验数据去分析。
在paper中也有提到一些能够使结果更精确的序列。我的思路是,如果要尝试多次取其最优,取随机序列应该是比较稳定比较精确的方式。
说了这么多,下面给上本人的Louvain算法java实现供参考。 本人代码注释比较多,适合学习。
我的代码后面是国外大牛的代码,时空复杂度和我的代码一样,但是常数比我小很多,速度要快很多,而且答案更精准(迭代了10次),适合实际运用~
本人的java代码:(时间复杂度o(e),空间复杂度o(e))
Edge.java:
package myLouvain;
public class Edge implements Cloneable{
int v; //v表示连接点的编号,w表示此边的权值
double weight;
int next; //next负责连接和此点相关的边
Edge(){}
public Object clone(){
Edge temp=null;
try{
temp = (Edge)super.clone(); //浅复制
}catch(CloneNotSupportedException e) {
e.printStackTrace();
}
return temp;
}
}
Louvain.java:
package myLouvain;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileInputStream;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Random;
public class Louvain implements Cloneable{
int n; // 结点个数
int m; // 边数
int cluster[]; // 结点i属于哪个簇
Edge edge[]; // 邻接表
int head[]; // 头结点下标
int top; // 已用E的个数
double resolution; // 1/2m 全局不变
double node_weight[]; // 结点的权值
double totalEdgeWeight; // 总边权值
double[] cluster_weight; // 簇的权值
double eps = 1e-14; // 误差
int global_n; // 最初始的n
int global_cluster[]; // 最后的结果,i属于哪个簇
Edge[] new_edge; //新的邻接表
int[] new_head;
int new_top = 0;
final int iteration_time = 3; // 最大迭代次数
Edge global_edge[]; //全局初始的临接表 只保存一次,永久不变,不参与后期运算
int global_head[];
int global_top=0;
void addEdge(int u, int v, double weight) {
if(edge[top]==null)
edge[top]=new Edge();
edge[top].v = v;
edge[top].weight = weight;
edge[top].next = head[u];
head[u] = top++;
}
void addNewEdge(int u, int v, double weight) {
if(new_edge[new_top]==null)
new_edge[new_top]=new Edge();
new_edge[new_top].v = v;
new_edge[new_top].weight = weight;
new_edge[new_top].next = new_head[u];
new_head[u] = new_top++;
}
void addGlobalEdge(int u, int v, double weight) {
if(global_edge[global_top]==null)
global_edge[global_top]=new Edge();
global_edge[global_top].v = v;
global_edge[global_top].weight = weight;
global_edge[global_top].next = global_head[u];
global_head[u] = global_top++;
}
void init(String filePath) {
try {
String encoding = "UTF-8";
File file = new File(filePath);
if (file.isFile() && file.exists()) { // 判断文件是否存在
InputStreamReader read = new InputStreamReader(new FileInputStream(file), encoding);// 考虑到编码格式
BufferedReader bufferedReader = new BufferedReader(read);
String lineTxt = null;
lineTxt = bufferedReader.readLine();
////// 预处理部分
String cur2[] = lineTxt.split(" ");
global_n = n = Integer.parseInt(cur2[0]);
m = Integer.parseInt(cur2[1]);
m *= 2;
edge = new Edge[m];
head = new int[n];
for (int i = 0; i < n; i++)
head[i] = -1;
top = 0;
global_edge=new Edge[m];
global_head = new int[n];
for(int i=0;i 2) {
curw = Double.parseDouble(cur[2]);
} else {
curw = 1.0;
}
addEdge(u, v, curw);
addEdge(v, u, curw);
addGlobalEdge(u,v,curw);
addGlobalEdge(v,u,curw);
totalEdgeWeight += 2 * curw;
node_weight[u] += curw;
if (u != v) {
node_weight[v] += curw;
}
}
resolution = 1 / totalEdgeWeight;
read.close();
} else {
System.out.println("找不到指定的文件");
}
} catch (Exception e) {
System.out.println("读取文件内容出错");
e.printStackTrace();
}
}
void init_cluster() {
cluster = new int[n];
for (int i = 0; i < n; i++) { // 一个结点一个簇
cluster[i] = i;
}
}
boolean try_move_i(int i) { // 尝试将i加入某个簇
double[] edgeWeightPerCluster = new double[n];
for (int j = head[i]; j != -1; j = edge[j].next) {
int l = cluster[edge[j].v]; // l是nodeid所在簇的编号
edgeWeightPerCluster[l] += edge[j].weight;
}
int bestCluster = -1; // 最优的簇号下标(先默认是自己)
double maxx_deltaQ = 0.0; // 增量的最大值
boolean[] vis = new boolean[n];
cluster_weight[cluster[i]] -= node_weight[i];
for (int j = head[i]; j != -1; j = edge[j].next) {
int l = cluster[edge[j].v]; // l代表領接点的簇号
if (vis[l]) // 一个領接簇只判断一次
continue;
vis[l] = true;
double cur_deltaQ = edgeWeightPerCluster[l];
cur_deltaQ -= node_weight[i] * cluster_weight[l] * resolution;
if (cur_deltaQ > maxx_deltaQ) {
bestCluster = l;
maxx_deltaQ = cur_deltaQ;
}
edgeWeightPerCluster[l] = 0;
}
if (maxx_deltaQ < eps) {
bestCluster = cluster[i];
}
//System.out.println(maxx_deltaQ);
cluster_weight[bestCluster] += node_weight[i];
if (bestCluster != cluster[i]) { // i成功移动了
cluster[i] = bestCluster;
return true;
}
return false;
}
void rebuildGraph() { // 重构图
/// 先对簇进行离散化
int[] change = new int[n];
int change_size=0;
boolean vis[] = new boolean[n];
for (int i = 0; i < n; i++) {
if (vis[cluster[i]])
continue;
vis[cluster[i]] = true;
change[change_size++]=cluster[i];
}
int[] index = new int[n]; // index[i]代表 i号簇在新图中的结点编号
for (int i = 0; i < change_size; i++)
index[change[i]] = i;
int new_n = change_size; // 新图的大小
new_edge = new Edge[m];
new_head = new int[new_n];
new_top = 0;
double new_node_weight[] = new double[new_n]; // 新点权和
for(int i=0;i[] nodeInCluster = new ArrayList[new_n]; // 代表每个簇中的节点列表
for (int i = 0; i < new_n; i++)
nodeInCluster[i] = new ArrayList();
for (int i = 0; i < n; i++) {
nodeInCluster[index[cluster[i]]].add(i);
}
for (int u = 0; u < new_n; u++) { // 将同一个簇的挨在一起分析。可以将visindex数组降到一维
boolean visindex[] = new boolean[new_n]; // visindex[v]代表新图中u节点到v的边在临街表是第几个(多了1,为了初始化方便)
double delta_w[] = new double[new_n]; // 边权的增量
for (int i = 0; i < nodeInCluster[u].size(); i++) {
int t = nodeInCluster[u].get(i);
for (int k = head[t]; k != -1; k = edge[k].next) {
int j = edge[k].v;
int v = index[cluster[j]];
if (u != v) {
if (!visindex[v]) {
addNewEdge(u, v, 0);
visindex[v] = true;
}
delta_w[v] += edge[k].weight;
}
}
new_node_weight[u] += node_weight[t];
}
for (int k = new_head[u]; k != -1; k = new_edge[k].next) {
int v = new_edge[k].v;
new_edge[k].weight = delta_w[v];
}
}
// 更新答案
int[] new_global_cluster = new int[global_n];
for (int i = 0; i < global_n; i++) {
new_global_cluster[i] = index[cluster[global_cluster[i]]];
}
for (int i = 0; i < global_n; i++) {
global_cluster[i] = new_global_cluster[i];
}
top = new_top;
for (int i = 0; i < m; i++) {
edge[i] = new_edge[i];
}
for (int i = 0; i < new_n; i++) {
node_weight[i] = new_node_weight[i];
head[i] = new_head[i];
}
n = new_n;
init_cluster();
}
void print() {
for (int i = 0; i < global_n; i++) {
System.out.println(i + ": " + global_cluster[i]);
}
System.out.println("-------");
}
void louvain() {
init_cluster();
int count = 0; // 迭代次数
boolean update_flag; // 标记是否发生过更新
do { // 第一重循环,每次循环rebuild一次图
// print(); // 打印簇列表
count++;
cluster_weight = new double[n];
for (int j = 0; j < n; j++) { // 生成簇的权值
cluster_weight[cluster[j]] += node_weight[j];
}
int[] order = new int[n]; // 生成随机序列
for (int i = 0; i < n; i++)
order[i] = i;
Random random = new Random();
for (int i = 0; i < n; i++) {
int j = random.nextInt(n);
int temp = order[i];
order[i] = order[j];
order[j] = temp;
}
int enum_time = 0; // 枚举次数,到n时代表所有点已经遍历过且无移动的点
int point = 0; // 循环指针
update_flag = false; // 是否发生过更新的标记
do {
int i = order[point];
point = (point + 1) % n;
if (try_move_i(i)) { // 对i点做尝试
enum_time = 0;
update_flag = true;
} else {
enum_time++;
}
} while (enum_time < n);
if (count > iteration_time || !update_flag) // 如果没更新过或者迭代次数超过指定值
break;
rebuildGraph(); // 重构图
} while (true);
}
}
Main.java:
package myLouvain;
import java.io.BufferedWriter;
import java.io.FileWriter;
import java.io.IOException;
import java.util.ArrayList;
public class Main {
public static void writeOutputJson(String fileName, Louvain a) throws IOException {
BufferedWriter bufferedWriter;
bufferedWriter = new BufferedWriter(new FileWriter(fileName));
bufferedWriter.write("{\n\"nodes\": [\n");
for(int i=0;i();
}
for(int i=0;i 用d3绘图工具对上文那张16个结点的图的划分进行louvain算法后的可视化结果:
对一个4000个结点,80000条边的无向图(facebook数据)运行我的louvain算法,大概需要1秒多的时间,划分的效果还可以,可视化效果(边有点多了,都粘在一块了):
//////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
下面是国外大牛的代码实现(为了大家方便直接贴上了,时间复杂度o(e),空间复杂度o(e)):
ModularityOptimizer.javaimport java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.FileReader;
import java.io.FileWriter;
import java.io.IOException;
import java.util.Arrays;
import java.util.Random;
public class ModularityOptimizer
{
public static void main(String[] args) throws IOException
{
boolean update;
double modularity, maxModularity, resolution, resolution2;
int algorithm, i, j, modularityFunction, nClusters, nIterations, nRandomStarts;
int[] cluster;
double beginTime, endTime;
Network network;
Random random;
String inputFileName, outputFileName;
inputFileName = "/home/eason/Louvain/facebook_combined.txt";
outputFileName = "/home/eason/Louvain/answer.txt";
modularityFunction = 1;
resolution = 1.0;
algorithm = 1;
nRandomStarts = 10;
nIterations = 3;
System.out.println("Modularity Optimizer version 1.2.0 by Ludo Waltman and Nees Jan van Eck");
System.out.println();
System.out.println("Reading input file...");
System.out.println();
network = readInputFile(inputFileName, modularityFunction);
System.out.format("Number of nodes: %d%n", network.getNNodes());
System.out.format("Number of edges: %d%n", network.getNEdges() / 2);
System.out.println();
System.out.println("Running " + ((algorithm == 1) ? "Louvain algorithm" : ((algorithm == 2) ? "Louvain algorithm with multilevel refinement" : "smart local moving algorithm")) + "...");
System.out.println();
resolution2 = ((modularityFunction == 1) ? (resolution / network.getTotalEdgeWeight()) : resolution);
beginTime = System.currentTimeMillis();
cluster = null;
nClusters = -1;
maxModularity = Double.NEGATIVE_INFINITY;
random = new Random(100);
for (i = 0; i < nRandomStarts; i++)
{
if (nRandomStarts > 1)
System.out.format("Random start: %d%n", i + 1);
network.initSingletonClusters(); //网络初始化,每个节点一个簇
j = 0;
update = true;
do
{
if (nIterations > 1)
System.out.format("Iteration: %d%n", j + 1);
if (algorithm == 1)
update = network.runLouvainAlgorithm(resolution2, random);
j++;
modularity = network.calcQualityFunction(resolution2);
if (nIterations > 1)
System.out.format("Modularity: %.4f%n", modularity);
}
while ((j < nIterations) && update);
if (modularity > maxModularity) {
cluster = network.getClusters();
nClusters = network.getNClusters();
maxModularity = modularity;
}
if (nRandomStarts > 1)
{
if (nIterations == 1)
System.out.format("Modularity: %.8f%n", modularity);
System.out.println();
}
}
endTime = System.currentTimeMillis();
if (nRandomStarts == 1)
{
if (nIterations > 1)
System.out.println();
System.out.format("Modularity: %.8f%n", maxModularity);
}
else
System.out.format("Maximum modularity in %d random starts: %f%n", nRandomStarts, maxModularity);
System.out.format("Number of communities: %d%n", nClusters);
System.out.format("Elapsed time: %.4f seconds%n", (endTime - beginTime) / 1000.0);
System.out.println();
System.out.println("Writing output file...");
System.out.println();
writeOutputFile(outputFileName, cluster);
}
private static Network readInputFile(String fileName, int modularityFunction) throws IOException
{
BufferedReader bufferedReader;
double[] edgeWeight1, edgeWeight2, nodeWeight;
int i, j, nEdges, nLines, nNodes;
int[] firstNeighborIndex, neighbor, nNeighbors, node1, node2;
Network network;
String[] splittedLine;
bufferedReader = new BufferedReader(new FileReader(fileName));
nLines = 0;
while (bufferedReader.readLine() != null)
nLines++;
bufferedReader.close();
bufferedReader = new BufferedReader(new FileReader(fileName));
node1 = new int[nLines];
node2 = new int[nLines];
edgeWeight1 = new double[nLines];
i = -1;
bufferedReader.readLine() ;
for (j = 1; j < nLines; j++)
{
splittedLine = bufferedReader.readLine().split(" ");
node1[j] = Integer.parseInt(splittedLine[0]);
if (node1[j] > i)
i = node1[j];
node2[j] = Integer.parseInt(splittedLine[1]);
if (node2[j] > i)
i = node2[j];
edgeWeight1[j] = (splittedLine.length > 2) ? Double.parseDouble(splittedLine[2]) : 1;
}
nNodes = i + 1;
bufferedReader.close();
nNeighbors = new int[nNodes];
for (i = 0; i < nLines; i++)
if (node1[i] < node2[i])
{
nNeighbors[node1[i]]++;
nNeighbors[node2[i]]++;
}
firstNeighborIndex = new int[nNodes + 1];
nEdges = 0;
for (i = 0; i < nNodes; i++)
{
firstNeighborIndex[i] = nEdges;
nEdges += nNeighbors[i];
}
firstNeighborIndex[nNodes] = nEdges;
neighbor = new int[nEdges];
edgeWeight2 = new double[nEdges];
Arrays.fill(nNeighbors, 0);
for (i = 0; i < nLines; i++)
if (node1[i] < node2[i])
{
j = firstNeighborIndex[node1[i]] + nNeighbors[node1[i]];
neighbor[j] = node2[i];
edgeWeight2[j] = edgeWeight1[i];
nNeighbors[node1[i]]++;
j = firstNeighborIndex[node2[i]] + nNeighbors[node2[i]];
neighbor[j] = node1[i];
edgeWeight2[j] = edgeWeight1[i];
nNeighbors[node2[i]]++;
}
{
nodeWeight = new double[nNodes];
for (i = 0; i < nEdges; i++)
nodeWeight[neighbor[i]] += edgeWeight2[i];
network = new Network(nNodes, firstNeighborIndex, neighbor, edgeWeight2, nodeWeight);
}
return network;
}
private static void writeOutputFile(String fileName, int[] cluster) throws IOException
{
BufferedWriter bufferedWriter;
int i;
bufferedWriter = new BufferedWriter(new FileWriter(fileName));
for (i = 0; i < cluster.length; i++)
{
bufferedWriter.write(Integer.toString(cluster[i]));
bufferedWriter.newLine();
}
bufferedWriter.close();
}
} Network.java
import java.io.Serializable;
import java.util.Random;
public class Network implements Cloneable, Serializable {
private static final long serialVersionUID = 1;
private int nNodes;
private int[] firstNeighborIndex;
private int[] neighbor;
private double[] edgeWeight;
private double[] nodeWeight;
private int nClusters;
private int[] cluster;
private double[] clusterWeight;
private int[] nNodesPerCluster;
private int[][] nodePerCluster;
private boolean clusteringStatsAvailable;
public Network(int nNodes, int[] firstNeighborIndex, int[] neighbor, double[] edgeWeight, double[] nodeWeight) {
this(nNodes, firstNeighborIndex, neighbor, edgeWeight, nodeWeight, null);
}
public Network(int nNodes, int[] firstNeighborIndex, int[] neighbor, double[] edgeWeight, double[] nodeWeight,
int[] cluster) {
int i, nEdges;
this.nNodes = nNodes;
this.firstNeighborIndex = firstNeighborIndex;
this.neighbor = neighbor;
if (edgeWeight == null) {
nEdges = neighbor.length;
this.edgeWeight = new double[nEdges];
for (i = 0; i < nEdges; i++)
this.edgeWeight[i] = 1;
} else
this.edgeWeight = edgeWeight;
if (nodeWeight == null) {
this.nodeWeight = new double[nNodes];
for (i = 0; i < nNodes; i++)
this.nodeWeight[i] = 1;
} else
this.nodeWeight = nodeWeight;
}
public int getNNodes() {
return nNodes;
}
public int getNEdges() {
return neighbor.length;
}
public double getTotalEdgeWeight() // 计算总边权
{
double totalEdgeWeight;
int i;
totalEdgeWeight = 0;
for (i = 0; i < neighbor.length; i++)
totalEdgeWeight += edgeWeight[i];
return totalEdgeWeight;
}
public double[] getEdgeWeights() {
return edgeWeight;
}
public double[] getNodeWeights() {
return nodeWeight;
}
public int getNClusters() {
return nClusters;
}
public int[] getClusters() {
return cluster;
}
public void initSingletonClusters() {
int i;
nClusters = nNodes;
cluster = new int[nNodes];
for (i = 0; i < nNodes; i++)
cluster[i] = i;
deleteClusteringStats();
}
public void mergeClusters(int[] newCluster) {
int i, j, k;
if (cluster == null)
return;
i = 0;
for (j = 0; j < nNodes; j++) {
k = newCluster[cluster[j]];
if (k > i)
i = k;
cluster[j] = k;
}
nClusters = i + 1;
deleteClusteringStats();
}
public Network getReducedNetwork() {
double[] reducedNetworkEdgeWeight1, reducedNetworkEdgeWeight2;
int i, j, k, l, m, reducedNetworkNEdges1, reducedNetworkNEdges2;
int[] reducedNetworkNeighbor1, reducedNetworkNeighbor2;
Network reducedNetwork;
if (cluster == null)
return null;
if (!clusteringStatsAvailable)
calcClusteringStats();
reducedNetwork = new Network();
reducedNetwork.nNodes = nClusters;
reducedNetwork.firstNeighborIndex = new int[nClusters + 1];
reducedNetwork.nodeWeight = new double[nClusters];
reducedNetworkNeighbor1 = new int[neighbor.length];
reducedNetworkEdgeWeight1 = new double[edgeWeight.length];
reducedNetworkNeighbor2 = new int[nClusters - 1];
reducedNetworkEdgeWeight2 = new double[nClusters];
reducedNetworkNEdges1 = 0;
for (i = 0; i < nClusters; i++) {
reducedNetworkNEdges2 = 0;
for (j = 0; j < nodePerCluster[i].length; j++) {
k = nodePerCluster[i][j]; // k是簇i中第j个节点的id
for (l = firstNeighborIndex[k]; l < firstNeighborIndex[k + 1]; l++) {
m = cluster[neighbor[l]]; // m是k的在l位置的邻居节点所属的簇id
if (m != i) {
if (reducedNetworkEdgeWeight2[m] == 0) {
reducedNetworkNeighbor2[reducedNetworkNEdges2] = m;
reducedNetworkNEdges2++;
}
reducedNetworkEdgeWeight2[m] += edgeWeight[l];
}
}
reducedNetwork.nodeWeight[i] += nodeWeight[k];
}
for (j = 0; j < reducedNetworkNEdges2; j++) {
reducedNetworkNeighbor1[reducedNetworkNEdges1 + j] = reducedNetworkNeighbor2[j];
reducedNetworkEdgeWeight1[reducedNetworkNEdges1
+ j] = reducedNetworkEdgeWeight2[reducedNetworkNeighbor2[j]];
reducedNetworkEdgeWeight2[reducedNetworkNeighbor2[j]] = 0;
}
reducedNetworkNEdges1 += reducedNetworkNEdges2;
reducedNetwork.firstNeighborIndex[i + 1] = reducedNetworkNEdges1;
}
reducedNetwork.neighbor = new int[reducedNetworkNEdges1];
reducedNetwork.edgeWeight = new double[reducedNetworkNEdges1];
System.arraycopy(reducedNetworkNeighbor1, 0, reducedNetwork.neighbor, 0, reducedNetworkNEdges1);
System.arraycopy(reducedNetworkEdgeWeight1, 0, reducedNetwork.edgeWeight, 0, reducedNetworkNEdges1);
return reducedNetwork;
}
public double calcQualityFunction(double resolution) {
double qualityFunction, totalEdgeWeight;
int i, j, k;
if (cluster == null)
return Double.NaN;
if (!clusteringStatsAvailable)
calcClusteringStats();
qualityFunction = 0;
totalEdgeWeight = 0;
for (i = 0; i < nNodes; i++) {
j = cluster[i];
for (k = firstNeighborIndex[i]; k < firstNeighborIndex[i + 1]; k++) {
if (cluster[neighbor[k]] == j)
qualityFunction += edgeWeight[k];
totalEdgeWeight += edgeWeight[k];
}
}
for (i = 0; i < nClusters; i++)
qualityFunction -= clusterWeight[i] * clusterWeight[i] * resolution;
qualityFunction /= totalEdgeWeight;
return qualityFunction;
}
public boolean runLocalMovingAlgorithm(double resolution) {
return runLocalMovingAlgorithm(resolution, new Random());
}
public boolean runLocalMovingAlgorithm(double resolution, Random random) {
boolean update;
double maxQualityFunction, qualityFunction;
double[] clusterWeight, edgeWeightPerCluster;
int bestCluster, i, j, k, l, nNeighboringClusters, nStableNodes, nUnusedClusters;
int[] neighboringCluster, newCluster, nNodesPerCluster, nodeOrder, unusedCluster;
if ((cluster == null) || (nNodes == 1))
return false;
update = false;
clusterWeight = new double[nNodes];
nNodesPerCluster = new int[nNodes];
for (i = 0; i < nNodes; i++) {
clusterWeight[cluster[i]] += nodeWeight[i];
nNodesPerCluster[cluster[i]]++;
}
nUnusedClusters = 0;
unusedCluster = new int[nNodes];
for (i = 0; i < nNodes; i++)
if (nNodesPerCluster[i] == 0) {
unusedCluster[nUnusedClusters] = i;
nUnusedClusters++;
}
nodeOrder = new int[nNodes];
for (i = 0; i < nNodes; i++)
nodeOrder[i] = i;
for (i = 0; i < nNodes; i++) {
j = random.nextInt(nNodes);
k = nodeOrder[i];
nodeOrder[i] = nodeOrder[j];
nodeOrder[j] = k;
}
edgeWeightPerCluster = new double[nNodes];
neighboringCluster = new int[nNodes - 1];
nStableNodes = 0;
i = 0;
do {
j = nodeOrder[i];
nNeighboringClusters = 0;
for (k = firstNeighborIndex[j]; k < firstNeighborIndex[j + 1]; k++) {
l = cluster[neighbor[k]];
if (edgeWeightPerCluster[l] == 0) {
neighboringCluster[nNeighboringClusters] = l;
nNeighboringClusters++;
}
edgeWeightPerCluster[l] += edgeWeight[k];
}
clusterWeight[cluster[j]] -= nodeWeight[j];
nNodesPerCluster[cluster[j]]--;
if (nNodesPerCluster[cluster[j]] == 0) {
unusedCluster[nUnusedClusters] = cluster[j];
nUnusedClusters++;
}
bestCluster = -1;
maxQualityFunction = 0;
for (k = 0; k < nNeighboringClusters; k++) {
l = neighboringCluster[k];
qualityFunction = edgeWeightPerCluster[l] - nodeWeight[j] * clusterWeight[l] * resolution;
if ((qualityFunction > maxQualityFunction)
|| ((qualityFunction == maxQualityFunction) && (l < bestCluster))) {
bestCluster = l;
maxQualityFunction = qualityFunction;
}
edgeWeightPerCluster[l] = 0;
}
if (maxQualityFunction == 0) {
bestCluster = unusedCluster[nUnusedClusters - 1];
nUnusedClusters--;
}
clusterWeight[bestCluster] += nodeWeight[j];
nNodesPerCluster[bestCluster]++;
if (bestCluster == cluster[j])
nStableNodes++;
else {
cluster[j] = bestCluster;
nStableNodes = 1;
update = true;
}
i = (i < nNodes - 1) ? (i + 1) : 0;
} while (nStableNodes < nNodes); // 优化步骤是直到所有的点都稳定下来才结束
newCluster = new int[nNodes];
nClusters = 0;
for (i = 0; i < nNodes; i++)
if (nNodesPerCluster[i] > 0) {
newCluster[i] = nClusters;
nClusters++;
}
for (i = 0; i < nNodes; i++)
cluster[i] = newCluster[cluster[i]];
deleteClusteringStats();
return update;
}
public boolean runLouvainAlgorithm(double resolution) {
return runLouvainAlgorithm(resolution, new Random());
}
public boolean runLouvainAlgorithm(double resolution, Random random) {
boolean update, update2;
Network reducedNetwork;
if ((cluster == null) || (nNodes == 1))
return false;
update = runLocalMovingAlgorithm(resolution, random);
if (nClusters < nNodes) {
reducedNetwork = getReducedNetwork();
reducedNetwork.initSingletonClusters();
update2 = reducedNetwork.runLouvainAlgorithm(resolution, random);
if (update2) {
update = true;
mergeClusters(reducedNetwork.getClusters());
}
}
deleteClusteringStats();
return update;
}
private Network() {
}
private void calcClusteringStats() {
int i, j;
clusterWeight = new double[nClusters];
nNodesPerCluster = new int[nClusters];
nodePerCluster = new int[nClusters][];
for (i = 0; i < nNodes; i++) {
clusterWeight[cluster[i]] += nodeWeight[i];
nNodesPerCluster[cluster[i]]++;
}
for (i = 0; i < nClusters; i++) {
nodePerCluster[i] = new int[nNodesPerCluster[i]];
nNodesPerCluster[i] = 0;
}
for (i = 0; i < nNodes; i++) {
j = cluster[i];
nodePerCluster[j][nNodesPerCluster[j]] = i;
nNodesPerCluster[j]++;
}
clusteringStatsAvailable = true;
}
private void deleteClusteringStats() {
clusterWeight = null;
nNodesPerCluster = null;
nodePerCluster = null;
clusteringStatsAvailable = false;
}
}最后给上测试数据的链接,里面有facebook,亚马逊等社交信息数据,供大家调试用:
http://snap.stanford.edu/data/#socnets
如果我有写的不对的地方,欢迎指正,相互学习!