图的广度优先遍历和最短路径算法

目录

 

         图的广度优先遍历和最短路径算法

前言

广度优先遍历算法的探讨

核心代码分析

测试用例

完整代码获取

博客文章版权声明

---

                    图的广度优先遍历和最短路径算法

前言

---

上一次，我们讨论了有关图的深度优先遍历算法，既然二叉树有深度遍历算法，图也有深度遍历算法。那么二叉树还有广度优先遍历算法，图又有没有广度优先算法呢？

答案当然是有的。所谓的广度优先遍历与深度优先遍历的不同就体现在“广度”这个词上，“深度优先”遍历算法讲究的是能遍历到多“深”就遍历到多深，完成了“深”的条件在来考虑“广”的条件。而“广度优先”遍历算法就恰恰相反了，“广度”优先遍历体现在一个“广”字上，即一次将某个节点所有的相邻节点都遍历完了，再去“深”度的往下遍历。

 

广度优先遍历算法的探讨

---

如果看过我前几篇讲“二叉树的广度遍历”的博文就知道，“广度遍历”要使用一个队列来作为辅助工具。如果没看过但感兴趣的同学可以点击此处跳转到这篇讲“二叉树广度优先遍历”的博文。建议先了解一下二叉树的“广度优先遍历”能够更好的理解图的“广度优先遍历算法”。

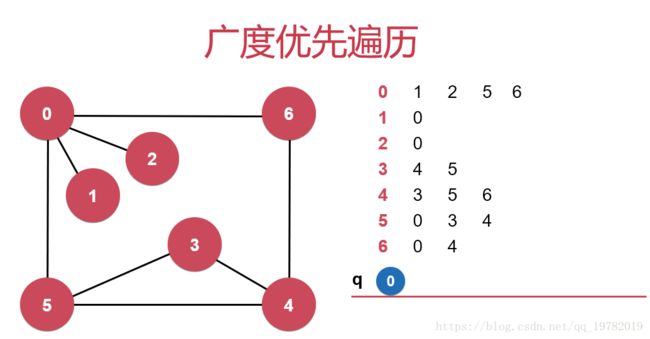
下面我们来探讨一下如何实现图的“广度优先遍历算法”。来看下面这张图：

 

首先，上图左边的是一个简单的无向图，右上方是一个表格，描述了每个节点与之相连的所有邻节点。右下方是一个队列q。还有新增一个ord数组用来计算节点与起始节点之间的距离。首先把起始节点（假设0为起始节点）压入队列中，设置ord[0]=0。标记0节点的visited状态为true，那么此时0节点就已经被遍历了，接下来不能立马让0节点出队列，因为0节点还有一群“跟随”他的邻节点还没入队列呢！所谓的广度优先，就是尽量把节点与之相邻的所有临节点都遍历完再往“深”出去遍历，因此，0节点不仅不能立马出队，还要把他的所有的“邻居节点”都拉进队列里来，他才能安心的离开队列。因为他的邻节点不仅仅是他一个人的邻节点，也有可能是其他节点的邻节点，因此，有可能其他的邻节点已经先把他的部分邻居节点拉入队列中了，所以“拉邻居节点入队列”要排除已经入队列的“邻居节点”，那又如何判断一个节点是否已经进入队列了呢？别忘记了！我们还有一个visited数组记录着呢，任意一个节点只要进入了队列，其visited状态就会置为true。所以，按照这个思路，0节点在出队列之前要把他所有的“邻居节点”中符合条件的节点一起拉入队列中，其中0节点的邻居节点是1,2,5,6，这四个节点的visited状态都为false，所以把他们拉进队伍，并把visited状态置为true，把from[1],from[2],from[5],from[6]都置为0，表示这4个节点都是从0节点遍历过来的。最后，设置ord[1]=ord[0]+1,ord[2]=ord[0]+1,ord[5]=ord[0]+1,ord[6]=ord[0]+1。这样，0节点才完成了他应该完成的所有任务，可以允许出列了！

 

接下来，队列中的首节点是1号节点，轮到1号节点完成任务了，visited[0]=true,但0号节点已经入队过了，所以没有邻居节点可以被1节点拉进队列了，没有新的节点入队，因此此时不用维护from，ord这两个表了，1节点可以允许出列了。

只要队列不为空，那么队列就可以按照上面的规则一直执行下去，直到队列为空，此时图中所有的节点就都已经入队，并完成了相应的数据维护工作，图的“广度优先遍历”就已经完成了。剩余的部分我用下面动画来演示：

广度优先遍历算法动画演示

 

 

核心代码分析

---

广度优先算法的核心类结构：

using namespace std;
template 
class shortPath {
private:
    Graph &G;//接受需要检测的图
    bool *visited;//visited数组用来记录节点是否被访问过
    int s;//s为source的意思。即需要寻路的源（起始）节点
    int *ord;//ord为一个记录各节点到原点之间距离的数组
    int *from;//数组用来记录每个节点的上一个节点编号

核心类的初始化以及广度优先算法的核心实现代码：

public:
    shortPath(Graph &G, int s) : G(G), s(s) {
        assert(s >= 0 && s < G.V());
        //构造辅助数组
        visited = new bool[G.V()];
        ord = new int[G.V()];
        from = new int[G.V()];
        //初始化辅助数组
        for (int i = 0; i < G.V(); i++) {
            visited[i] = false;
            ord[i] = -1;
            from[i] = -1;
        }

        //层序遍历关键代码
        queue q;//准备层序遍历关键工具——辅助队列
        //初始化基础数据
        q.push(s);//源点先入列
        visited[s] = true;//只要入列的节点visited状态就标记为true
        ord[s] = 0;//源点到源点的距离为0
        //利用循环补充剩下的数据
        while (!q.empty()) {
            int v = q.front();//获取队列首元素
            typename Graph::adjIterator adj(G, v);//获取v节点的所有邻节点的迭代器
            //把其所有邻节点中未进入队列等待的节点都加入队列中
            for (int i = adj.begin(); !adj.end(); i = adj.next()) {
                if (!visited[i]) {
                    q.push(i);
                    //下面维护节点关系数据
                    visited[i] = true;//只要成功进入队列的节点就置visited状态为true
                    from[i] = v;//记录前置节点
                    ord[i] = ord[v] + 1;//记录距离
                }
            }
            q.pop();//队列首节点所有工作已经全部完成，可以退出队列了

        }


    }

查询源点到终点之间最短距离的方法实现：

//查询任意一个节点w到源点s之间的最短距离
    int length(int w) {
        assert(w >= 0 && w < G.V());
        return ord[w];
    }

显示路径的方法和前面讲的深度优先算法的实现是一样的：

  //判断两点之间是否有路
    bool hasPath(int w) {//w为寻路终点
        assert(w >= 0 && w < G.V());
        return visited[w];
    }


    //执行寻路算法
    void path(int w, vector &vec) {//传入终点w和一个空的向量vec从来存储路径
        assert(w >= 0 && w < G.V());
        stack stack1;
        while (w != -1) {
            stack1.push(w);//把s到w的路径逆序压入栈中，再从栈中取出来时就是顺序了
            w = from[w];//起始点s的from[s]一直没被重置过，为初始值-1
        }
        vec.clear();
        while (!stack1.empty()) {//从栈中取出路径，此时的路径为顺序
            vec.push_back(stack1.top());//顺序压入向量中
            stack1.pop();
        }

    }

    //显示寻路算法算出来的路径
    void showPath(int w) {
        vector vec;
        path(w, vec);//到此时vec从空向量变成了一个存储着路径序列的向量
        //控制输出格式
        cout << "the route from  " << s << " to " << w << " is :" << endl;
        for (int i = 0; i != vec.size(); i++) {
            if (i == vec.size() - 1) {
                cout << vec[i] << endl;
            } else {
                cout << vec[i] << "->";
            }
        }

    }

 

测试用例

---

测试驱动函数如下：

#include 
#include 
#include 
#include 
#include "SparseGraph.h"
#include "DenseGraph.h"
#include "Path.h"
#include "shortPath.h"
using namespace std;
int main() {
    int N=7;
    int end;
 DenseGraph g2(N, false);//生成一个无向的稠密图用来进行测试
//添加指定的边用作测试
g2.addEdge(0,1);
g2.addEdge(0,2);
g2.addEdge(0,5);
g2.addEdge(0,6);
g2.addEdge(5,3);
g2.addEdge(5,4);
g2.addEdge(3,4);
g2.addEdge(4,6);

shortPath bfs(g2,0);
end=4;
bfs.showPath(end);
cout<<"the length  is:"<

 

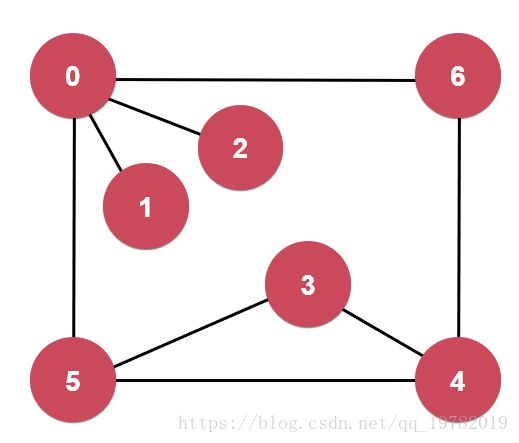
测试用的图结构如下图所示：

测试结果如下：

修改end的值为6,测试结果如下：

 

完整代码获取

---

如需访问完整的工程文件，请点击此处跳转至GitHub。

 

博客文章版权声明

---

第一条 本博客文章仅代表作者本人的观点，不保证文章等内容的有效性。

第二条 本博客部分内容转载于合作站点或摘录于部分书籍，但都会注明作/译者和原出处。如有不妥之处，敬请指出。

第三条 在征得本博客作者同意的情况下，本博客的作品允许非盈利性引用，并请注明出处：“作者：____转载自____”字样，以尊重作者的劳动成果。版权归原作/译者所有。未经允许，严禁转载。

第四条 对非法转载者，“扬俊的小屋”和作/译者保留采用法律手段追究的权利。

第五条 本博客之声明以及其修改权、更新权及最终解释权均属“扬俊的小屋”。

第六条 以上声明的解释权归“扬俊的小屋”所有。