Dv-Hop Algorithm

无需测距的定位技术仿真——Dv-Hop算法
仿真软件——MATLAB

1、定位算法实现
1.1基本原理
DV-Hop 定位算法的原理与经典的距离矢量路由算法比较相似。在DV-Hop算法中，锚节点向网络广播一个信标，信标中包含有此锚节点的位置信息和一个初始值为1的表示跳数的参数。此信标在网络中被以泛洪的方式传播出去，信标每次被转发时跳数都增加1。接收节点在它收到的关于某一个锚节点的所有信标中保存具有最小跳数值的信标，丢弃具有较大跳数值的同一锚节点的信标。通过这一机制，网络中所有节点都获得了到每一个锚节点的最小跳数值。
为了将跳数值转换成物理距离，系统需要估计网络中平均每跳的距离。锚节点具有到网络内部其他锚节点的跳数值以及这些锚节点的位置信息，因此锚节点可以通过计算得到距其他锚节点的实际距离。经过计算，一个锚节点得到网络的平均每跳距离，并将此估计值广播到网络中，称作校正值。任何节点一旦接收到此校正值，且能够获得到3个以上锚节点的估计距离，就可以估计自己到这个锚节点的距离。DV-Hop算法与基于测距算法具有相似之处，就是都需要获得未知节点到锚节点的距离，但是DV-Hop 获得距离的方法是通过网络中拓扑结构信息的计算而不是通过无线电波信号的测量。

1.2 代码实现

% DV-Hop算法
% BorderLength-----正方形区域的边长，单位：m
% NodeAmount-------网络节点的个数
% BeaconAmount---信标节点数
% Sxy--------------用于存储节点的序号，横坐标，纵坐标的矩阵
%Beacon----------信标节点坐标矩阵;BeaconAmount*BeaconAmount
%UN-------------未知节点坐标矩阵;2*UNAmount
% Distance------未知节点到信标节点距离矩阵;2*BeaconAmount
%h---------------节点间初始跳数矩阵
%X---------------节点估计坐标初始矩阵,X=[x,y]'
% R------------------节点的通信距离，一般为10-100m
clear,close all;
BorderLength=100;
NodeAmount=100;
BeaconAmount=8;
UNAmount=NodeAmount-BeaconAmount;
R=50;
% D=zeros(NodeAmount,NodeAmount);%未知节电到信标节点距离初始矩阵；BeaconAmount行NodeAmount列
h=zeros(NodeAmount,NodeAmount);%初始跳数为0；BeaconAmount行NodeAmount列
X=zeros(2,UNAmount);%节点估计坐标初始矩阵
%在正方形区域内产生均匀分布的随机拓扑
C=BorderLength.*rand(2,NodeAmount);
%带逻辑号的节点坐标
Sxy=[[1:NodeAmount];C];
Beacon=[Sxy(2,1:BeaconAmount);Sxy(3,1:BeaconAmount)];%信标节点坐标
UN=[Sxy(2,(BeaconAmount+1):NodeAmount);Sxy(3,(BeaconAmount+1):NodeAmount)];%未知节点坐标
%画出节点分布图
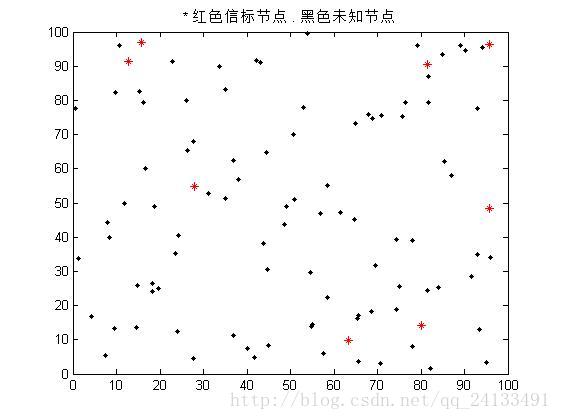
plot(Sxy(2,1:BeaconAmount),Sxy(3,1:BeaconAmount),'r*',Sxy(2,(BeaconAmount+1):NodeAmount),Sxy(3,(BeaconAmount+1):NodeAmount),'k.')
xlim([0,BorderLength]);
ylim([0,BorderLength]);
title('* 红色信标节点 . 黑色未知节点')
%初始化节点间距离、跳数矩阵
for i=1:NodeAmount
    for j=1:NodeAmount
        Dall(i,j)=((Sxy(2,i)-Sxy(2,j))^2+(Sxy(3,i)-Sxy(3,j))^2)^0.5;%所有节点间相互距离
        if (Dall(i,j)<=R)&(Dall(i,j)>0)
            h(i,j)=1;%初始跳数矩阵
        elseif i==j
            h(i,j)=0;
        else h(i,j)=inf;
        end
    end
end
%最短路经算法计算节点间跳数
for k=1:NodeAmount
    for i=1:NodeAmount
        for j=1:NodeAmount
            if h(i,k)+h(k,j)i,j)%min(h(i,j),h(i,k)+h(k,j))
                h(i,j)=h(i,k)+h(k,j);
            end
        end
    end
end
h
%求每个信标节点的校正值
h1=h(1:BeaconAmount,1:BeaconAmount);
D1=Dall(1:BeaconAmount,1:BeaconAmount);
for i=1:BeaconAmount
    dhop(i,1)=sum(D1(i,:))/sum(h1(i,:));%每个信标节点的平均每跳距离
end
D2=Dall(1:BeaconAmount,(BeaconAmount+1):NodeAmount);%BeaconAmount行UNAmount列
for i=1:BeaconAmount
    for j=1:UNAmount
        if min(D2(:,j))==D2(i,j)
            Dhop(1,j)=D2(i,j);%未知节点从最近的信标获得校正值
        end
    end
end
Dhop
%用跳数估计距离
hop1=h(1:BeaconAmount,(BeaconAmount+1):NodeAmount)%未知节点到信标跳数，BeaconAmount行UNAmount列
for i=1:UNAmount
    hop=Dhop(1,i);%hop为从最近信标获得的校正值
    Distance(:,i)=hop*hop1(:,i);%%Beacon行UN列；
end
% %最小二乘法求未知点坐标
d=Distance;
for i=1:2
    for j=1:(BeaconAmount-1)
      a(i,j)=Beacon(i,j)-Beacon(i,BeaconAmount);
    end
end
A=-2*(a');
% d=d1';
 for m=1:UNAmount
     for i=1:(BeaconAmount-1)
         B(i,1)=d(i,m)^2-d(BeaconAmount,m)^2-Beacon(1,i)^2+Beacon(1,BeaconAmount)^2-Beacon(2,i)^2+Beacon(2,BeaconAmount)^2;
     end
           X1=inv(A'*A)*A'*B;
           X(1,m)=X1(1,1);
           X(2,m)=X1(2,1);
 end
 UN
 X
 for i=1:UNAmount
     error(1,i)=(((X(1,i)-UN(1,i))^2+(X(2,i)-UN(2,i))^2)^0.5);
 end
 figure;plot(error,'-o')
 title('每个未知节点的误差')
 error=sum(error)/UNAmount
 Accuracy=error/R

2、仿真结果和分析
2.1 仿真结果

2.2 误差分析
①由于传感器节点随机分布和广播分组过程中可能存在冲突等因素，节点得到的到信标节点的最小跳数存在有一定偏差，且跳数越多，偏差越大。
②在信标节点估算平均每跳距离时，所利用的是除本节点外所有其他信标节点，所以得到的是全网络范围内的平均每跳距离，不能反映本信标节点局部范围内的网络分布情况。
③位置节点在最后阶段估算自身位置时，利用最近的信标节点的平均每跳距离，不能反映出该未知节点局部范围内的网络分布情况。

2.3 结论
虽然DV-Hop算法相对基于测距的定位技术精度较低,但不需要节点具备测距能力,无需额外硬件、能耗较低、受环境影响较小,算法简单,易于实现,对于各向同性的密集网络,可以得到合理的平均每跳距离,定位精度等方面能满足大多数应用的要求,在硬件尺寸和功耗上更适合大规模低能耗的WSN,是目前备受关注的定位机制,许多定位系统都采用了该算法来实现。由于节点是随机部署的,未知节点与信标节点之间的跳段距离通常不是二者之间的直线距离。在各向同性的密集网络中,校正值才能合理地估算平均每跳距离,这是基于多跳的定位算法普遍存在的问题,采用DV-Hop算法过大估计了跳段的距离;未知节点计算与信标节点之间的跳数,结果都是整数,这大约增加了0.5个平均跳数的误差。通过DV-Hop算法中节点间距离度量的分析,可以发现利用这些距离没有反映出信标节点对节点位置的影响力的大小,影响了定位精度。