堆排序、堆排序优化、索引堆排序
堆排序、堆排序优化、索引堆排序
注: 堆排序、索引堆排序 都是不稳定的排序。
注:索引最大堆排序有误!!!有没有大神可以指点一二???
1、堆:
所有元素 都从索引0开始
父亲结点索引:i;
左孩子结点索引: 2i+1;
右孩子结点索引: 2i+2;
左后一个非叶子结点索引:(n-1)/2; 用于构建堆,从最后一个非叶子结点索引开始调整堆,直至到达索引为0的首个父亲结点
2、堆排序(升序为例):
共两步:
step1、构建堆
step2、原地堆排序
step1、构建堆
从最后一个非叶子结点索引开始调整堆,直至到达索引为0的首个父亲结点。
step2、原地堆排序:
每次循环,使用O(1)的时间索引到当前循环的最大值a[0],
将该最大值交换到数组末尾,
数组元素减1,
对新的堆进行调整,为下一轮循环做准备。
3、调整堆函数shiftDown()思路:
从当前父亲结点k开始,
每次比较 当前父亲结点值与该父亲结点对应的左右孩子节点中的最大值,
如果 “父亲结点值”>“最大孩子节点值”,就代表堆调整好了,提前结束循环。
如果 “父亲结点值”<“最大孩子节点值”,那么,当前"父亲结点值"更换为“最大孩子节点值"。更新父亲结点值,继续向下调整。
4、区别
4.1、普通堆排序的 shiftDown中使用“移动赋值”操作 与 “交换数据元素” 操作 区别:
使用“移动赋值”操作 比 使用"交换数据元素" 操作,的时间损耗少了2/3.
eg:shiftDown中总共进行m次循环,
—使用“移动赋值”操作:所有操作数为:m次移动+1次赋值+1个额外空间的申请,共计 m+1次 赋值操作 + 1个额外空间的申请
—使用“交换数据”操作:所有操作数为:3m次赋值+1个额外空间的申请, 共计 3m 次赋值操作 + 1个额外空间的申请
4.2、索引堆排序 与 普通堆排序 区别:
(1)定义
索引堆:数据域 与 索引域 是分开存储的。
排序过程中:数据元素的相对位置保持不变,这样可以使得 堆排序 优化为稳定的排序;改变的是索引数组的相对位置。
最后形成的索引数组,就是所谓的索引堆。
索引堆排序:
不改变原来数据域元素的位置,只是新开辟了一个索引域来代表原来数据域的相应数据进行排序,其本质还是一个堆排序。重点内容
(2)排序
比较值大小时,用的是 数据域 data数组中的元素
移动、赋值、交换时,用的是 索引域 index数组中的元素
(3)排序输出
索引堆排序:输出时,只需依次取出索引数组中对应索引的对应数据域元素,即可。
普通堆排序:依次输出,改变后的数组元素。
(4)消耗
索引堆排序 比 普通堆排序 多占用一个O(n)的int型空间,用于存放代替数据元素进行堆排序的索引数据。
(5)优点
索引堆排序与普通堆排序,优点为:
如果原来数据域中,每一个元素的数据结构很复杂,或者数据的size都很大,那么,使用普通堆排序,在移动、赋值、交换数据域的元素过程花费会非常的巨大。
而使用索引堆排序,则只是花费了一个O(n)的int类型空间,在在移动、赋值、交换操作中,都是一个int型的索引元素在参与运算,花费非常小。
5、核心代码:
/////////////////////////////////////////////////////////
//三个版本的原地堆排序
//version1 最大堆排序 shiftDown()中"交换数据元素"操作
void shiftDown(int a[], int n, int k){//以k为开始调整的父节点,自上而下调整
while (2 * k + 1 < n){//存在孩子节点时,最少存在一个“左孩子结点”
int j = 2 * k + 1;//j:左右孩子结点最大值的索引 初始化为 左孩子结点索引
if (j + 1 < n&&a[j + 1] > a[j])j += 1;//如果存在右孩子结点,且右孩子结点值大于左孩子结点值,更新孩子节点最大值索引为右孩子结点索引。
if (a[k] > a[j])break;//循环提前结束标志,当当前父节点值大于该父节点对应的最大孩子节点值时,堆调整好啦,退出循环
swap(a[k], a[j]);//交换 否则的话,交换父节点与最大值孩子节点
k = j;//更新父亲结点为当前最大值孩子节点,继续向下调整堆
}
}
void maxHeapSort(int a[], int n){
//建堆
for (int i = (n - 1) / 2; i >= 0; --i)
shiftDown(a, n, i);
//显示堆
cout << "建堆" << endl;
printArr(a, n);
//原地堆排序
for (int i = n - 1; i > 0; --i){//i:每轮循环要处理的堆元素个数
swap(a[0], a[i]);//交换最大值到数组末尾
shiftDown(a, i, 0);//调整去掉最大值后的剩余堆元素 为最大堆
}
}
//version2 最大堆排序优化 shiftDown()中使用“移动赋值”操作取代"交换数据元素" 操作
//思路源于 插入排序
void shiftDown2(int a[], int n, int k){
int tmp = a[k];
while (2 * k + 1 < n){
int j = 2 * k + 1;
if (j + 1 < n && a[j + 1] > a[j])j += 1;
if (tmp > a[j])break;
a[k] = a[j];//移动
k = j;//更新 父亲结点的索引,切记!!
}
a[k] = tmp;//赋值
}
//有问题 !!!version3 最大索引堆排序 shiftDown()中使用“移动赋值”操作
void shiftDown3(int a[], int index[], int n, int k){
int tmp_index = index[k];//开始的临时变量是 索引为k的data域中的元素,即 第索引号为k的索引域中的元素 index[k]
while (2 * k + 1 < n){
int j = 2 * k + 1;
if (j + 1 < n && a[index[j + 1]] > a[index[j]])j += 1;//a[index[j + 1]] > a[index[j]]:比较的是数据域中的元素值
if (a[tmp_index] > a[j])break;//a[tmp_index] > a[j]:比较的是数据域中的元素值
index[k] = index[j];//移动的是 索引域中元素
k = j;
}
index[k] = tmp_index;//赋值的是 索引域中元素
}
void IndexMaxHeapSort(int a[], int index[], int n){
for (int i = (n - 1) / 2; i >= 0; --i)//建堆
shiftDown3(a, index, n, i);
cout << "建堆" << endl;
printIndexMaxHeap(a, index, n);
for (int i = n - 1; i > 0; --i){//原地堆排序
swap(index[0], index[i]);
shiftDown3(a, index, i, 0);
}
}
void printIndexMaxHeap(int a[], int index[], int n){
for (int i = 0; i < n; ++i)
cout << a[index[i]] << "\t";
cout << endl;
}
//version3 end
6、完整代码,请移步我的GitHub
https://github.com/MissStrickland/maxHeapSort_indexMaxHeapSort/blob/master/main_heapSort.cpp
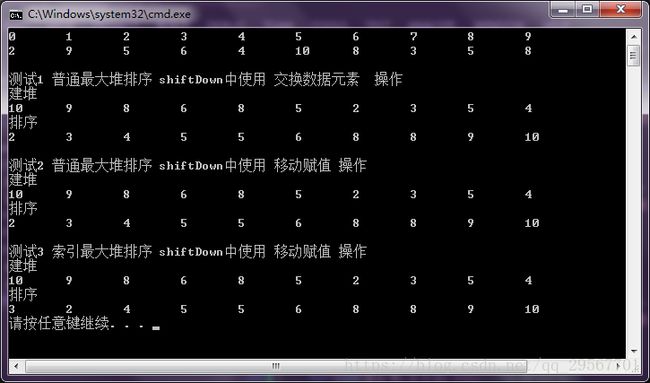
7、测试:
起始数据: 2 9 5 6 4 10 8 3 5 8
//建成堆如下:
10
/ \
9 8
/ \ / \
6 8 5 2
/ \ /
3 5 4
从测试结果看,
前俩个版本是好的,
但是,索引最大堆排序有问题!!目前找不到问题所在,还望路过的大神指点一二!!