直线检测-Radon变换、Hough变换

radon函数对应格式包括：[R,xp] = radon(I,theta);

其中，R为线积分值，xp为径向坐标，theta为投影角度；

     图像投影，就是说将图像在某一方向上做线性积分（累加求和）。如果将图像看成二维函数f(x, y)，则其投影就是在特定方向上的线性积分，比如f(x, y)在垂直方向上的线性积分就是其在x轴上的投影；f(x, y)在水平方向上的线积分就是其在y轴上的投影。通过这些投影，可以获取图像在指定方向上的突出特性，这在图像模式识别等处理中可能会用到。

Radon（拉东）算法通过定方向投影叠加，可以找到最大投影值时角度，从而确定图像倾斜角度：

                  

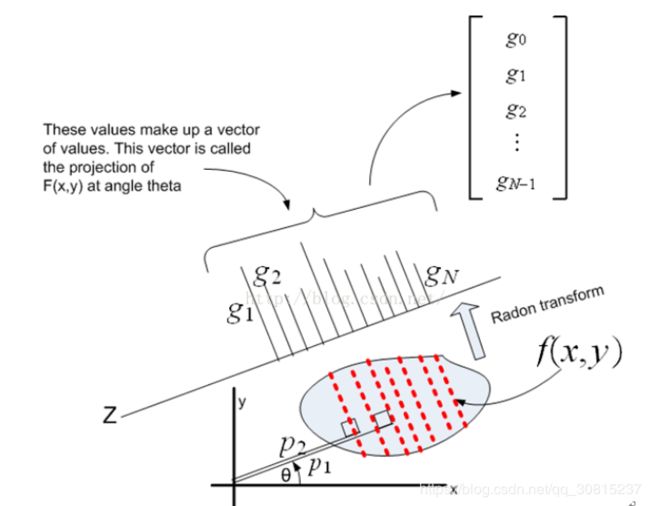
      Radon变换（拉东变换），就是将数字图像矩阵在某一指定角度射线方向上做投影变换。这就是说可以沿着任意角度theta来做Radon变换。  radon变换就是图像在不同方向上的投影。下图f(x,y)可以代表图像，R(x')就是图像向右下方的投影。数学上是按投影方向进行线积分，在图像领域就是按照投影方向累加像素就行了。

                                                              

       Radon变换的本质是将原来的XY平面内的点映射到AB平面上，那么原来在XY平面上的一条直线的所有的点在AB平面上都位于同一点。记录AB平面上的点的积累厚度，便可知XY平面上的线的存在性。这便是大家所公认的Radon变换的实质所在。 

      

数学理论

        如果我们将图像中心设为原点，用P（直线到原点的距离）和（某一特定方向）代替a、b，即，理解为图像在空间的投影，用参数表示上述直线，则有：

                                                     

假定有一个函数f(x,y)代表图像的像素，如上图所示，那么该函数过直线L区域的积分即为：

其中ds是该直线的微分。上述积分可以写为：

        因而，给定一组P和，就可以得出一个沿L(P,)的积分值，即在指定角度上的像素累加和。因此，Radon变换就是函数f (x,y)的线积分，如图所示。假如有很多平行于L的线，他们有相同的\theta，径向坐标P却不同，这就很好的印证了matlab自带的radon变换命令中每个\theta角度的Radon变换结果是有两个输出项R（一个\theta角度下的Radon变换值，即线积分值）与xp（径向坐标），两者一一对应。我们对每一条这样的平行线都做f(x,y)的线积分，会产生很多投影线，也就是说对一幅图像在某一特定角度下的Radon变换会产生N个线积分值，而每一个线积分值会对应一个径向坐标xp，各个角度的Radon变换值汇总在一起就构成一幅Radon变化图。

 

使用Radon变换检测直线，检测步骤如下：
（1）使用边缘检测函数edge函数计算二值图像；
（2）计算二值图像的Radon变换；
（3）寻找Radon变换的局部极大值，这些极大值的位置即为原始图像中直线的位置。

BW = edge(I1);
imshow(BW)
theta = 0:179;
[R,xp] = radon(BW,theta);
figure,imagesc(theta,xp,R)

      Radon变换用于直线检测，比Hough变换优越的地方在于：Radon变换可以针对非二值图像，Radon变换检测直线：灰度值高的线段会在P 空间中形成亮点，而低灰度值的直线会在P 空间中形成暗点，而Hough变换需要针对二值图像进行，仅仅积攒非0点在某一个上的个数。

from：https://blog.csdn.net/yu132563/article/details/99228303

         https://blog.csdn.net/kongxp_1/article/details/81448210

---

Hough变换

直线的表示方式

    对于平面中的一条直线，在笛卡尔坐标系中，常见的有点斜式，两点式两种表示方法。然而在hough变换中，考虑的是另外一种表示方式：使用（r,theta）来表示一条直线。其中r为该直线到原点的距离，theta为该直线的垂线与x轴的夹角。如下图所示。

也就是霍夫变换中表示一条直线的参数变成了（r,theta）。如果对位于同一直线上的n个点进行变换，原图像空间的n个点在参数空间对应得到有n条正弦曲线，并且这些曲线相交于一点。

                           

2.如何判断多个点是否在同一直线上

      当我们的对象变成点时，我们知道一个点可以发射出无数条直线，根据霍夫变换的直线表达形式，假设这个点为 i, 则通过这个点的直线我们用（ri,thetai）表示。再假设一个点为 j，则通过点 j 的一系列直线我们用（rj,thetaj）表示。我们知道两点决定一条直线，所以这两个点的直线必定有r_i=r_j,theta_i= theta_j的时候。那如果是三个点呢，假设第三个点是k，则通过k点的一系列直线为（r_k,\theta_k）,如果三点在一条直线上，那必定有某个r_i=r_j=r_k = r,theta_i = theta_j= theta_k = theta。
在霍夫变换检测直线时我们需要找到这样一样直线.

3.如何检测出直线

     假设有N个点，我们要检测其中的直线，也就是我们要找到具体的r和theata。对于上面所说的每个点可以通过无数条直线，这里我们设为n条（通常 n = 180），则我们一起可以找到N*N个（r, theata），对这N*N个（r,theata）,我们可以利用统计学，统计到在theta=某个值theta_i时，多个点的r近似相等于r_i。也就是说这多个点都在直线（r_i,theta_i）上。

4.举例说明

     如果空间中有3个点，如何判断这三个点在不在一个直线上，如果在，这条直线的位置为？这个例子中，对于每个点均求过该点的6条直线的（r,theta）坐标，共求了3*6个（r,theta）坐标。可以发现在theta=60时，三个点的r都近似为80.7，由此可判定这三个点都在直线（80.7，60）上。通过 r-o-theta 坐标系可更直观表示这种关系，如下图：图中三个点的（r,theta）曲线汇集在一起，该交点就是同时经过这三个点的直线。

      在实际的直线检测情况中，如果超过一定数目的点拥有相同的（r,theta）坐标，那么就可以判定此处有一条直线。在r-O-theta 坐标系图中，明显的交汇点就标示一条检测出的直线。如下图，可以判定出平面上的点共构成了两条直线，即检测出两条直线。

亮点对应笛卡尔坐标系下（图像）的一条直线，越亮，代表在这条直线上的非零像素数越多。（原图像是二值图像，亮度代表像素个数）

霍夫变换直线检测的步骤：

     如果一幅图像中的像素构成一条直线，那么这些像素坐标值（x, y）在霍夫空间对应的曲线一定相交于一个点，所以我们只需要将图像中的所有像素点（坐标值）变换成霍夫空间的曲线，并在霍夫空间检测曲线交点就可以确定直线了。

1、对边缘二值化图像进行霍夫空间变换；

2、在4邻域内找到霍夫空间变换的极大值；

3、对这些极大值安装由大到小顺序进行排序，极大值越大，越有可能是直线；

4、输出直线。