贪心法习题整理

贪心法

1.POJ 2393

题目 ：

The cows have purchased a yogurt factory that makes world-famous Yucky Yogurt. Over the next N (1 <= N <= 10,000) weeks, the price of milk and labor will fluctuate weekly such that it will cost the company C_i (1 <= C_i <= 5,000) cents to produce one unit of yogurt in week i. Yucky’s factory, being well-designed, can produce arbitrarily many units of yogurt each week.

Yucky Yogurt owns a warehouse that can store unused yogurt at a constant fee of S (1 <= S <= 100) cents per unit of yogurt per week. Fortuitously, yogurt does not spoil. Yucky Yogurt’s warehouse is enormous, so it can hold arbitrarily many units of yogurt.

Yucky wants to find a way to make weekly deliveries of Y_i (0 <= Y_i <= 10,000) units of yogurt to its clientele (Y_i is the delivery quantity in week i). Help Yucky minimize its costs over the entire N-week period. Yogurt produced in week i, as well as any yogurt already in storage, can be used to meet Yucky’s demand for that week.

算法思路:

本周最低成本 = min{之前生产的成本 + 存储成本，本周自产自销}

代码:

//简单的贪心法求解
#include 
using namespace std;

int main(){

    int N,S;
    int last = 10000;
    long long costs = 0;
    cin >> N >> S;

    while (N--) {
        int C,Y;
        cin >> C >> Y;
        last = min(last + S,C);
        costs += last * Y;
    }

    cout << costs << endl;

    return 0;
}

2.POJ 1328

题目:

Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.

We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.

算法思路:

1. 将每个岛能被一个雷达探测到的位置投影到x轴上，成为一个个线段。
2. 将线段按右端点坐标从小到大排序。
3. 遍历排序好的线段，只有当新线段的开始坐标 > 上一线段的结束坐标时，才增加一个雷达。同时将这个新线段的结束坐标作为“上一线段”的结束坐标。

代码:

#include 
#include 
#include 
#include 
using namespace std;

class Segment{
public:
    double start;
    double end;
    
    bool operator < (const Segment& b) const{
        return this->end < b.end;
    }
};

int main(){
    
    int n,d;
    int ID = 1;
    
    while (cin >> n >> d && n && d) {
        double x,y;
        int result = 1;
        vector seg(n);
        int i = 0;
        
        while (n--) {
            cin >> x >> y;
            if (d < y) {
                result = -1;
                continue;
            }
            double r = sqrt(d * d - y * y);
            seg[i].start = x - r;
            seg[i].end = x + r;
            i++;
        }
        
        if (result == -1){
            cout << "Case " << ID << ": " << result << endl;
            ID++;
            continue;
        }
        
        sort(seg.begin(), seg.end());
        double end = seg[0].end;
        for (vector::iterator it = seg.begin(); it != seg.end(); ++it) {
            if (it->start > end) {
                result++;
                end = it->end;
            }
        }
        cout << "Case " << ID << ": " << result << endl;
        ID++;
    }
    
    return 0;
}

3.背包问题

题目:

算法思路:

本题是物品可部分装入的背包问题，只要每次都选择单位价值最大的物体尽可能的多装即可。

python代码：

#贪心法求解背包问题，物品可部分装入
P = [12,8,1,6,5]
W = [4,6,2,3,5]
M = 4
P_perWeight = []

#因为是可部分装入，所以求出每个物体的单位价值
for i in range(len(P)):
    P_perWeight.append(P[i] / W[i])

print(P_perWeight)
result = 0
while M > 0:
    #每次都选择单位价值最大的物体尽可能的多装
    maxPos = P_perWeight.index(max(P_perWeight))
    if M - W[maxPos] >= 0:
        M -= W[maxPos]
        result += W[maxPos] * P_perWeight[maxPos]
        W[maxPos] = 0
        P_perWeight[maxPos] = -1
    else:
        result += M * P_perWeight[maxPos]
        M = 0

print(result)

4.海面船与陆地通信问题

与POJ1328一样

1. 将每个船能被一个基站通信到的位置投影到x轴上，成为一个个线段。
2. 将线段按右端点坐标从小到大排序。
3. 遍历排序好的线段，只有当新线段的开始坐标 > 上一线段的结束坐标时，才增加一个基站。同时将这个新线段的结束坐标作为“上一线段”的结束坐标。

5.工厂生产问题

题目:

算法思路:

与POJ2393 非常相似，只不过这里额外需要给出一个X数组，以记录每个月产品的生产数量。

对代码加以改动，引入一个myPos变量用来记录需要超额生产的月份即可

代码:

#工厂生产问题，贪心算法实现
C = [2,3,5,9,4]
Y = [2,2,1,3,5]
store = 1
n = len(C)
X = [0] * n
cost = 0
last = 100000
myPos = 0

for i in range(n):
    #如果超额生产的产品即使算上存储成本也比之后的某个月生产成本要低
    if last + store < C[i]:
        #引入一个myPos变量，用来记录那些需要超额生产的月份，当前月份则是i
        X[myPos] += Y[i]
    else:
        myPos = i
        #自产自销的月份
        X[i] += Y[i]
    last = min(last + store,C[i])
    cost += last * Y[i]

print(X)
print(cost)

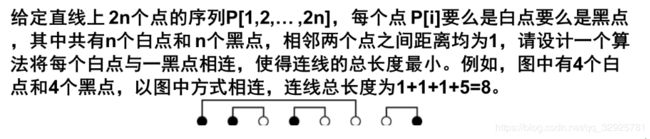
6.白点黑点连线问题

题目:

###算法思路:
对于每个白点，总是找离它最近的黑点(先向左找，再向右找)。

Python代码：

#直线上黑点与白点连线问题，贪心法解决
P = [1,1,0,1,0,0,0,1]
#P = [0,1,1,0,0,1]
N = len(P)
totalLength = 0

for i in range(N):
    if P[i] != 0:
        continue

    flag = False
    j = i - 1
    #先向左找最近的黑点
    while j >= 0:
        if P[j] == 1:
            totalLength += i - j
            #用过的黑点就将P[j]置为-1
            P[j] = -1
            flag = True
            break
        j = j - 1
    
    if flag == True:
        continue
    
    j = i + 1
    #再向右找
    while j < N:
        if P[j] == 1:
            totalLength += j - i
            #用过的黑点就将P[j]置为-1
            P[j] = -1
            break
        j = j + 1


print(totalLength)