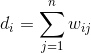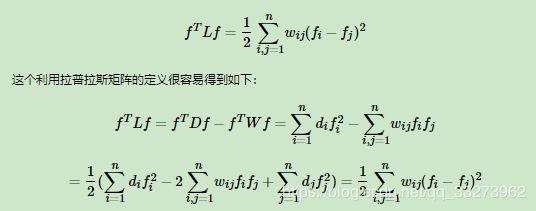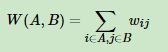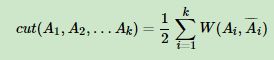谱聚类算法简单理解
一、算法思想
谱聚类是基于图论的知识所演化出的算法,在聚类中广泛使用。主要思想是将所有的数据看成空间中的点,这些点之间可以用边连接起来,距离较远的两点之间边的权重值较低,距离较近的两点间边的权重值较高,然后通过对所有数据点组成的图进行切图,让切图后不同子图间边的权重之和尽可能低,子图内边的权重之和尽可能高,从而达到聚类的目的。
图一
二、基础知识
1、无向权重图
对于一个图G,我们定义点的集合V和边的集合E来描述,记为G(V,E),其中V=(v1, v2,...,vn)。定义wij是点vi和vj之间的权重,对于无向图,则有wij=wji。若两点vi和vj之间有边连接,则wij>0,若没有则wij=0。图中任意一点vi的度di就是与之相连的所有边的权重之和,即
接着,我们利用所有点的度构建一个NxN的度矩阵D,它是一个对角矩阵,定义如下
利用所有点之间的权重值,我们可以得到一个NxN的邻接矩阵,wij就是我们邻接矩阵第i行和第j列的权重wij。
2、相似度矩阵
事实上,在谱聚类中我们并没有直接给出权重,因此无法直接构建邻接矩阵。因此,在谱聚类中的基本思想是,距离较远的两点之间权重值较低,距离近的权重值较高,在定量的给定权重值时,我们是通过样本点距离度量的相似度矩阵S来得到邻接矩阵W的。为了得到相似度矩阵,从而求出W,我们一般有三类方法:![]() -近邻法,k-近邻法和全连接法。
-近邻法,k-近邻法和全连接法。
(1)对于![]() -近邻法,设置一个距离阈值
-近邻法,设置一个距离阈值![]() ,然后用欧氏距离Sij度量任意两点间的距离,即相似度矩阵
,然后用欧氏距离Sij度量任意两点间的距离,即相似度矩阵![]() ,然后根据sij和
,然后根据sij和![]() 的大小关系,来定义邻接矩阵W如下:
的大小关系,来定义邻接矩阵W如下:
(2)对于k近邻法,我们利用KNN算法遍历所有样本点,取每个样本最近的k个点作为近邻,只有和样本距离最近的k个点之间的wij>0,但这种方法造成重构后的邻接矩阵W不是堆成的,,为解决这一问题,可以使用如下两种方法来解决:
(3)对于全连接法 (使用最普遍),由于所有点之间的权重都大于0,所以叫全连接法。我们使用不同的核函数来定义边权重,常用的有多项式核函数,高斯核函数和Sigmoid核函数,最常用的是高斯核函数RBF,此时相似度矩阵和邻接矩阵相同:
3、拉普拉斯矩阵
拉普拉斯矩阵的定义是L=D-W。D为度矩阵,W为邻接矩阵。拉普拉斯具有一些较好的性质,如下:
(1)是对称矩阵
(2)所有的特征值都是实数
(3)对于任意向量Z,有:
(4)是半正定的,且对应的n个实数特征值都大于等于0,且最小的特征值为0,。
4、无向图切图
对于无向图G进行切图,将图切成k个子图,每个子图点的集合为A1,A2,...,Ak,满足![]()
对任意两个字图A和B,我们定义 它们之间的切图权重为:
对于k个子图点的集合:A1,A2,...Ak,我们定义切图为:
但是如何使得子图内权重高,子图间权重低,我们需要运用谱聚类的方法进行切图,找到最优化方法。
三、谱聚类操作
1、Normarized cut方法
该方法同时考虑最小化cut边和划分平衡,以免出现图一种的单独H的情况,划分标准是:子图各个端点的度之和。
2、Min cut方法
如上述方法中的计算方法,优化目标函数如下:
3、Ratio Cut方法
该方法同时考虑最小化cut边和划分平衡,最优化目标函数为:
四、算法流程
1、构建相似度矩阵S
2、根据相似度矩阵构建邻接矩阵W和度矩阵D
3、计算拉普拉斯矩阵L,并求出标准化后的拉普拉斯矩阵D-1/2LD-1/2
4、计算D-1/2LD-1/2最小的k1个特征值所对应的特征向量f,并对f组成的矩阵按行标准化,最终组成nxk1维的特征矩阵F
5、将F中的每一行作为一个样本,共n个样本,使用聚类方法进行聚类,聚类维数为k2
6、得到簇划分C(c1,c2,...,ck2)
五、补充
上面,我们讲了拉普拉斯矩阵是通过L=D-W来构造,拉普拉斯矩阵还可以通过相似度矩阵来构造,方法如下:
相似度矩阵是由权值矩阵得到的:
注:在第一种方法中,求解的是Laplacian矩阵的前![]() 个最小特征值对应的特征向量,在第二种方法中,求解的是Laplacian矩阵的前
个最小特征值对应的特征向量,在第二种方法中,求解的是Laplacian矩阵的前![]() 个最大特征值对应的特征向量
个最大特征值对应的特征向量
谱聚类算法的主要优点有:
1)谱聚类只需要数据之间的相似度矩阵,因此对于处理稀疏数据的聚类很有效。这点传统聚类算法比如K-Means很难做到
2)由于使用了降维,因此在处理高维数据聚类时的复杂度比传统聚类算法好。
谱聚类算法的主要缺点有:
1)如果最终聚类的维度非常高,则由于降维的幅度不够,谱聚类的运行速度和最后的聚类效果均不好。
2)聚类效果依赖于相似矩阵,不同的相似矩阵得到的最终聚类效果可能很不同。
参考:
https://www.cnblogs.com/pinard/p/6221564.html
https://www.cnblogs.com/sparkwen/p/3155850.html