深度优先(DFS)、广度优先(BFS)、一致代价(UCS)搜索算法的实现(附代码)
Introduction
一、 深度优先搜索算法
从一个顶点v出发,首先将v标记为已遍历的顶点,然后选择一个邻接于v的尚未遍历的顶点u,如果u不存在,本次搜素终止。如果u存在,那么从u又开始一次DFS。如此循环直到不存在这样的顶点。
假设我们建立如下树

搜索过程如下:

首先编码,令S=1、a=2、b=3、c=4、d=5、e=6、f=7、g=8、h=9、r=10、p=11、q=12
重复点不再搜索,所以12个点最多24步搜索完毕
代码主要部分为
- 建立结构体,包含序号、状态、发现时刻、完成时刻、上下节点
- 字符与数字的互相转换函数
- DFS函数:根据判断下一个节点是否被发现过来搜索,若搜索过将会被标记,若没有节点将返回上一节点,并寻找新的节点

- 并对节点路径显示
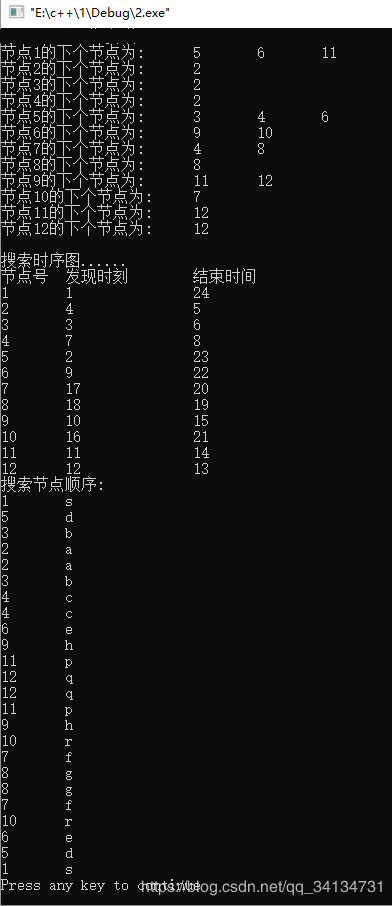
DFS实现代码
#include
#include
#include
#include
#include
using namespace std;
struct Node{//节点结构体
int Num;//节点序号,与节点一一对应
int State;//三种状态,0表示未被发现,1表示正在处理,2表示处理完成
int Find;//发现节点的时刻
int Solve;//完成对节点处理的时刻
vector next;//存储所有的邻接节点
Node* pre;
Node(int x):State(0),Num(x),Find(0),Solve(0),pre(NULL){
}
};
void insert(Node* L,Node* n)
{
L->next.push_back(n);
}
void display(Node* L)//显示该节点的所有邻接节点
{
int n=L->next.size();
for(int i=0;inext)[i]->Num<<" ";
}
void display2(int num)
{switch(num){
case 1:
cout<<"s"<Find=time;
u->State=1;
int n1=u->next.size();
for(int i=0;inext)[i];//判断下一个节点是否被处理过,若未被处理则继续
if(v->State==0)
{
v->pre=u;//并存储上一节点
dfs_v(a,n,v);//继续往下搜索
}
}
u->State=2;
time++;
u->Solve=time;
}
void dfs(Node* a[],int n) //dfs搜索函数
{
for(int i=0;iState==0)
dfs_v(a,n,u);
}
}
int main()
{
Node* a[12];
int b[12][12]={{5,6,11},{2},{2},{2},{3,4,6},{9,10},{4,8},{8},{11,12},{7},{12},{12}};
cout<<"By drs"<next.push_back(a[b[j][i]-1]);
cout<<"节点"<Num<<" "<Find<<" "<Solve<Find))||(n==(a[m]->Solve))){
cout<Num<<" ";
display2(a[m]->Num);
break;
}
}
n++;
}
}
二、 广度优先搜索算法
按层次来遍历的,先是根节点,然后是第二层子节点,依次是第三层子节点,将节点分别放入队列中,每次从队列中探出首元素,遍历后的点放入closed表中,还未遍历的店放入open表中,当open表为空时,则整个数遍历完全。
假设我们建立如下树

搜索过程如下:
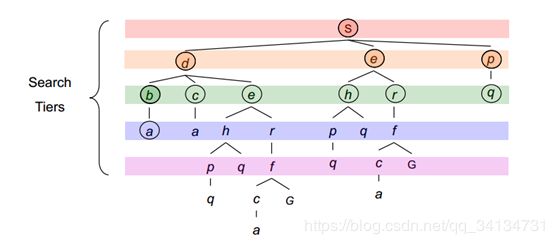
代码主要部分为
- 建立结构体,包含序号、状态、发现时刻、上下节点
- 字符与数字的互相转换函数
- BFS函数:首先按照层等级排列,一个层的顺序依次开始,然后根据本层节点搜索下一层节点,并判断下一层节点是否被搜索,若搜索过将跳过,并不能搜索。

- 并对节点路径显示、
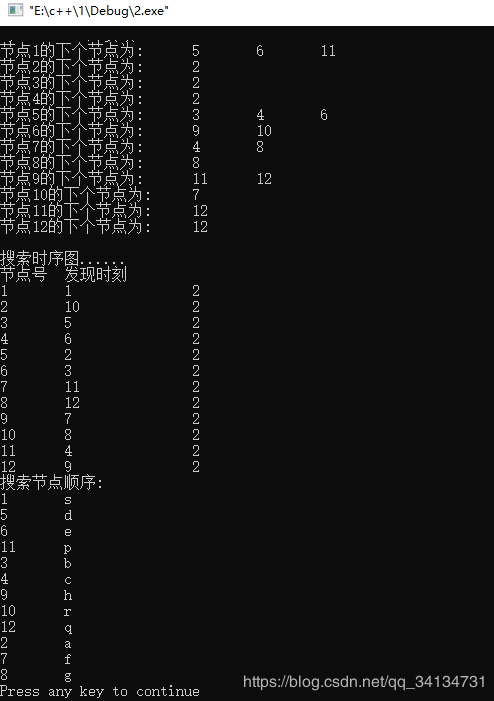
BFS实现代码
#include
#include
#include
#include
#include
using namespace std;
struct Node{//节点结构体
int Num;//节点序号,与节点一一对应
int State;//三种状态,0表示未被发现,1表示正在处理,2表示处理完成
int Find;//发现节点的时刻
vector next;//存储所有的邻接节点
Node* pre;
Node(int x):State(0),Num(x),Find(0),pre(NULL){
}
};
void insert(Node* L,Node* n)
{
L->next.push_back(n);
}
void display(Node* L)//显示该节点的所有邻接节点
{
int n=L->next.size();
for(int i=0;inext)[i]->Num<<" ";
}
void display2(int num)
{switch(num){
case 1:
cout<<"s"<State=2;
time++;
u[p]->Find=time;
for(int q=0;q<(u[p]->next.size());q++){//对当前层的某一个节点的下一层节点处理
if((u[p]->next)[q]->State==0) {//判断是否搜索过
c[ww]=(u[p]->next)[q];//添加到下一层
ww++;//下一层数量加
(u[p]->next)[q]->State=1;//状态为正在处理
}
}
}
if(ww==0) return 0;
bfs_v(c,ww);
}
void main()
{
Node* a[12];
Node* DD[12];
int b[12][12]={{5,6,11},{2},{2},{2},{3,4,6},{9,10},{4,8},{8},{11,12},{7},{12},{12}};
cout<<"By drs"<next.push_back(a[b[j][i]-1]);
cout<<"节点"<State=2;
DD[0]=a[0];
bfs_v(DD,1);
cout<Num<<" "<Find<<" "<State<Find))){
cout<Num<<" ";
display2(a[m]->Num);
break;
}
}
n++;
}
}
三、 一致代价搜索算法
在BFS的基础上,一致代价搜索不在扩展深度最浅的节点,而是通过比较路径消耗,并选择当前代价最小的节点进行扩展,因此可以保证无论每一步代价是否一致,都能够找到最优解。
假设我们建立如下树
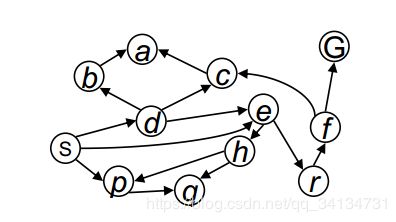
搜索过程如下:
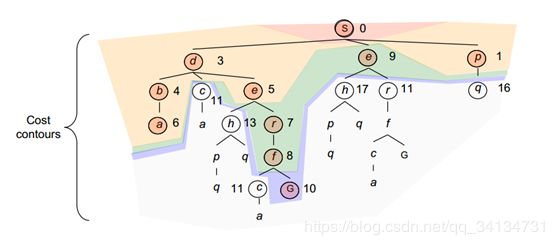
代码(基于BFS完成)主要部分为
- 建立结构体,包含序号、状态、发现时刻、上下节点
- 字符与数字的互相转换函数
- UCS函数:首先按照层等级排列,一个层的顺序依次开始,然后根据本层节点搜索下一层节点,若在当前层的某一个节点的下一层发现目标节点,则开始寻求路径,根据前面保存的上下层关系返回到s层(出发点),关键部分代码如下。

- 并对节点路径显示、
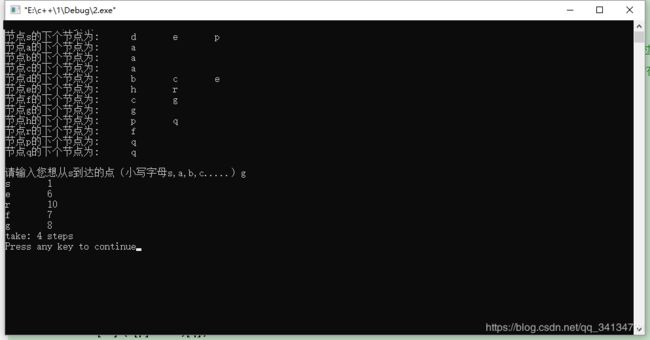
UCS实现代码
#include
#include
#include
#include
#include
using namespace std;
struct Node{//节点结构体
int Num;//节点结构体,与节点一一对应
int State;//三种状态,0表示未被发现,1表示正在处理,2表示处理完成
int Find;//发现节点的时刻
vector next;//存储其对应的下一个节点
Node* pre;//储存前一个节点,需要赋值完成
Node(int x):State(0),Num(x),Find(0),pre(NULL){//初始化
}
};
void display2(int num)//序号与字母转换显示
{switch(num){
case 1:
cout<<"s";break;
case 2:
cout<<"a";break;
case 3:
cout<<"b";break;
case 4:
cout<<"c";break;
case 5:
cout<<"d";break;
case 6:
cout<<"e";break;
case 7:
cout<<"f";break;
case 8:
cout<<"g";break;
case 9:
cout<<"h";break;
case 10:
cout<<"r";break;
case 11:
cout<<"p";break;
case 12:
cout<<"q";break;
default:cout<next.push_back(n);
}
void display(Node* L)//显示该节点的所有邻接节点
{
int n=L->next.size();
for(int i=0;inext)[i]->Num);
cout<<" ";
}
}
int Judge(char a){
switch(a){
case 's': return 1;
case 'a': return 2;
case 'b': return 3;
case 'c': return 4;
case 'd': return 5;
case 'e': return 6;
case 'f': return 7;
case 'g': return 8;
case 'h': return 9;
case 'r': return 10;
case 'p': return 11;
case 'q': return 12;
default:cout<State=2;
u[p]->Find=time;
for(int q=0;q<(u[p]->next.size());q++){//当前节点级的每一个节点的下一个节点,并排除已经被上一级和同级的下一级发现过得节点
if((u[p]->next)[q]->State==0) (u[p]->next)[q]->pre=u[p];//若是未被搜索过得节点,才可以用来确定上一级节点,并储存上一级节点数据
if((u[p]->next)[q]->Num==aim) {//序号为8即s,为要寻找的点
mm=(u[p]->next)[q];//如果是则开始找寻前级节点
follow[time]=mm->Num;
for(int qq=0;qqpre;
follow[time-qq-1]=mm->Num;//存储在数组中
// cout<Num<<" ";
// display2(mm->Num);
}
for(int qc=0;qcNum<Num);
// cout<<(u[p]->pre)->Num<next)[q])->pre).Num<next)[q]->State==0) {//若是未处理点,则保存到数组c,并变为正在处理状态
c[ww]=(u[p]->next)[q];
ww++;
(u[p]->next)[q]->State=1;
}
}
}
ucs(c,ww,aim);
}
void main()
{
Node* a[12];
Node* DD[12];
char abc;
int b[12][12]={{5,6,11},{2},{2},{2},{3,4,6},{9,10},{4,8},{8},{11,12},{7},{12},{12}};
cout<<"By drs"<next.push_back(a[b[j][i]-1]);
cout<<"节点";display2(j+1);cout<<"的下个节点为: ";
display(a[j]);
cout<State=2;
DD[0]=a[0];
cout<>abc;
// cout<