四、递归、回溯、分治(小象)
目录
78.求子集
递归法
利用位运算法
90.子集II
40.组合总和II
22.括号生成
51.N皇后问题
315.计算右侧小于当前元素的个数
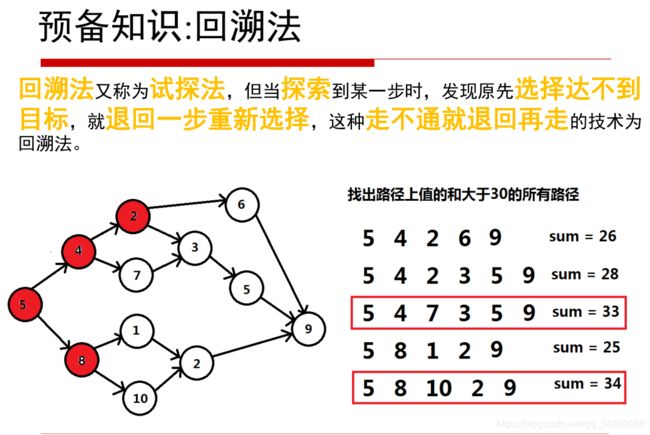
回溯法:用递归来实现回溯法。
78.求子集
递归法
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: nums = [1,2,3] 输出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]
class Solution {
public:
vector> subsets(vector& nums) {
vector> result;
vector item; //存储子集
result.push_back(item);
generate(0,item,result,nums);
return result;
}
void generate( int i,vector &item,vector> &result,vector& nums){
if(i >= nums.size()){
return ;
}
item.push_back(nums[i]);
result.push_back(item);
generate(i+1,item,result,nums);
item.pop_back();
generate(i+1,item,result,nums);
}
}; 利用位运算法
左移1位:等于乘以2
右移1位:等于除以2
要表示2^n = 1<< n (1向左移动n位)
'&' !!!位运算的时候,不需要转换成二进制!直接用十进制就可以了!
class Solution {
public:
vector> subsets(vector& nums) {
vector> reslut;
int result_num = 1< item; //这不是重定义了吗?没太懂为啥没错呢。
for(int j = 0; j < nums.size();j++){
if(i&(1< 90.子集II
给定一个可能包含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: [1,2,2] 输出: [ [2], [1], [1,2,2], [2,2], [1,2], [] ]
思考:可以添加一个set集合 ,里面存放的是vector
比如:set
原来的nums = [2,1,2,2]
可能会因为选择的位置不同 ,选出来[2,1] [1,2] 但是因为子集的无序性,其实是一个子集。所以用set来查找,但是[2,1] [1,2] 用set也查找不出来,因为他的确是两个不同的,如果我们在之前把nums排序,就不会出现[2,1] [1,2] ,而都是[1,2]了,这样就可以检测出来了。
key : 1、要把nums先进行排序,用sort();2、要设置一个set
class Solution {
public:
vector> subsetsWithDup(vector& nums) {
vector> result;
vector item;
//res_set这个set集合只是为了检测当前要传入的子集在不在以前已经出现了
set> res_set;
sort(nums.begin(),nums.end());
res_set.insert(item);
result.push_back(item);
generate(0,item,result,nums,res_set);
return result;
}
void generate(int i ,vector &item,vector> &result,
vector & nums, set>& res_set){
if(i >= nums.size()) return ;
item.push_back(nums[i]);
//查找到res_set.end()表示没有查到 这个时候才应该把这个子集添加到result之中
if(res_set.find(item) == res_set.end()){
res_set.insert(item);
result.push_back(item);
}
generate(i+1,item,result,nums,res_set);
item.pop_back();
generate(i+1,item,result,nums,res_set);
}
}; 40.组合总和II
思考:回溯过程中加入剪枝 会大幅度降低算法效率和时间复杂度
sum > target 直接 修剪掉
在深度搜索使用剪枝很常用
class Solution {
public:
vector> combinationSum2(vector& candidates, int target) {
vector> result;
set> res_set;
vector item;
sort(candidates.begin(),candidates.end());
generate(0,0,item,result,res_set,candidates,target);
return result;
}
//傻逼了。。。忘记传引用 我说为啥这个还有重复的集合呢!!! set忘记传引用
void generate(int i ,int sum ,vector &item, vector> &result,
set> &res_set,vector& candidates, int target) {
if(i >= candidates.size()||sum > target){
//跳出循环的条件 肯定是和已经大于了目标值 而不是等于
//还有 是或而不是与。。。只要有一个不满足就可以跳出来了
return ;
}
item.push_back(candidates[i]);
sum += candidates[i];
if(sum == target && res_set.find(item) == res_set.end()){
//要添加的是正好满足条件的集合,而不是在进行循环累加
//比如 [1,7] 加起来正好等于8才可以添加进去,而不是一个一个的往集合中添加
//元素在判断 22.括号生成
首先回答问题:如果有N组括号,求生成的全部集合?
若有2组括号,全部生成的可能集合总共有1<<4,一共16种。
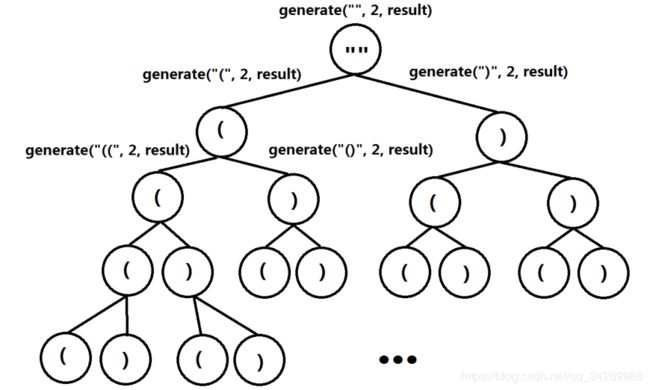
一开始传入的是" " 空字符串,每次选择"("或者是")",如下图:
#include
#include
#include
using namespace std;
void generate(string item,int n ,vector& Result){
if(item.size() == 2 * n){
Result.push_back(item);
return ;
}
generate(item+"(",n,Result);
generate(item+")",n,Result);
}
void main(){
vector result;
generate("",2,result);
for(int i = 0 ; i < (1<<4);i++){
cout< key:
1、生成合法的括号对,则"(" 和 ")"成对出现,若N =2 ,则左括号2个,右括号两个。
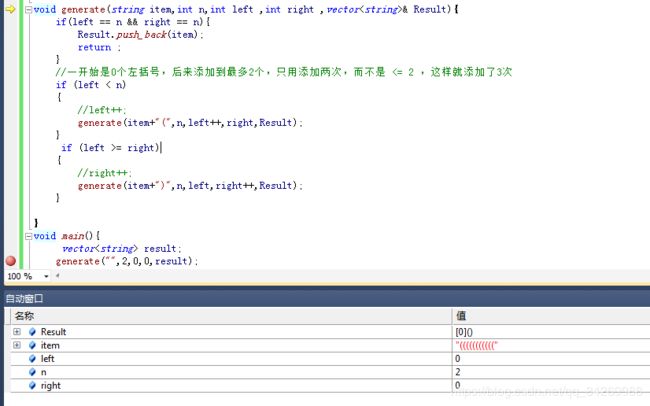
2、若是合法的括号对,则"("的数量不小于")"的时候才可能添加")". //更正!!!不是不小于啊!是严格的大于")"的时候才可以添加,举例子当都只0的时候?难道可以先添加"("吗?
3、在递归回溯的过程中不要再调用函数中使用++运算符//(否则如下图 left不变化 但是一直添加。。)
4、见2!调BUG N久。。。我说为什么一直就有问题呢!
class Solution {
public:
vector generateParenthesis(int n) {
string item;
vector result;
generate(item,n,0,0,result);
return result;
}
void generate( string item,int n ,int left/*此时的左括号数*/ ,int right,vector &result){
if(left == n&& right ==n ){
result.push_back(item);
return ;
}
if(left < n ){
generate(item+"(",n,left+1,right,result);
}
if(left > right){
generate(item+")",n,left,right+1,result);
}
}
}; 51.N皇后问题
思考: = = !早都在vs上调好了!弄了一晚上!!!因为几个小BUG自己没注意,写到LeetCode上总是出错。
1、首先要写一个函数push_on_board(int x,int y ,vector
2、输出的是字符串棋盘,所以要用一个vector
3、用递归来回溯比较简单,就按照行来放置皇后,然后按照列遍历,看看这一列能不能放啊之类的。退出的结果就是目前放置的皇后数目已经是n个了。
4、遇到的很头疼的地方!
1、LeetCode显示no function match ...我服了 我找了N久,我这从vs运行的怎么就没有函数匹配了,试了把函数放在类外面,又查了半天也没用。后来别人才给我指出来!我函数的变量类型声明错了!vector
2、总是显示“ reference binding to null pointer of type 'value_type”,简直了!我想半天这result二维数组也没法赋初值啊!查好久!后来才看到是 vector
class Solution {
public:
vector> solveNQueens(int n) {
vector> result;
vector item ;
vector> checkerBoard(n);
for(int i =0 ; i< n ;i++){
// checkerBoard.push_back(vector());
for(int j = 0 ; j< n ;j++){
checkerBoard[i].push_back(0);
}
item.push_back("");
item[i].append(n,'.');
}
//result.push_back(item);
generate(0,n,checkerBoard,item,result);
return result;
}
void push_on_checkerBoard(int x, int y ,vector>&checkerBoard ){
const int dx[] = {1,1,0,-1,-1,-1,0,1};
const int dy[] = {0,-1,-1,-1,0,1,1,1};
checkerBoard[x][y] = 1;
for(int i = 1 ; i = 0 && newY < checkerBoard.size()&&newY >= 0 ){
checkerBoard[newX][newY] = 1;
}
}
}
}
void generate(int k /*完成了几个皇后放置*/, int n , vector> &checkerBoard, vector &item, vector> &solution){
if(k==n){
solution.push_back(item);
return ;
}
for(int i = 0; i< n ;i++){
if(checkerBoard[k][i] == 0){
vector> mark = checkerBoard;
push_on_checkerBoard(k,i,checkerBoard);
item[k][i] = 'Q';
generate(k+1,n,checkerBoard,item,solution);
checkerBoard = mark;
item[k][i] = '.';
}
}
}
};
315.计算右侧小于当前元素的个数
首先是回顾了“归并排序”,一开始看书的时候觉得好难,后来自己实现了就发现还是挺简单的。
基本的操作就两个:
1、两个有序的数组进行合并成为一个有序的数组。
-->两个计数器,同时指向数组的首元素,然后比较,如果vec1[i] <= vec2[j],那么把vec[i]这个元素存储到新开辟的vec之中,同理如果大于就放入vec[j],同时应该把当前的计数器后移一位,判断终止条件就是其中某一个数据已经使用完了,那么直接把另一个数组接到新的vec尾部就可以了。
缺点:“大概就是新开辟的空间吧”~
2、如果是无序的数组,传入进来用归并排序,首先应该使用递归的思想,把传入进来的vec进行验证,如果它的元素小于2,意味着只有1个或者0个元素,就直接求解;否则的话就把vec一分为二,变成sub_vec1,sub_vec2。然后再足够小的规模的时候再使用归并排序。这里要理解递归的含义!
3、题目的难点就在于“排序了之后,原先元素的位置发生了改变,再想对应回去它本来位置的正确逆序数就很苦难。”....
所以采用元素和位置进行绑定,使用pair就可以了,把原始的nums变成vector
5、还有一点需要反思的地方,就是我在分治的时候,把原始的问题变成了两个子问题,就直接去调用递归排序想要解决问题,实际上这里反应了我对递归的不理解,应该是一直调用,等到足够小到一定规模的时候,才使用真正解决问题的手段——归并,而不是直接变成两个子问题就归并!~
vector> sub_vec1;
sub_vec1.assign(vec.begin(), vec.begin() + mid);
vector> sub_vec2;
sub_vec2.assign(vec.begin()+ mid, vec.end());
//sortTheOrder(sub_vec1, sub_vec2, vec);没有真理解递归的意义
smallerNumber(sub_vec1, count);
smallerNumber(sub_vec2, count);
vec.clear();
sortTheOrder(sub_vec1, sub_vec2, vec, count); 6.还有个问题就是我一开始用迭代器做可以通过小数据的案例,但是大数据量就没法过,测试的数据集有两个计算错了,真不懂。。我也没有对子vector进行修改啊,为什么它的迭代器来操作就有问题呢。。不太懂。。。放上这个失败的代码。。。看看以后能不能找到解决的方法。
class Solution {
public:
vector countSmaller(vector& nums) {
vector counts;
vector > vec;
for(int i = 0; i >& vec,vector&count) {
if (vec.size() < 2) {
return;
}
int mid = vec.size() / 2;
vector> sub_vec1;
sub_vec1.assign(vec.begin(), vec.begin() + mid);
vector> sub_vec2;
sub_vec2.assign(vec.begin()+ mid, vec.end());
//sortTheOrder(sub_vec1, sub_vec2, vec);没有真理解递归的意义
smallerNumber(sub_vec1, count);
smallerNumber(sub_vec2, count);
vec.clear();
sortTheOrder(sub_vec1, sub_vec2, vec, count);
}
void sortTheOrder(vector>& sub_vec1,
vector>& sub_vec2,
vector>& vec,
vector &count) {
vector>::iterator iter1 = sub_vec1.begin();
vector>::iterator iter2 = sub_vec2.begin();
while (iter1 != sub_vec1.end() && iter2 != sub_vec2.end()) {
if (*iter1 <= *iter2) {
vec.push_back(*iter1); //count[i] += j
count[iter1->second] += iter2 - sub_vec2.begin();
iter1++;
}
else {
vec.push_back(*iter2);
iter2++;
}
}
if (iter1 == sub_vec1.end()) {
vec.insert(vec.end(), iter2, sub_vec2.end());
}
if (iter2 == sub_vec2.end()) {
for (auto i = iter1; i != sub_vec1.end(); i++) {
//iter1->first = iter1->first + (int)sub_vec2.size();
count[iter1->second] += (int)sub_vec2.size();
}
vec.insert(vec.end(), iter1, sub_vec1.end());
}
}
}; 7.最后附上正确的代码:
class Solution {
public:
vector countSmaller(vector& nums) {
vector counts;
vector > vec;
for(int i = 0; i >& vec,vector&count) {
if (vec.size() < 2) {
return;
}
int mid = vec.size() / 2;
vector> sub_vec1;
sub_vec1.assign(vec.begin(), vec.begin() + mid);
vector> sub_vec2;
sub_vec2.assign(vec.begin()+ mid, vec.end());
//sortTheOrder(sub_vec1, sub_vec2, vec);没有真理解递归的意义
smallerNumber(sub_vec1, count);
smallerNumber(sub_vec2, count);
vec.clear();
sortTheOrder(sub_vec1, sub_vec2, vec, count);
}
void sortTheOrder(vector>& sub_vec1, vector>& sub_vec2,
vector>& vec, vector &count) {
int i = 0, j = 0;
while (i != sub_vec1.size()&&j != sub_vec2.size()) {
/*if (*iter1 <= *iter2)*/
if(sub_vec1[i].first <= sub_vec2[j].first)
{
vec.push_back(sub_vec1[i]); //count[i] += j
count[sub_vec1[i].second] += j;
i++;
}
else {
vec.push_back(sub_vec2[j]);
j++;
}
}
while (i != sub_vec1.size()) {
vec.push_back(sub_vec1[i]);
count[sub_vec1[i].second] += j;
i++;
}
while (j!= sub_vec2.size()) {
vec.push_back(sub_vec2[j]);
j++;
}
}
}; 总结:这几个代码难度感觉都好大。。我弄了好久才弄完 = = 感觉要是自己刷题还是先从medium挨个做吧!不过收获也很大!再接再厉咯!