剑指offer面试题38字符串全排列

 问题1：

输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。（输入一个字符串,长度不超过9(可能有字符重复),字符只包括大小写字母）

分析：这属于输入字符串中可能有重复字符，所有重复的组合只打印一次（比如“aa”，只输出"aa"）

#include 
class Solution {
public:
    vector Vec;
    void Permutation(string s,unsigned int pbegin)
    {
        if(pbegin==s.size()-1)
            Vec.push_back(s);
        else
        {
        for(unsigned int i=pbegin;i<=s.size()-1;++i)
        {
            if(i!=pbegin&&(s[i]==s[pbegin]||s[i]==s[i-1]))
                continue;
             swap(s[pbegin],s[i]);
             Permutation(s,pbegin+1);
             swap(s[pbegin],s[i]);
        }
        }
    }
    vector Permutation(string str) {
        if(str.size()<=0)
            return{};
        Permutation(str,0);
        sort(Vec.begin(),Vec.end());   //那字典序排序
        return Vec;
    }
};

 

问题2 

继续上题，输入字符串可能重复，所有组合包括重复的字符串都打印出(输入"aa"，输出"aa"，"aa")，把上面程序的for循环里的if判断语句去掉即可

问题3.

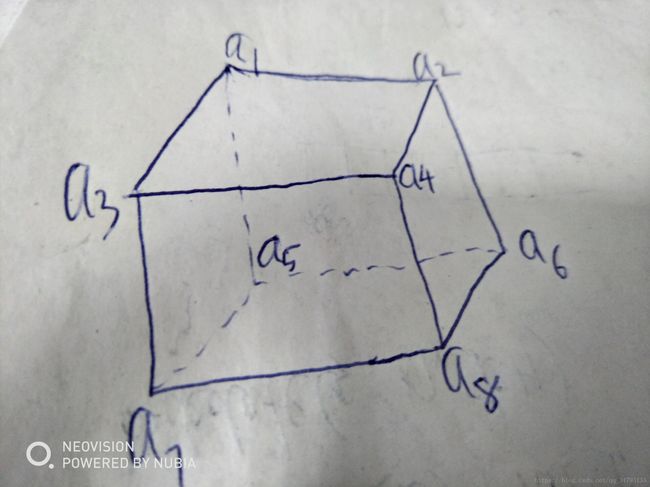
输入一个含有8个数字的数组，判断有没有可能把这8个数字分别放入正方体的8个顶点上，使得正方体的三组相对的面的4个顶点的和都相等

分析：可以往容器条件是：begin == str.size() - 1外加：(a1+a3+a5+a7=a2+a4+a6+a8)&&(a1+a2+a3+a4=a5+a6+a7+a8)&&(a1+a2+a5+a6=a3+a4+a7+a8)

在最后输出vector时候作为是否输出的判断条件

 

另一类问题，求所有组合

问题4

引申：若不是求字符的所有排列而是求字符的所有组合？

     分析：比如输入“abc”，他们的组合应该是a、b、c、ab，ac、bc、abc、当交换字符串中两个字符时候虽然得到不同的两个排列，但却是同一个组合。比如ab和ba是不同排列，但是同一组合。

如果输入n个字符，求长度为m的组合（1<=m<=n），若组合里包含第一个字符，则下步在剩余的n-1个字符里选m-1个；若组合不包括第一个字符，则从其余n-1个字符字符选m个字符。也就是，把n个字符的组成的长为m的组合问题分解成两个子问题，求n-1个字符长度是n-1的组合，求n-1个字符长度是m的组合

#include
#include
#include
using namespace std;
 
//从头扫描字符串得到第一个字符，针对第一个字符，有两种选择
//把这个字符放到组合中去，接下来我们需要在剩下的n-1个字符中选取m-1个字符；
//如果不把这个字符放到组合中去，则需要在剩下的n-1个字符中选取m个字符 
void Combination(char* string, int number, vector& result)
{
	if (number == 0)
	{
		vector::iterator iter = result.begin();
		for (; iter < result.end(); ++iter)
			cout << (*iter);
		cout << endl;
		return;
	}
	if (*string == '\0')
		return;
	result.push_back(*string);
	Combination(string + 1, number - 1, result);//把这个字符放到组合中去，接下来我们需要在剩下的n-1个字符中选取m-1个字符
	result.pop_back();
	Combination(string + 1, number, result);//不把这个字符放到组合中去，则需要在剩下的n-1个字符中选取m个字符 
}
 
void Combination(char* string)
{
	if (string == NULL)
		return;
	int length = strlen(string);
	vector result;
	for (int i = 1; i <= length; i++)
	{
		Combination(string, i, result);
	}
}
 
int main()
{
	char s[] = "abc";
	Combination(s);
	system("pause");
	return 0;
}

问题5 八皇后问题

8*8的棋盘上摆8个皇后，，任意两个不在同一行，同一列，同一条对角线，

分析：若设一个a[0]   a[1]......a[7]的数组，每个数组放0~7中的一个数，且数组中没重复的元素，就可以保证不同行，不同列。那怎样不同对角线，(i-j==array[i]-array[j])||(j-i==array[j]-array[i])则在一条对角线

八皇后问题之前用回溯法之前整理过

https://blog.csdn.net/qq_34793133/article/details/80721269

问题6  问题1是不是也可以用回溯法？

 

 

 

 

参考：https://blog.csdn.net/geekmanong/article/details/50945067