翻译:A Unified Approach to Route Planning for Shared Mobility(未完成)
文章目录
- 摘要
- 1.介绍
- 2.相关工作
- 3.问题陈述
- 3.1符号和定义
- 3.2 统一目标与URPSM问题
- 3.3 难度分析
- 4.基于DP的插入
- 4.1准备工作
- 4.2 基本插入
- 4.3 基于朴素DP的插入
- 4.3.1 在$O(1)$时间内计算$\Delta_{i,j}$
- 4.3.2 在$O(1)$时间内检查路线可行性
- 4.3.3 算法草图
- 4.4 线性基于DP的插入
- 4.4.1 列举交付地点
- 4.4.2 在$O(1)$时间找到最佳拾取位置
- 4.4.3 算法草图
- 5. 基于插入的解决方案
- 5.1 决策阶段
- 5.1.1 计算$\Delta^*$的下界
- 5.1.2 算法草图
- 5.2 设计阶段
- 5.2.1 修剪候选工人
- 5.2.2 找到最佳工人
- 5.3 算法草图
- 6. 实验性研究
- 6.1 实验设置
- 6.2 实验结论
- 7. 总结
- 8.参考资料
摘要
共享移动应用程序出现了大幅增长,例如共享汽车,食品配送和众包包裹递送。共享移动性是指在用户之间共享的传输服务,其中一个核心问题是路线规划。给定一组工人和请求,路线规划为每个工人找到一条路线,即一系列用于接收和放下不时到达的乘客/包裹的位置并具有不同的优化目标。以前的研究缺乏实用性,因为它们的目标相互冲突,并且在将新请求插入路径时效率低下,是一种称为插入的基本操作。在本文中,我们提出了一种称为URPSM的统一路线规划方案。它具有明确定义的参数化目标函数,消除了先前研究中的矛盾目标,并为共享移动性的实现提供了灵活的多目标路径规划。我们证明该问题是NP-hard的,并且以前没有针对URPSM问题及其其他变化提出具有恒定竞争比的多项式时间算法。为此,我们设计了一个有效且高效的解决方案来解决URPSM问题。我们设计了一种新颖的动态规划(DP)算法,以便将插入操作从之前的立方或二次时间加速到仅为线性时间。在DP算法的基础上,我们提出了一种基于贪婪的URPSM问题解决方案。实际数据集上的实验结果表明,我们的解决方案在效率方面优于现有技术1.2至12.8倍,并且运行速度提高了2.6至20.7倍。
1.介绍
共享移动性是指用户共享的运输服务,例如共享汽车,食品配送和众包包裹递送[38]。 共享机动性通过改变路线和利用未充分利用的车辆可减轻污染,降低运输成本,并提供最后一英里交付解决方案[45]。 它被预测为城市交通的有效和可持续的替代方案。
现实共享移动性的关键是工作者和请求之间的路径规划。 工人可以是共享汽车服务的司机或食品和包裹递送服务的快递员,请求包括出发点和目的地及拾取放下信息。 路线规划为每个工人找到一条路线,即一系列位置,用于拾取和放下动态到达的乘客/包裹,具有不同的优化目标。
共享移动的路线规划吸引了来自数据库,数据挖掘和交通科学界的广泛研究兴趣。 大多数研究考虑以下目标中的一个或一个子集:(i)最小化总行程距离[30] [25] [34] [41] [40] [24]; (ii)最大化服务请求的数量[19] [47] [21] [29] [40] [24]; (iii)最大化总收入[13] [14]。 许多解决方案都是启发式的,并且依赖于插入操作,该操作将新请求的原点和目的地插入到当前路径中[30] [25] [41] [34] [19] [47] [40] [18]]。 在实践中,先前的研究具有以下限制。
限制1.现有提案有时会采用多个模糊甚至冲突的优化目标。 例如,在[30] [25] [34] [40] [24]中,目标是最小化请求的总行程距离,但未指定至少提供多少请求。 因此“最佳”解决方案是根本不提供任何请求,这与常识和最大化所服务请求的数量的目标相矛盾。 各种现实世界的共享移动性应用都期望拥有灵活且优化目标一致的统一路由规划问题。
限制2.现有解决方案[30] [25] [47] [18] [31]中的插入操作对于大规模共享移动平台来说效率低下。 将新请求插入路径至少需要平方时间,这使得插入成为在实际应用程序中处理大量请求的瓶颈。
为了解决这些限制,我们定义了一个新问题,共享移动统一路由规划(URPSM)。 它将主流优化目标统一到一个明确定义的目标函数中,其中各个目标是兼容的。 URPSM问题可以灵活地调整特定应用程序的优化目标。 我们发现,上述的三个优化目标可以作为URPSM问题的特殊情况解决。
由于许多路径规划算法的效率瓶颈是插入操作,所以我们设计了一种新的动态规划(DP)算法,将时间复杂度从立方或二次[18] [30] [25] [19] [47]降低到线性。 关键是动态规划可在O(1)时间内找到最佳拾取位置。
此外,与先前忽略分析复杂度不同,我们对URPSM问题进行了系统的理论分析。 我们澄清并证明,没有算法能解决具有URPSM问题的恒定竞争比率问题及其在先前文献中研究的特殊案例[30] [25] [18]。 我们最终为URPSM问题设计了一种有效且高效的启发式解决方案。
我们的主要贡献可归纳如下。
- 我们通过明确定义的参数化目标函数抽象出能解决共享移动性的路径规划问题的统一公式,即URPSM。 它消除了先前研究中的矛盾目标,并可以解决实际共享移动应用中的灵活多目标路线规划。
- 我们设计了一种新颖的动态规划(DP)算法来加速插入操作。 我们的算法将此基本操作的时间复杂度从立方或二次曲线减少到线性。
- 我们全面分析了URPSM问题及其近似问题的难度。 具体来说,我们证明了URPSM问题及其特殊情况不存在具有恒定竞争比的多项式时间算法。 结果可作为分析其他路线规划问题和指南的参考,并可用于设计URPSM问题的有效解决方案。
- 我们使用基于DP的插入来设计有效且高效的解决方案,以解决URPSM问题。
- 对真实数据集的广泛实验表明,我们的解决方案比现有技术的速度快2.6到20.7倍,效率提高1.2到12.8倍[25] [11]。
在本文的其余部分,我们在第2节中回顾相关工作,在第3节中定义URPSM问题并讨论其广泛性和难度。在第4节中提出了基于动态规划的插入操作。在第5节中设计了URPSM问题的完整解决方案。 最后,我们在第6节中评估,在第7节中总结。
2.相关工作
关于共享移动性(RPSM)的路径规划的研究可以追溯到1975年提出的拨号问题[43] [44],并且已经由数据库,数据挖掘,运输科学社区进行了研究。 本节简要回顾了RPSM问题的不同变体及其解决方案。
RPSM问题的一个重要设置是静态还是动态。 在静态(离线)RPSM问题中,工作人员和请求的信息是事先已知的。 相反,在动态(在线)设置中,工作人员或请求会动态显示,并且需要在短时间内甚至立即提供请求。 动态RPSM问题更符合现实世界的共享移动应用的需求[30] [25] [41] [34] [47] [19] [13] [14],并将成为我们的主要关注点。
RPSM问题的主流目标包括最小化总旅行距离[16] [23],最大化服务请求的数量[29] [47] [19] [40],最大化总收入[13] [14]等。 总行程距离是计算工人因请求行走的总行程距离。较小的总行程距离表明行程成本低,污染小[10]。大量服务请求可提高共享移动提供商的收入[47]。 更常见的目标是在提供所有请求时最小化总行程距离[30] [25] [41] [34]。 其他研究的重点是最大化共享移动提供商的总收入(服务请求的总支付额减去工人的总工资)[13] [14],最小化完工时间(最后一次请求的完成时间)[12] [22],或最大化工人和请求之间复杂的社会效用[18]。 我们的目标是分析主流目标之间的关系,并将它们整合到一个兼容和灵活的表述中。
目前已经提出了许多动态RPSM问题的解决方案[30] [25] [41] [34] [47] [19],其中一种称为插入的核心操作被广泛使用。 郑等人 [30] [41]使用枚举策略搜索最佳插入位置,该位置需要满足插入请求的约束。 由于对请求数量的额外限制,可以进一步减少可行插入,但也可能错误地删除最佳插入[34] [37]。 并行性也可于加速插入[34]。 插入经常用于解决大规模动态RPSM问题。 然而,插入具有二次或甚至三次时间复杂度,这是效率的瓶颈。 这促使我们设计线性插入算法。
为了解决动态RPSM问题,郑等人 [30] [41]首先通过网格索引搜索一组候选工作者,然后以最小的增加距离将请求插入候选人。 黄等人[25]提出了动态数据结构来存储所有可能的路线,并使用类似的插入程序来最小化总行程距离。AlonsoMora等[11]采用基于批处理的方法首先将一些请求分成小组,然后将一组请求插入到一个工作者的路径中。 但是,这些研究不适合大规模共享移动应用。 在新的线性插入操作的基础上,我们提出了一个完整的RPSM问题的启发式解决方案,这比这些研究都更有效和高效。
3.问题陈述
本节定义了URPSM问题,该问题统一了先前研究的目标函数[30] [25] [34] [41] [47] [21] [29] [40] [24] [13] [14]。
3.1符号和定义
定义1 (路网)。一个路网由一个无向图 G = ( V , E ) G=(V,E) G=(V,E)表示,其中 V V V表示点的集合, E E E表示点的集合。每个边 ( u , v ) ∈ E (u,v)\in E (u,v)∈E都和旅行成本 ( u , v ) (u,v) (u,v)相关联。
旅行成本可以是距离或平均旅行时间,这个成本可以从OpenStreetMap [6]或大型历史轨迹挖掘[48]获得。 我们在本文中将交替使用旅行时间和旅行距离。 我们将 d i s ( u , v ) dis(u,v) dis(u,v)表示为任意两个顶点 u ∈ V u\in V u∈V和 v ∈ V v∈V v∈V之间的最短路径的距离。
定义2 (工人)。工人用 w = < o w , K w > w = <ow,Kw> w=<ow,Kw>表示, o w ∈ V ow∈V ow∈V表示初始位置, K w Kw Kw表示容量。
工人的容量是出租车可以乘坐的最大乘客数量或者快递箱可以随时包含的最大数量。 我们使用 W = { w 1 … w W } W = \lbrace w_1\ldots w_ W \rbrace W={w1…wW}来表示所有工人。
定义3 (请求)。请求由 r = < o r , d r , t r , e r , p r , K r > r=<o_r,d_r,t_r,e_r,p_r,K_r> r=<or,dr,tr,er,pr,Kr>表示,其中原点 o r ∈ V o_r∈V or∈V,目的地 d r ∈ V d_r∈V dr∈V , K r K_r Kr表示容量。它是在共享移动平台(简称平台)上发布的, t r t_r tr表示发布时间, e r e_r er表示截止日期,请求需要在这之前送达。如果 ( i ) (i) (i)工人在原点拾取r的时间超过 t r t_r tr; ( i i ) (ii) (ii)同一工人在 e r e_r er前将r送至 d r d_r dr处,则请求被送达。如果请求未被送达(或被拒绝拒绝),平台将受到处罚 p r p_r pr。
请求的容量Kr指定在一次请求中共乘的乘客人数或快递服务中的项目数。需要注意的是,在实际应用中可以有两个截止日期,即收件和交付的截止日期。然而,送货的单一期限通常就足够了,因为收件的最后期限可以表示为 e r − d i s ( o r , d r ) e_r−dis(o_r, d_r) er−dis(or,dr)。如果有一个紧迫的截止日期,很难满足每个请求(例如,5到6分钟的共乘时间[30][13])。那么平台可以拒绝某些请求,这会导致损失,即罚款 p r p_r pr,这是从服务请求或用户体验中损失的收入。处罚是针对具体应用的。我们使用 R = { r 1 … r ∣ R ∣ } R= \lbrace r_1 \ldots r_ {\mid R \mid }\rbrace R={r1…r∣R∣}表示所有请求,使用 R w R_w Rw表示工作人员 w w w所服务的所有请求。我们进一步将 R + = ⋃ w ∈ W R w R^+= \bigcup _{w \in W} R_w R+=⋃w∈WRw表示为所有服务请求,并将 R − = R − R + R^−=R−R^+ R−=R−R+表示为所有被拒绝的请求。
定义4 (路线)。工人的路线定义为 S w = ⟨ o w , l w 1 , … , l w ∣ S w ∣ − 1 ⟩ S_w = \langle o_w,l^1_w, \ldots ,l_w^{\mid S_w\mid-1 }\rangle Sw=⟨ow,lw1,…,lw∣Sw∣−1⟩,其中 ⟨ l w 1 , … , l w ∣ S w ∣ − 1 ⟩ \langle l^1_w, \ldots ,l_w^{\mid S_w\mid-1} \rangle ⟨lw1,…,lw∣Sw∣−1⟩是 R w R_w Rw的一个有序的原点和目的序列,即 l w i ∈ { o r ∣ r ∈ R w } ⋃ { d r ∣ r ∈ R w } l^i_w \in \lbrace o_r \mid r \in R_w \rbrace \bigcup \lbrace d_r \mid r \in R_w \rbrace lwi∈{or∣r∈Rw}⋃{dr∣r∈Rw}。如果 ( i ) ∀ r ∈ R w (i)\forall r \in R_w (i)∀r∈Rw, o r o_r or和 d r d_r dr在序列中存在并且 o r o_r or在 d r d_r dr之前; ( i i ) ∀ r ∈ R w (ii) \forall r \in R_w (ii)∀r∈Rw, w w w到达时间目的地的时间不超过最迟期限; ( i i i ) (iii) (iii)在任何时间,在这条路线上被接载但未交付的乘客/物品的数目,不超过该工人的运载容量,则路径是可行的。
我们用 D ( S w ) D(S_w) D(Sw)来表示 S w S_w Sw的总行程,其中
![]()
3.2 统一目标与URPSM问题
定义5 (URPSM)。给定一个公路网,一组工人 W W W,一组只有在他们被释放时才知道的请求和一个权重系数 α α α,URPSM问题是为每个工人寻找一条 S w S_w Sw路线,使统一成本 U C ( W , R ) UC(W,R) UC(W,R)最小化。
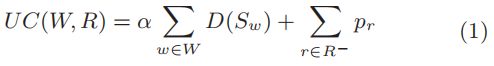
并且满足下述限制: ( i ) (i) (i)可行性限制:每个工人都被安排一条可行路线; ( i i ) (ii) (ii)恒定限制:一旦请求被拒绝,它们就不能被撤销。否则,他们必须得到服务。
我们用下面的例子来说明URPSM问题。
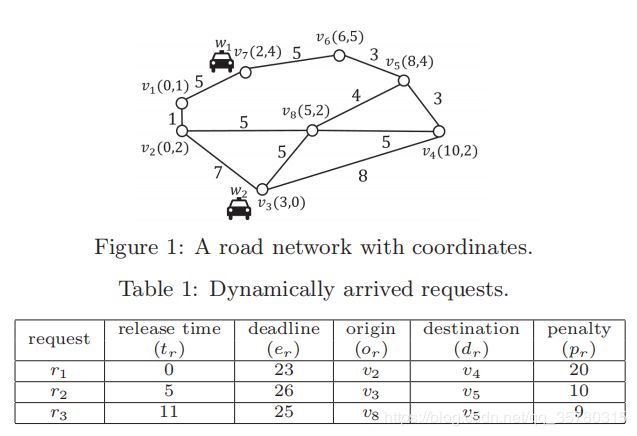
例1. 假设一个包含两个工人(车辆) w 1 、 w 2 w1、w2 w1、w2和三个动态到达请求 r 1 − r 3 r1-r3 r1−r3的共享平台。工人的初始位置被标记在有8个顶点 v 1 − V 8 v1-V8 v1−V8的道路网络上,如图1所示。顶点的坐标(纬度和经度)也有标记。例如, v 1 v1 v1的坐标是(0,1)。表1列出了请求的细节。我们假定 α = 1 , K w 1 = K w 2 = 4 , K r 1 = K r 2 = K r 3 = 1 α=1,K_{w1}=K_{w2}=4,K_{r1}=K_{r2}=K_{r3}=1 α=1,Kw1=Kw2=4,Kr1=Kr2=Kr3=1。
在时间 0 ( T r 1 ) 0(T_r1) 0(Tr1),请求 r 1 r_1 r1被释放,原点在 v 2 v_2 v2,目的地在 v 4 v_4 v4。为了服务 r 1 r_1 r1,平台需要计划一条路线,在 v 2 v_2 v2接收 r 1 r_1 r1,并在最后期限23之前在 v 4 v_4 v4交付。一个可行的路线是 ⟨ o w 1 , v 2 , v 4 ⟩ \langle o_w1,v_2,v_4\rangle ⟨ow1,v2,v4⟩,在时间为5+1+5+5=16时到达 v 4 v_4 v4。具体来说, w 1 w_1 w1从 v 7 v_7 v7开始,第一次从 v 1 v_1 v1旅行到 v 2 v_2 v2。 w 1 w_1 w1在 v 2 v_2 v2处取 r 1 r_1 r1,然后从 v 8 v_8 v8到 v 4 v_4 v4。最后, w 1 w_1 w1在最后期限 e r 1 = 23 er_1=23 er1=23之前将 r 1 r_1 r1带到目的地。平台还可以拒绝请求,这将导致处罚 p r 1 = 20 p_r1=20 pr1=20。URPSM问题为每个工人规划了路线,并将统一成本降到最低,这包括总行程和对未得到服务的请求的惩罚。
接下来,我们证明了以前的许多研究都是具有特定 α α α和 p r p_r pr设置的URPSM问题的特例。
- 最小化总行程[25][41][30][33][35].通过设置 α = 1 α=1 α=1和 ∀ r ∈ R , p r = ∞ ∀r∈R,p_r=∞ ∀r∈R,pr=∞,最小化 E q . ( 1 ) Eq.(1) Eq.(1)相等于在处理所有请求时尽量减少总旅行距离。
- 最大化已送达请求的数量[47][19][29][21]。通过设置 α = 0 α=0 α=0和 ∀ r ∈ R , p r = 1 ∀r∈R,p_r=1 ∀r∈R,pr=1,最小化 E q . ( 1 ) Eq.(1) Eq.(1)等于尽量减少未送达请求的数目(即最大限度地增加已送达请求的数量),假设任何r的惩罚为pr=1。
- 最大限度地增加总收入[13][14]。平台的总收入包括工人的收入和服务请求的费用。工人的收入与总工作时间(或旅行距离)和单位时间 c w cw cw的收入有关。服务请求的费用与旅行距离和单位距离 c r cr cr的费用相关。然后计算平台的总收入如下:
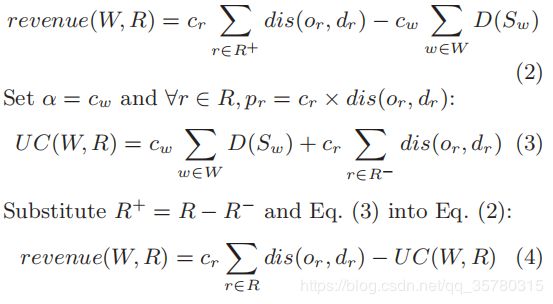
由于请求是给定的(即第一个项是常数),最小化 U C ( W , R ) UC(W,R) UC(W,R)就等于使总收入最大化。
3.3 难度分析
本节分析了URPSM问题及其变体的竞争难度。URPSM问题是NP-hard问题,因为它推广了现有的NP-hard问题[30].然而,对竞争难度的研究却很少。唯一已知的结果[13]证明了不存在确定性算法可以保证总收益最大化的恒竞争比,但其结论是否适用于随机算法尚不清楚。我们通过研究随机算法是否能保证对不引人注意的对手保持恒定的竞争比来分析竞争的难度[15]。如果不存在这样的随机算法,那么任何确定性算法也不会存在[15]。
定理1给出了我们的主要结论。
定理1. 下列URPSM问题的特殊情况对于任意一个随机问题都没有恒定的竞争比。
(1)最大限度地利用服务请求数,即 α = 0 α=0 α=0和 ∀ r ∈ R , p r = 1 ∀r∈R,p_r=1 ∀r∈R,pr=1;
(2)最大限度地提高平台的总收入,即 α = c w α=cw α=cw和 ∀ r ∈ R , p r = c r × d i s ( o r , d r ) ∀r∈R,p_r=cr×dis(o_r,d_r) ∀r∈R,pr=cr×dis(or,dr);
(3)最小化服务所有请求时的总距离,即 α = 1 α=1 α=1和 p r = ∞ p_r=∞ pr=∞。
我们分别用引理1、引理2和引理3依次证明了定理1中的三种陈述。、
引理1. 当 α = 0 , ∀ r ∈ R , p r = 1 α=0,∀r∈R,p_r=1 α=0,∀r∈R,pr=1时,随机算法和确定性算法都不具有恒定的竞争比。
证明. 我们只需证明任何随机算法都不能保证恒竞争比。我们首先生成输入的分布,并证明任何确定性算法在这个输入上的期望值不是常数(例如, ∞ ∞ ∞)。然后,应用姚的原理[46],没有随机算法有一个恒定的竞争比。
请求、工人和路网的生成的分布如下所示: ( i ) (i) (i)假设道路网 G G G是一个无向环图,其维数为0,且每条边的长度为1。 ( i i ) (ii) (ii)我们假定一个工人的初始位置为 o w = v 1 o_w=v_1 ow=v1,容量 k w = 2 k_w=2 kw=2。 ( i i i ) (iii) (iii)请求 r r r在时间 t r = ∣ V ∣ t_r = \mid V \mid tr=∣V∣上被释放,其原点 o r o_r or一致从所有顶点的集合 V V V中随机生成。设 d r = o r , e r = t r + ϵ , ϵ > 0 , p r = K r = 1 d_r=o_r,e_r=t_r+\epsilon,\epsilon>0,p_r=K_r=1 dr=or,er=tr+ϵ,ϵ>0,pr=Kr=1。
由于请求是在时间 ∣ V ∣ \mid V \mid ∣V∣上释放的,并且图中有 ∣ v ∣ \mid v\mid ∣v∣的顶点,所以在最优解中的工作人员有足够的时间(即, ∣ V ∣ \mid V\mid ∣V∣)来到达或释放请求 r r r。因此, r r r总是可以有最优解的,而未处理请求的期望数为零,即 E χ [ O P T ] = 0 Eχ[OPT]=0 Eχ[OPT]=0。
考虑一个通用的确定性在线算法ALG,当 r r r被释放时,它的工作人员位于点(不是顶点) u u u。只要 u u u和 o r o_r or之间的最短距离不大于 ϵ \epsilon ϵ,ALG就能以概率 ≤ 2 ϵ ∣ V ∣ ≤\frac{2\epsilon}{\mid V\mid} ≤∣V∣2ϵ的形式服务 r r r。由于只有一个请求,所以ALG未处理请求的预期数量是 E χ [ A L G ] ≥ 1 − ≤ 2 ϵ ∣ V ∣ Eχ[ALG]≥1−≤\frac{2\epsilon}{\mid V\mid} Eχ[ALG]≥1−≤∣V∣2ϵ。因此
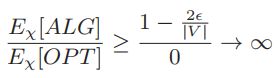
上述比率无界。
引理2. 当 α = c w , ∀ r ∈ R , p r = c r × d i s ( o r , d r ) α=c_w,∀r∈R,p_r=c_r\times dis(o_r,d_r) α=cw,∀r∈R,pr=cr×dis(or,dr)时,随机算法和确定性算法都不具有恒定的竞争比。
证明. 我们通过调整引理1的证明中分布的设置来证明引理2。具体来说,我们为请求 r r r生成分布 d r d_r dr,如下所示。 d r d_r dr总是从圈图中的一个顶点集中选择,其距离到 o r o_r or的距离为 ∣ V ∣ / 2 \mid V\mid/2 ∣V∣/2。因为在无向循环图上,与工人位置和 o r o_r or的距离不大于 ∣ V ∣ / 2 \mid V\mid/2 ∣V∣/2,并且 d i s ( o r , d r ) = ∣ V ∣ / 2 dis(o_r,d_r)=\mid V\mid/2 dis(or,dr)=∣V∣/2,工人将移动另一个 ∣ V ∣ / 2 \mid V\mid/2 ∣V∣/2来服务 r r r。因此,工人的总行程距离不超过 ∣ V ∣ / 2 + ∣ V ∣ / 2 = ∣ V ∣ \mid V\mid/2 +\mid V\mid/2=\mid V\mid ∣V∣/2+∣V∣/2=∣V∣。我们还假定有足够大的 c r c_r cr,例如 c r > 2 c w c_r>2c_w cr>2cw,否则当工人的总距离接近于 ∣ V ∣ \mid V\mid ∣V∣时,最优解可能会拒绝r。那我们就有了
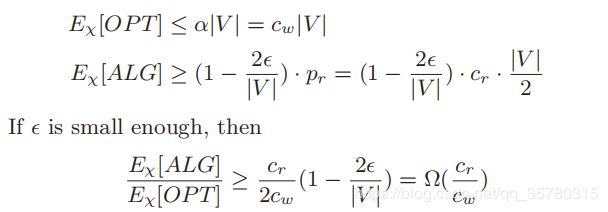
因此,无论是随机算法还是确定性算法都没有恒定的竞争比。
引理3. 当 α = 1 , p r = ∞ α=1,p_r=\infty α=1,pr=∞时,随机算法和确定性算法都不具有恒定的竞争比。
证明. 我们利用引理1的证明中的分布证明引理3。根据前面的分析,在这种分布下,最优路径的总距离是有界的,为 ∣ V ∣ \mid V \mid ∣V∣,任意的确定性算法都有 1 − ≤ 2 ϵ ∣ V ∣ 1−≤\frac{2\epsilon}{\mid V\mid} 1−≤∣V∣2ϵ拒绝r的概率。因此,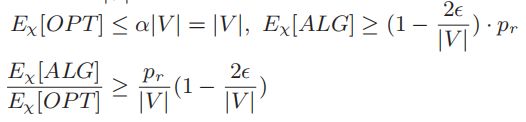
通过设置足够小的 ϵ \epsilon ϵ , p r = ∞ p_r = \infty pr=∞,上述比率无界。
![]()
4.基于DP的插入
虽然对于URPSM问题,目前还没有一种有效的解决算法(SEC.3.3),以插入为基础的解决办法对URPSM问题[30][25][41][34]的变体实际上是有效的。然而,在大规模动态共享移动应用中,插入操作也是一个效率瓶颈。本节对插入操作进行了形式化定义,并提出了一种新的基于dp的算法,以提高算法的效率。
4.1准备工作
插入最早是在[32]中提出的,用于车辆路径问题(VRP)[20],该问题为一组车辆安排最佳路线,以便将给定的一组请求(乘客)发送到不同的城市。基于插入的解决方案的思想是通过一次插入一个顶点(城市)来迭代地排列车辆的路径。这一思想可以通过一次插入两个顶点(即请求的起源和目的地)来扩展,并已被用于设计拨号-a-平顺问题及其变体[27][28][36][26]的启发式解。虽然该插入是为单个工作人员的路由规划提出的,但它也被广泛地应用于多工人路线规划中,其中基于插入的路由规划是针对每个工人单独执行的[18][30][25]。
形式上,我们在[27][28]中的约定之后定义插入操作如下。
定义6 (插入)。给出了一个由n个顶点组成的新请求r和一个由n个顶点组成的新路由w,该插入操作的目的是通过将 o r , d r o_r,d_r or,dr插入到 S w S_w Sw中,从而使在 S ∗ S^∗ S∗中的顶点顺序保持不变,找到一个新的可行路由 S ∗ S^∗ S∗,以最小的增加距离来进一步服务r。
通过插入一对起点和目的地的最小增加距离,它也最小化了总旅行距离。因此,该目标与我们的URPSM问题一致,该问题将加权总距离和未服务请求的惩罚最小化。本文首先回顾了文献[27]中提出的基本插入,然后设计了一种具有二次时间复杂度和线性记忆复杂度的朴素的基于DP的插入,并设计了具有线性时间复杂度和记忆复杂性的改进版本。
4.2 基本插入

在[27][28]中提出了基本插入,但没有对效率进行优化。它的思想是: ( 1 ) (1) (1)列举所有 o r o_r or和 d r d_r dr可能的插入位置(例如 ( i , j ) ) (i,j)) (i,j)),以获得新的路由 S w ′ S_w^ {'} Sw′; ( 2 ) (2) (2)检查新路由 S w ′ S_w^ {'} Sw′是否违反任何约束; ( 3 ) (3) (3)如果不违反约束且 S w ′ S_w^ {'} Sw′增加较短的距离,则用 S w ′ S_w^ {'} Sw′替换 S ∗ S^∗ S∗。
算法1.

说明基本插入。在第1行中,在没有可行路由的情况下,将一个新的路由 S ∗ S^∗ S∗初始化为 S w S_w Sw。在第2-3行中,我们列举了所有可能的拾取地点(在 S w S_w Sw的 i − t h i-th i−th)和交付的位置(在 S w S_w Sw的 j − t h j-th j−th)。在第4-7行中,我们生成一个新的路由 S w ′ S_w^{'} Sw′,并检查它是否可行.如果是,我们计算它的增加距离 Δ i , j Δ_{i,j} Δi,j,并将其与当前最小 Δ ∗ Δ^∗ Δ∗进行比较。如果 Δ i , j < Δ ∗ Δ_{i,j}<Δ^∗ Δi,j<Δ∗ , 我们使用 S w ′ S_w^{'} Sw′更新 S ∗ S^∗ S∗,使用 Δ i , j Δ_{i,j} Δi,j更新 Δ ∗ Δ^∗ Δ∗。
复杂度分析. 在第2-3行中,可能的 ( i , j ) (i,j) (i,j)对数是 O ( n 2 ) O(n^2) O(n2)。第5行检查新路由 S w ′ S_w^{'} Sw′是否违反了 O ( n ) O(n) O(n)时间内的容量和截止日期限制。如果没有,则需要 O ( n ) O(n) O(n)时间来计算第6行中增加的距离。第5-6行涉及最短距离查询。上述分析假设一个最短距离查询需要 O ( 1 ) O(1) O(1)时间,就像许多以前的研究[11][13][18][33]一样。这一假设是合理的,因为像滴滴[3]这样的现实世界中的共享移动公司将最短距离查询视为恒定时间的基本操作。除非明确规定,否则我们将在本文其余部分采用这一假设。第5-7行检查 S w ′ S_w^{'} Sw′并更新 S ∗ S^∗ S∗和 Δ ∗ Δ^∗ Δ∗,这也需要 O ( n ) O(n) O(n)时间.因此,基本插入的总时间成本为 O ( n 3 ) O(n^3) O(n3),总内存成本为 O ( n ) O(n) O(n)。如果最短距离查询需要 O ( q ) O(q) O(q)时间,则算法需要 O ( n 3 q ) O(n^3q) O(n3q)时间。
4.3 基于朴素DP的插入
该部分提出了一种朴素的基于DP的插入算法,将基本插入的 O ( n 3 ) O(n^3) O(n3)时间复杂度降低到 O ( n 2 ) O(n^2) O(n2)。其思想是 ( 1 ) (1) (1)列举所有 o r o_r or和 d r d_r dr可能的插入位置, ( 2 ) (2) (2)检查一条新路径是否可行,并在 O ( 1 ) O(1) O(1)时间内计算 Δ i , j Δ_{i,j} Δi,j,而不是在基本插入中计算 O ( n ) O(n) O(n)时间。我们首先解释了如何计算 Δ i , j Δ_{i,j} Δi,j,因为它将用于检查新路线的可行性。
4.3.1 在 O ( 1 ) O(1) O(1)时间内计算 Δ i , j \Delta_{i,j} Δi,j
与其从零开始计算 Δ i , j = D ( S w ′ ) − D ( S w ) Δ_{i,j}=D(S_w^{'})−D(S_w) Δi,j=D(Sw′)−D(Sw),这需要 O ( n ) O(n) O(n)时间,不如在 O ( 1 ) O(1) O(1)时间内计算 Δ i , j Δ_{i,j} Δi,j时,这需要在 l i l_i li和 l k l_k lk之间插入 l j l_j lj时利用绕行。具体来说,弯道 d e t ( l i , l j , l k ) det(l_i,l_j,l_k) det(li,lj,lk)的定义如下。
![]()
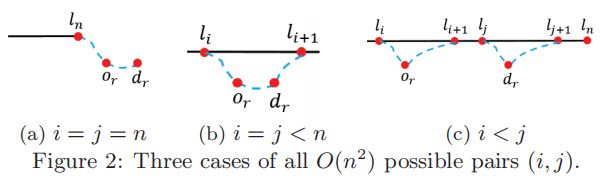
它是当 l j l_j lj插入 l i l_i li和 l k l_k lk之间时增加的距离。因此,可以用图2中的绕行在 O ( 1 ) O(1) O(1)时间内计算Δ_{i,j}$,其中图 2 a 2a 2a和图 2 b 2b 2b是 i = j i=j i=j时的两个特例,而图 2 c 2c 2c是一般情况。
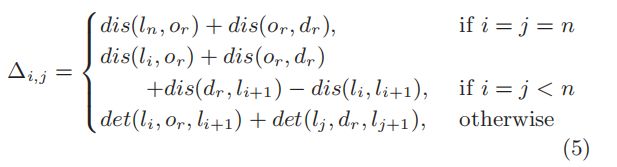
4.3.2 在 O ( 1 ) O(1) O(1)时间内检查路线可行性
为了检验一条新路线是否可行,我们应该检查 ( i ) (i) (i)最后期限约束和 ( i i ) (ii) (ii)定义4中定义的容量约束。
为了检验 O ( 1 ) O(1) O(1)时间中的最后期限约束,我们借用了松弛时间[27]的概念。将 d d l [ k ] ddl[k] ddl[k]表示为在不违反任何截止日期限制的情况下到达 l k l_k lk的最新时间。如果 l k l_k lk是 r r r的起源,我们将 d d l [ k ] ddl[k] ddl[k]设为 e r − d i s ( o r , d r ) e_r−dis(o_r,d_r) er−dis(or,dr),如果 l k l_k lk是 r r r的目的地,则设 e r e_r er。
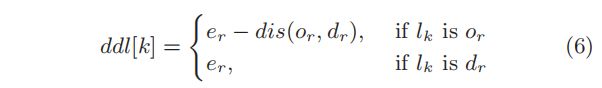
将 a r r [ k ] arr[k] arr[k]表示为 w w w到达 l k l_k lk的时间。
![]()
进一步将 s l a c k [ k ] slack[k] slack[k]表示为 l k l_k lk和 l k + 1 l_{k+1} lk+1之间为满足 l k l_k lk后所有最后期限的最大容许时间(即松弛时间)。由于 l k l_k lk后的绕行可能导致工人违反 l k + 1 , ⋅ ⋅ , l n l_{k+1},··,l_n lk+1,⋅⋅,ln, s l a c k [ k ] slack[k] slack[k]的最后期限,不应超过位置 l k + 1 ( d d l [ k + 1 ] − a r r [ k + 1 ] ) l_{k+1}(ddl[k+1]−arr[k+1]) lk+1(ddl[k+1]−arr[k+1])和位置 l k + 1 ( s l a c k [ k + 1 ] ) l_{k+1}(slack[k+1]) lk+1(slack[k+1])的最后期限。因此, s l a c k [ ⋅ ] slack[·] slack[⋅]可以按以下方式计算。
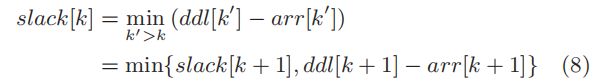
引理4. 当且仅当(1) a r r [ i ] + d i s ( l i , o r ) ≤ e r arr[i]+dis(l_i,o_r)≤e_r arr[i]+dis(li,or)≤er;(2) d e t ( l i , o r , l i + 1 ) ≤ s l a c k [ i ] det(l_i,o_r,l_{i+1})≤slack[i] det(li,or,li+1)≤slack[i]时,;(3)当 i = j ( 图 2 A 和 图 2 B ) i=j(图2A和图2B) i=j(图2A和图2B)时, a r r [ i ] + d i s ( l i , o r ) + d i s ( o r , d r ) ≤ e r arr[i]+dis(l_i,o_r)+dis(o_r,d_r)≤e_r arr[i]+dis(li,or)+dis(or,dr)≤er, 当 i < j i<j i<j(图 2 c 2c 2c)时, a r r [ j ] + d e t ( l i , o r , l i + 1 ) + d i s ( l j , d r ) ≤ e r arr[j]+det(l_i,o_r,l_{i+1})+dis(l_j,d_r)≤e_r arr[j]+det(li,or,li+1)+dis(lj,dr)≤er;(4) Δ i , j ≤ s l a c k [ j ] Δ_{i,j}≤slack[j] Δi,j≤slack[j]时才不会违反最后期限约束。
证明(草图). 如果 o r o_r or插入到第 i i i次 , 条件(1)检查是否违反了新请求 r r r的截止日期约束;如果 o r o_r or插入到第 i i i次 , 条件(2)检查是否违反了所有其他请求的任何最后期限约束。类似地,条件(3)检查如果在 j − t h j-th j−th时插入 d r d_r dr,是否违反了 r r r的最后期限约束;条件(4)检查如果在 j − t h j-th j−th时插入 d r d_r dr,是否违反了所有其他请求的任何最后期限约束。有关更多细节,我们请读者参阅[42]。
为了在 O ( 1 ) O(1) O(1)时间内的检查容量约束,我们使用选中的请求(即 p i c k e d [ k ] picked[k] picked[k])来表示当前收到但尚未交付的请求的数量。那我们就有了
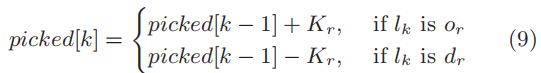
引理5. 当且仅当(1) p i c k e d [ i ] ≤ K w − K r picked[i]≤K_w−K _r picked[i]≤Kw−Kr和(2) ∀ k , i < k ≤ j , p i c k e d [ k ] ≤ K w − K r ∀k,i<k≤j,picked[k]≤K_w−K_r ∀k,i<k≤j,picked[k]≤Kw−Kr时,工人 w w w的容量约束不会被违反。
证明. 当 o r o_r or插入在 i − t h i-th i−th时, p i c k e d [ i ] picked[i] picked[i]不应大于 K w − K r K_w−K_r Kw−Kr . 我们还需要检查是否存在任何整数 k ∈ ( i , j ) k∈(i,j) k∈(i,j), p i c k e d [ k ] picked[k] picked[k]大于 K w − K r K_w−K_r Kw−Kr。由于请求 r r r是在 l j l_j lj之后立即传递的,如果 p i c k e d [ k ] > k w − k r picked[k]>k_w−k_r picked[k]>kw−kr,这将超过 l k l_k lk的工人容量 K w K_w Kw,这违反了 w w w的容量约束。
4.3.3 算法草图

算法2. 显示带有初始化的朴素DP插入,并在第2行中通过公式6-公式9进行初始化。第9行由公式5计算。第4行、第6行和第10行实现引理4。第5行和第8行实现引理5。
复杂度分析. 第2行需要 O ( n ) O(n) O(n)时间来初始化 a r r , d d l , s l a c k , p i c k e d arr , ddl , slack , picked arr,ddl,slack,picked。第12行需要 O ( n ) O(n) O(n)时间,在第3-11行中还有 O ( n 2 ) O(n^2) O(n2)迭代。其他行都需要 O ( 1 ) O(1) O(1)时间。总时间成本为 O ( n 2 ) O(n^2) O(n2),总内存成本为 O ( n ) O(n) O(n)。如果最短距离查询需要 O ( q ) O(q) O(q)时间,则算法需要 O ( n 2 q ) O(n^2q) O(n2q)时间。
4.4 线性基于DP的插入
本节提出了一种改进的基于DP的线性时间复杂度插入(简称线性DP插入)。它在不列举所有可能的插入位置(i,j)的情况下,以最小的增加距离找到路径。线性DP插入是建立在朴素DP插入的基础上的,但它利用了两个洞察力。 ( i ) (i) (i)如图2A及图2B所示,当i=j时,只需 O ( n ) O(n) O(n)时间为特殊情况寻找最佳路线。 ( i i ) (ii) (ii)给定一个固定的 j j j,则一般情况下只需 O ( 1 ) O(1) O(1)时间通过动态规划找到最佳 i i i,如图2C所示。第一个洞察力是微不足道的,因为检验 S w ′ S_w^{'} Sw′的可行性和计算 Δ ∗ Δ^∗ Δ∗需要 O ( 1 ) O(1) O(1)时间。因此,当 i = j i=j i=j时,需要 O ( n ) O(n) O(n)时间来寻找可行的路径,且增加的距离最小。在下面,我们主要解释了第二个洞察力。
4.4.1 列举交付地点
线性DP插入不是枚举所有可能的 ( i , j ) (i,j) (i,j)对,而是只枚举传递位置 ( j ) (j) (j),以找到最佳路由。将 Δ j ∗ Δ^∗_j Δj∗表示为给定j的最小增加距离。对于图2C中的一般情况,
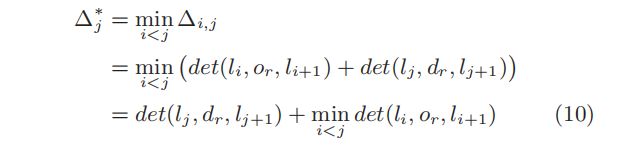
第一个项是插入 j j j后的绕行,对于固定的j是常数。第二项是所有 i < j i<j i<j之间的最小绕行。线性DP插入的关键是找到一个可行的 i i i,使O(1)时间内的第二项最小化。
4.4.2 在 O ( 1 ) O(1) O(1)时间找到最佳拾取位置
我们引入 D i o [ j ] Dio[j] Dio[j]来保持给定 j j j的插入或 i < j i<j i<j之间的最小绕行。即, D i o [ j ] = m i n i < j d e t ( l i , o r , l i + 1 ) Dio[j]=min_ {i<j} det(l_i,o_r,l_{i+1}) Dio[j]=mini<jdet(li,or,li+1)。 D i o [ j ] Dio[j] Dio[j]可通过以下DP公式计算。
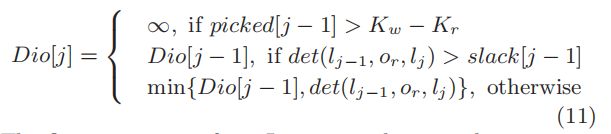
第一种情况来自引理5,第二种情况来自引理4,第三种情况由它的定义给出。
同样的,我们使用 P l c [ j ] Plc[j] Plc[j]记录 o r o_r or对应于 D i o [ j ] Dio[j] Dio[j]的插入位置。
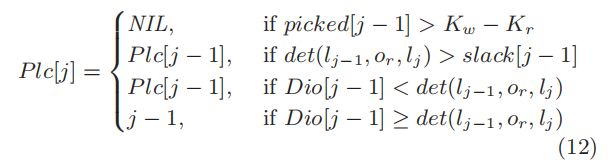
如果 P l c [ j ] Plc[j] Plc[j]和 j j j满足容量约束和最后期限约束,则得到了固定 j j j的最佳可行路径。但是,如果Plc[j]违反了某些约束,则不知道是否有特定的 i ≠ P l c [ j ] i \neq Plc[j] i̸=Plc[j]产生可行的路由。我们通过下面的引理来解决这个问题。
引理6. 如果 P l c [ j ] Plc[j] Plc[j]违反约束,那么其他 i ≠ P l c [ j ] i \neq Plc[j] i̸=Plc[j]也违反约束。
证明. 首先,假设 P l c [ j ] Plc[j] Plc[j]违反容量约束(等式12的第一个条件),根据引理5,任何 i ≤ j − 1 i≤j−1 i≤j−1也将违反容量约束。接下来,假设Plc[j]违反最后期限约束(等式12的第二个条件),假设相反,存在 i ′ < j i^{'}<j i′<j,它满足所有约束。那我们就有了
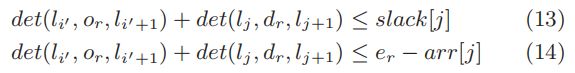
根据等式11,Plc[j]只能与给定的j一起违反最后期限约束,即 d e t ( l i , o r , l i + 1 ) ≤ D i o [ j ] det(l_i,o_r,l_i +1) ≤ Dio[j] det(li,or,li+1)≤Dio[j]。指出 P l c [ j ] Plc[j] Plc[j]也应满足最后期限约束,这与假设相矛盾。
因此,给定一个固定的j,我们可以检查是否存在可以插入 o r o_r or的 i ( < j ) i(<j) i(<j)位置如下所示。
推论1.给定一个固定的j,存在一个可行的插入 o r o_r or充要条件是:(1) p i c k e d [ j ] ≤ K w − K r picked[j]≤K_w−K_r picked[j]≤Kw−Kr,(2) a r r [ j ] + D i o [ j ] + d i s ( l j , d r ) ≤ e r arr[j]+Dio[j]+dis(l_j,d_r)≤e_r arr[j]+Dio[j]+dis(lj,dr)≤er和(3) D i o [ j ] + d e t ( l j , d r , l j + 1 ) ≤ s l a c k [ j ] Dio[j]+det(l_j,d_r,l_{j+1})≤slack[j] Dio[j]+det(lj,dr,lj+1)≤slack[j]。
4.4.3 算法草图

算法3. 说明了线性DP插入的过程。在第4行中,我们使用与算法2相同的方式处理i=j时的情况。在第5-7行中,我们首先通过推论1检查给定的 j j j是否存在一个可行的 i i i。如果是,我们计算了最小增加距离 Δ j ∗ Δ^∗_j Δj∗及其相应的 i ( 即 P l c [ j ] ) i(即Plc[j]) i(即Plc[j])。在第8行中,我们根据引理4剪枝,动态更新 D i o [ j + 1 ] Dio[j+1] Dio[j+1]和 P l c [ j + 1 ] Plc[j+1] Plc[j+1]。

例2. 返回到示例1中的设置。假设 w 1 w_1 w1被分配给遵循 S w 1 = ⟨ w 1 , v 2 , v 4 ⟩ S_{w1}=\langle w_1,v_2,v_4\rangle Sw1=⟨w1,v2,v4⟩路由的 r 1 r1 r1。当 r 2 r2 r2在第5时间释放时, w 1 w_1 w1在 v 1 v_1 v1。因此,除了 w 1 w_1 w1的当前位置外, S w 1 S_{w1} Sw1中还有另一个 n = 2 n=2 n=2个顶点。如果在当前路由 S w 1 S_{w1} Sw1中插入 r 2 r2 r2,则算法3第2行中的数组被初始化,如表3所示。 d d l [ 0 ] = ∞ ddl[0]=∞ ddl[0]=∞,因为 l 0 = v 1 l_0 = v_1 l0=v1既不是 r 1 r_1 r1的起源也不是目的地。当前时间为5, a r r [ 0 ] = 5 arr[0]=5 arr[0]=5。 p i c k e d [ 0 ] = 0 picked[0]=0 picked[0]=0,因为 w 1 w_1 w1没有接收任何请求。当 k > 0 k>0 k>0时,用等式6、7和9初始化 d d l [ k ] , a r r [ k ] , p i c k e d [ k ] ddl[k],arr[k],picked[k] ddl[k],arr[k],picked[k]。具体来说,当 l 1 = v 2 l_1=v_2 l1=v2是 o r o_r or并且 l 2 = v 4 l_2=v_4 l2=v4是 d r d_r dr时, d d l [ 1 ] = e r 1 − d i s ( o r 1 , d r 1 ) = 13 ddl[1] = e_{r1}-dis(o_{r1},d_{r1})=13 ddl[1]=er1−dis(or1,dr1)=13 , d d l [ 2 ] = e r 1 = 23 ddl[2]=e_{r1}=23 ddl[2]=er1=23。 a r r [ 1 ] = a r r [ 0 ] + d i s ( v 1 , v 2 ) = 6 , a r r [ 2 ] = a r r [ 1 ] + d i s ( v 2 , v 4 ) = 16 arr[1] = arr[0] +dis(v1, v2)=6, arr[2] = arr[1] + dis(v2, v4) = 16 arr[1]=arr[0]+dis(v1,v2)=6,arr[2]=arr[1]+dis(v2,v4)=16. 根据等式8, s l a c k [ ⋅ ] slack[·] slack[⋅]的计算范围为 n = 2 到 0 n=2到0 n=2到0。 s l a c k [ n ] slack[n] slack[n]总是使用 ∞ ∞ ∞初始化,因为所有请求都在 l n l_n ln处传递。 s l a c k [ 1 ] = m i n s l a c k [ 2 ] , d d l [ 2 ] − a r r [ 2 ] = 7 , s l a c k [ 0 ] = m i n s l a c k [ 1 ] , d d l [ 1 ] − a r r [ 1 ] = 7. slack[1] = min{slack[2], ddl[2] − arr[2]} =7, slack[0] = min{slack[1], ddl[1] − arr[1]} = 7. slack[1]=minslack[2],ddl[2]−arr[2]=7,slack[0]=minslack[1],ddl[1]−arr[1]=7. 算法3的3至9行运行如下。 当j=0时,第4行(即 r o u t e ⟨ v 1 , o r 2 , d r 2 , v 2 , v 4 ⟩ route \langle v_1, o_{r2} , d_{r2} , v_2, v_4\rangle route⟨v1,or2,dr2,v2,v4⟩如图2B)违反引理4的(4),因为根据等式5 Δ i , j = d i s ( v 1 , o r 2 ) + d i s ( o r 2 , d r 2 ) + d i s ( d r 2 , v 2 ) − d i s ( v 1 , v 2 ) = 25 > s l a c k [ 1 ] Δ_{i,j}=dis(v_1,o_{r 2})+dis(o_{r2},d_{r2})+dis(d_{r2},v_2)-dis(v_1,v_2)=25>slack[1] Δi,j=dis(v1,or2)+dis(or2,dr2)+dis(dr2,v2)−dis(v1,v2)=25>slack[1](条件为 i = j < n i=j<n i=j<n)。然后我们更新 D i o [ 1 ] = ∞ , P l c [ 1 ] = ∞ Dio[1] = ∞, Plc[1] = ∞ Dio[1]=∞,Plc[1]=∞, 使用等式11和12得到 d e t ( v 1 , o r 2 , v 2 ) = d i s ( v 1 , o r 2 ) + d i s ( o r 2 , v 2 ) − d i s ( v 1 , v 2 ) = 15 > s l a c k [ 0 ] = 7 det(v_1, o_{r2} , v_2) = dis(v_1, o_{r2} ) + dis(o_{r2} , v_2) − dis(v_1, v_2) =15 > slack[0] = 7 det(v1,or2,v2)=dis(v1,or2)+dis(or2,v2)−dis(v1,v2)=15>slack[0]=7。当 j = 1 j=1 j=1时,第4行(即 r o u t e ⟨ v 1 , v 2 , o r 2 , d r 2 , v 4 ⟩ route \langle v_1, v_2, o_{r2} , d_{r2} , v_4\rangle route⟨v1,v2,or2,dr2,v4⟩如图2B)也违反引理4的(4),因为 Δ i , j = d i s ( v 2 , o r 2 ) + d i s ( o r 2 , d r 2 ) + d i s ( d r 2 , v 4 ) − d i s ( v 2 , v 4 ) = 9 > s l a c k [ 1 ] Δ_{i,j} = dis(v_2, o_{r2} ) + dis(o_{r2} , d_{r2} ) +dis(d_{r2} , v_4) − dis(v_2, v_4)=9 > slack[1] Δi,j=dis(v2,or2)+dis(or2,dr2)+dis(dr2,v4)−dis(v2,v4)=9>slack[1]. 在第5行,推论1(2)明显被违反了,因为 D i o [ 1 ] = ∞ Dio[1] = ∞ Dio[1]=∞. 然后我们更新了 D i o [ 2 ] = m i n { D i o [ 1 ] , d e t ( v 2 , o r 2 , v 4 ) } = 5 Dio[2] = min\lbrace Dio[1], det(v2, or2 , v4)\rbrace = 5 Dio[2]=min{Dio[1],det(v2,or2,v4)}=5,因为 p i c k e d [ 1 ] = 1 ≤ K w − K r = 3 picked[1] = 1 ≤ K_w − K_r = 3 picked[1]=1≤Kw−Kr=3并且根据等式11, d e t ( v 2 , o r 2 , v 4 ) = 5 ≤ s l a c k [ 1 ] det(v2, or2 , v4) = 5 ≤ slack[1] det(v2,or2,v4)=5≤slack[1], 根据等式12, 当 D i o [ 1 ] > d e t ( v 2 , o r 2 , v 4 ) 时 P l c [ 2 ] = 2 − 1 = 1 当Dio[1] > det(v_2, o_{r2} , v_4)时Plc[2] = 2 − 1=1 当Dio[1]>det(v2,or2,v4)时Plc[2]=2−1=1.最后,
5. 基于插入的解决方案
5.1 决策阶段
5.1.1 计算 Δ ∗ \Delta^* Δ∗的下界
5.1.2 算法草图
5.2 设计阶段
5.2.1 修剪候选工人
5.2.2 找到最佳工人
5.3 算法草图
6. 实验性研究
这一部分给出了我们提出的算法的实验评估。
6.1 实验设置
数据集.我们对两个真实的全市出租车数据集进行了实验评估。第一篇是由中国成都滴滴出行[3]收集的,它是通过Gaia倡议[4]出版的。第二种是从美国纽约市两种类型的出租车(黄色和绿色)中收集的公共数据集[8],并在以前的大规模共乘研究中用作基准[11][13][39][41]。我们使用当天的数据,要求评估的次数最多(2016年11月18日在成都,2016年4月9日在纽约),分别表示为成都和纽约。两个数据集中的每个元组都是一个由拾取地纬度/经度、放置地纬/经度和释放时间组成的出租车请求。由于只有NYC包含请求容量 K r K_r Kr,我们根据 K r K_r Kr在纽约的分布情况为成都生成 K r K_r Kr。纽约的公路网是从Geofabrik[5]下载的。对于成都,我们使用最新的城市边界[1],并从Geofabrik通过OsmConvert[7]从中国的国家公路网中提取出它的公路网[7]。每个路网都表示为无向图。表4总结了每个图中的请求数以及顶点和边的数量。“纽约公约”是现有研究[25][17][41][18][30][11][13]中最大的数据集。例如,“纽约公约”中的件事,比[25][17]中使用的公路网大6.6倍和11.1倍。“纽约公约”的请求数量比[41]多47.7%。成都拥有比现有文献更大的路网和可比的需求。
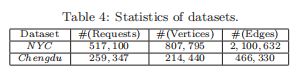
成果.我们模拟了在[25][13]中的设置下具有代表性的共享移动应用程序。每个请求的起源和目的地都预先映射到道路网络中最近的顶点。从路网中的顶点中随机选取工人的初始位置。当员工请求服务时,他/她按照计划的路线移动到目的地。由于的士通常在不同类型的道路上以不同的速度行驶,例如23米/秒的高速公路或6米/秒的住宅街道,我们为每一种道路指定一个恒定的速度,即其城市最高法定车速的80%[2],并假定出租车在不同类型的道路上以不同的速度行驶。表5总结了实验的主要参数。默认值以粗体标记。交付截止日期计算为表中的参数添加的请求的释放时间。例如,具有发布时间 t r t_r tr的请求的默认截止日期是 t r + 10 t_r+10 tr+10分钟。 K w K_w Kw是使用μ=3,···,20的高斯分布产生的,因为两个数据集都没有指定这些信息。我们将α修正为1,使得方程中 U C ( W , R ) UC(W,R) UC(W,R)的第一个项相等于总行程。请求的惩罚由表中的参数乘以请求的起源和目的地之间的最短距离来设置,例如,缺省情况下 p r = 10 × d i s ( o r , d r ) pr=10×dis(o_r,d_r) pr=10×dis(or,dr)。注意, α α α固定为1, p r = 2 , ⋅ ⋅ , 50 ( × d i s ( o r , d r ) ) p_r=2,··,50(×dis(o_r,d_r)) pr=2,⋅⋅,50(×dis(or,dr)),这相当于在总收入最大化时调整 c r c_r cr和 c w c_w cw之间的比例。纽约的 p r p_r pr和 ∣ W ∣ \mid W\mid ∣W∣都比成都要大,因为他们拥有更大的道路网络和司机数量。
实验在40 Intel®Xeon®E5 2.30GHz处理器的服务器上进行,该处理器支持超线程,内存128 GB。该仿真实现是单线程的,成都和NYC的总运行时间(不包括最短路径和距离查询的空间索引和标签)限制在10/20小时。根据[25]关于实时乘车共享的一些工作的结果,实时解决方案应该在时间限制之前停止。所有算法都是用GNU C++语言实现的。每个实验设置重复30次,并报告了平均结果。我们只通过加权邻接表存储路网的顶点和边(即图)。最短距离查询和最短路径查询都是在运行中进行的,使用了一种基于集线器的道路网络标记算法[9]。LRU缓存[25]用于最短距离和路径查询,并由所有算法使用。
比较算法.我们将pruneGreedyDP与以下最先进的算法进行了比较。
- tsahre[30].它首先通过搜索过程过滤工作人员,然后应用基本插入来查找每个新请求的增加距离最小的工作人员。
- kinetic[25].它使用一个动态树来维护所有可能的路由,以服务所有剩余的请求。与tshare不同,插入操作是基于树结构递归执行的。
- batch[11].它首先在一个批处理中生成一组请求(例如,6秒)并对组进行排序。然后,通过将每个请求插入到当前工作人员的路由中,贪婪地分配每个组中的请求,最后选择能够以最小的增加距离服务更多请求的工作人员。
- GreedyDP.它是我们在引理8中没有剪枝策略的pruneGreedyDP算法的一个变体。
指标.指标。所有算法都根据统一总成本、服务率 ( ∣ R + ∣ / ∣ R ∣ ) (\mid R^+ \mid/\mid R\mid) (∣R+∣/∣R∣)和响应时间(处理单个请求的平均等待时间)(Resp)进行评估。服务速率和响应时间是许多大型实时搭便车方案[30][25]中的衡量标准。我们还评估了每种算法的内存开销。请注意,与图形、缓存和网格索引的大小相比,可以省略辅助数组的内存使用情况。由于图和缓存的内存开销对于每种算法都是恒定的,因此我们只在改变网格g的大小时计算网格索引的内存开销。我们还评估了剪枝与GreedyDP之间保存的最短距离查询(简称距离查询)的数量,以显示剪枝策略的有效性。
6.2 实验结论
对工人人数的影响 ∣ W ∣ \mid W\mid ∣W∣.
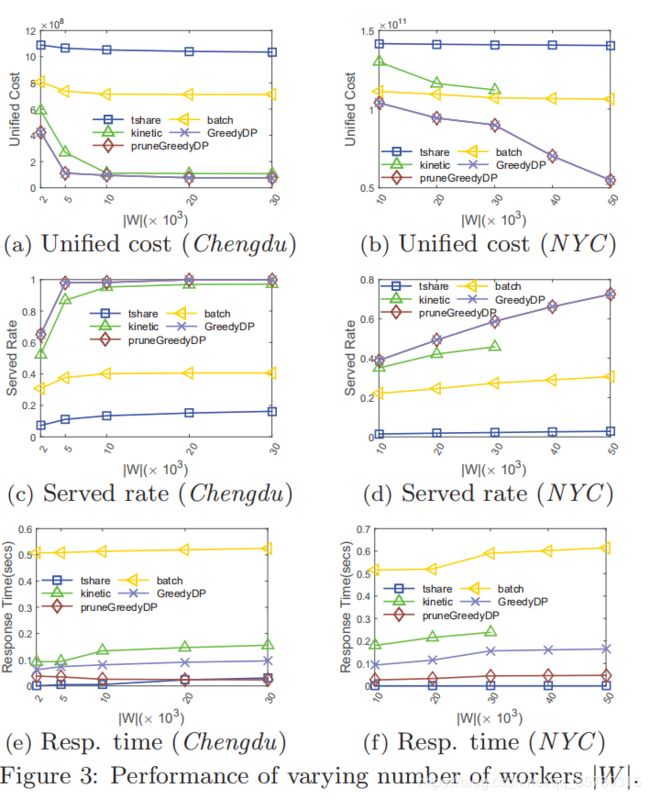
图3示出了改变工人数量的结果。整体而言,在统一成本方面,在成都和纽约,pruneGreedyDP的表现比其他公司高出12.41%至85.36%。所有算法的统一成本随着工作人员的增加而降低,因为可以满足更多的请求。出于同样的原因,所有算法在这两个数据集中的服务率都会增加。pruneGreedyDP有最高的服务率——54.94%,比batch高141.61%。成都市的服务率结果表明,当服务请求数量最大化时,pruneGreedyDP可与kinetic竞争并且明显比batch好。对于较大规模的道路网络,所有算法的服务率都显著降低,这与引理1一致,即服务请求的数量受到了 ∣ V ∣ \mid V\mid ∣V∣的影响。所有基线的响应时间都随 ∣ W ∣ \mid W\mid ∣W∣的增加而增加。tshare是最快的,因为它的搜索过程错误地删除了许多可能的工作人员,从而导致了最低的服务率(从1%到16%)。pruneGreedyDP是第二快的,比kinetic和batch快2.46到32.08倍。请注意,在20h内,kinetic不能完成模拟,而在 ∣ W ∣ \mid W\mid ∣W∣=40k和50k的情况下。采用所提出的剪枝策略,纽约市的最短距离查询总数从52.7亿条增加到422.2亿条,成都市从22.6亿条增加到451.6亿条。因此,pruneGreedyDP的响应时间比GreedyDP平均快2.76倍,验证了我们的剪枝策略的效率。
对工人容量的影响 K w K_w Kw.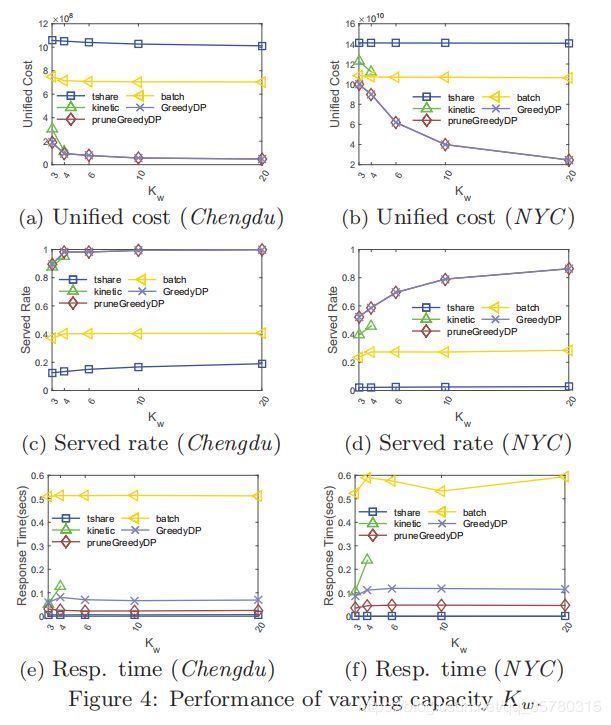
图4显示了改变工人能力的结果。随着容量的增大,所有算法在成都的统一成本都较低。我们的pruneGreedyDP算法的统一成本比其他算法低71%。kinetic不能在大 K w K_w Kw的情况下停止,因为它的指数时间复杂度为 ( 2 K w ) ! (2K_w)! (2Kw)![17]。相比之下,batch更稳定,统一成本略有下降。就服务率而言,pruneGreedyDP仍是最好的,比其他的高出96%。就响应时间而言,tshare是最快的,其原因与改变员工数量的原因相同。在成都市,pruneGreedyDP的反应时间比kinetic和batch缩短41%-95%,在纽约减少47%-93%。
网格大小 g g g的影响.
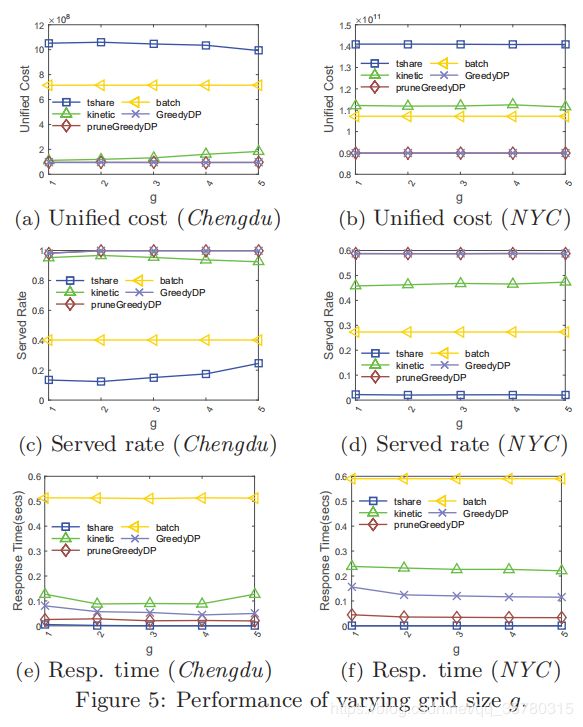
图5绘制了改变网格大小g的结果。在统一成本方面,kinetic和tshare对网格大小的变化都相对不敏感,pruneGreedyDP在这两个数据集中输出的统一成本最低。就服务率而言,成都市的batch产量几乎一直保持在40.1%,纽约的产量为25.7%。在两个数据集上,pruneGreedyDP的服务率最高,分别比成都市的基线高出3.0%和87.6%,在纽约则分别高出16.9%和96.5%。同样,tshare的响应时间最短,但服务速率极低。在响应时间上,kinetic和batch处理速度分别是pruneGreedyDP的3.11倍和25.98倍。对于网格索引的内存使用,tshare在NYC的消耗最大,在609.46到5.38MB之间,在成都,在9389.72到326.98 MB之间,而其他的在成都和NYC的消耗分别高达0.30MB和3.23MB。这是因为其他算法的网格索引只在网格中存储工作人员的ID,而不是像tshare这样的排序网格列表。
截至时间 e r e_r er的影响.
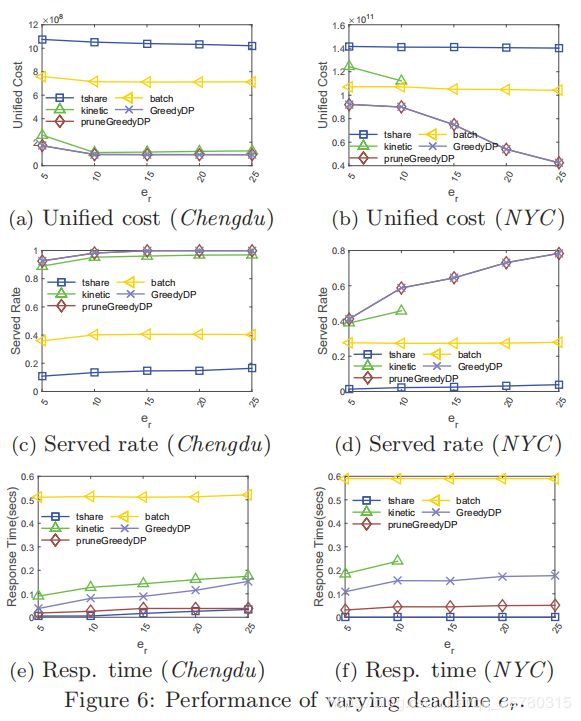
图6示出了改变截止日期er的结果。随着最后期限的增大,所有算法的统一代价降低,而算法的服务率增加。其原因是,较长的最后期限可以提供更多的请求,从而降低统一费用和较高的服务费率。就效益(统一成本和服务率)而言,pruneGreedyDP仍然是最好的。请注意,当α=1且服务率接近100%时,统一成本接近总行程。因此,pruneGreedyDP产生的旅行距离比kinetic[25]和tshare[30]小。batch和pruneGreedyDP的响应时间稳定,而其它处理的响应时间显著增加。当 e r e_r er从5 min增加到25 min时,GreedyDP的增幅分别为1.63倍和4.12倍。相反,pruneGreedyDP的响应时间保持在50 ms以内。这是因为,使用新的修剪策略,在成都节省了24.95至83.99亿次最短距离查询,在纽约省了16.43至579亿次查询。
惩罚 p r p_r pr的影响.
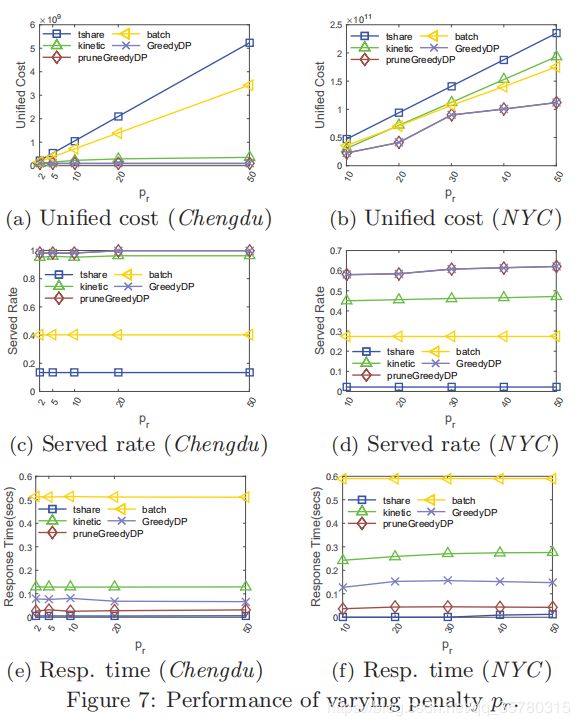
图7示出了改变惩罚的结果。所有基线的统一成本随代价的增加而增加,而修剪的代价总是最小的。这表明,当 c r c_r cr和 c w c_w cw之间的比例变化时,当总收入最大化时,pruneGreedyDP实际上仍然具有竞争力。kinetic的服务率略有增加,因为较高的惩罚可能会迫使它尝试提供更多的请求,即在决策阶段 p r p_r pr大于 α ⋅ m i n L B α·minLB α⋅minLB时。在响应时间方面,我们提出的算法比kinetic和batch快4.17倍和16.34倍。
结果总结.我们总结我们的实验结果如下。
- 我们的pruneGreedyDP算法通常比三种最先进的算法[25][11]的统一成本低1.2到12.8倍,同时能够在大规模数据集中服务更多的请求(至少高出9%)。这些结果验证了我们的解决方案在多目标路径规划中的有效性。
- 基于DP的插入算法GreedyDP和pruneGreedyDP比最先进的[25][11]快2.62至20.72倍。在许多情况下,由于节省了数百亿个最短距离查询,pruneGreedyDP比GreedyDP快2.8倍。
- 在最先进的技术中,kinetic[25]由于其指数时间复杂性,常常无法在大规模数据集上停留时间。batch[11]的有效性和效率不如我们的解决方案,但在大规模数据集中比kinetic更可扩展。tshare[30]总是响应时间最快,但服务速率最低,统一成本最高。
7. 总结
在本文中,我们提出了URPSM问题,即共享移动性路由规划的统一公式。它提供了一个灵活的多目标函数,可以将现有研究中的主流优化目标归结为URPSM问题的特殊情况。我们证明了不存在具有恒竞争比的多项式时间算法来解决以往研究中提出的URPSM问题及其变量。由于插入是许多现有路由规划方案中的一种基本而效率低下的操作,本文提出了一种新的基于动态规划的算法,该算法将插入的时间复杂度从三次或二次时间降为线性时间。然后,我们设计了一个有效和高效的两阶段解决方案,利用上述基于DP的插入算法来近似地解决URPSM问题。在实际数据集上的大量实验表明,我们提出的解决方案在有效性和效率方面都远远超过了目前的技术水平。本文为共享移动环境下的路由规划提供了全面的理论参考,为今后的研究提供了新的机遇,为大规模共享移动应用设计有效的解决方案提供了新的思路。
8.参考资料
[1] Boundary of Chengdu.https://www.openstreetmap.org/node/244077729.
[2] Default Speed Limits in OpenStreetMap. https://wiki.openstreetmap.org/wiki/OSM_tags_for_routing/Maxspeed.
[3] Didi Chuxing. http://www.didichuxing.com/.
[4] GAIA.https://outreach.didichuxing.com/research/opendata/.
[5] Geofabrik. https://download.geofabrik.de/.
[6] OpenStreetMap.http://www.openstreetmap.com/.
[7] Osmconvert.
https://wiki.openstreetmap.org/wiki/Osmconvert.
[8] TLC Trip Record Data. http://www.nyc.gov/html/tlc/html/about/trip_record_data.shtml.
[9] I. Abraham, D. Delling, A. V. Goldberg, and R. F.Werneck. A hub-based labeling algorithm for shortest paths in road networks. In International Symposium on Experimental Algorithms, pages 230–241, 2011.
[10] N. Agatz, A. Erera, M. Savelsbergh, and X. Wang. Optimization for dynamic ride-sharing: A review. European Journal of Operational Research,223(2):295–303, 2012.
[11] J. Alonso-Mora, S. Samaranayake, A. Wallar,E. Frazzoli, and D. Rus. On-demand high-capacity
ride-sharing via dynamic trip-vehicle assignment.Proceedings of the National Academy of Sciences,
114(3):462–467, 2017.
[12] N. Ascheuer, S. O. Krumke, and J. Rambau. Online dial-a-ride problems: Minimizing the completion time. In Annual Symposium on Theoretical Aspects of Computer Science, pages 639–650, 2000.
[13] M. Asghari, D. Deng, C. Shahabi, U. Demiryurek, and Y. Li. Price-aware real-time ride-sharing at scale: an auction-based approach. In SIGSPATIAL, pages 3:1–3:10, 2016.
[14] M. Asghari and C. Shahabi. An on-line truthful and individually rational pricing mechanism for
ride-sharing. In SIGSPATIAL, pages 7:1–7:10, 2017.
[15] A. Borodin and R. El-Yaniv. Online computation and competitive analysis. Cambridge University Press, 2005.
[16] M. Charikar and B. Raghavachari. The finite capacity dial-a-ride problem. In FOCS, pages 458–467, 1998.
[17] L. Chen, Q. Zhong, X. Xiao, Y. Gao, P. Jin, and C. S. Jensen. Price-and-time-aware dynamic ridesharing. In ICDE, pages 1061–1072, 2018.
[18] P. Cheng, H. Xin, and L. Chen. Utility-aware ridesharing on road networks. In SIGMOD, pages
1197–1210, 2017.
[19] B. Cici, A. Markopoulou, and N. Laoutaris. Designing an on-line ride-sharing system. In SIGSPATIAL, pages 60:1–60:4, 2015.
[20] G. B. Dantzig and J. H. Ramser. The truck dispatching problem. Management science, 6(1):80–91,1959.
[21] P. M. d’Orey, R. Fernandes, and M. Ferreira. Empirical evaluation of a dynamic and distributed taxi-sharing system. In 15th International IEEE Conference on Intelligent Transportation Systems,
pages 140–146, 2012.
[22] E. Feuerstein and L. Stougie. On-line single-server dial-a-ride problems. Theoretical Computer Science, 268(1):91–105, 2001.
[23] A. Gupta, M. Hajiaghayi, V. Nagarajan, and R. Ravi. Dial a ride from k-forest. ACM Transactions on Algorithms (TALG), 6(2):41, 2010.
[24] W. M. Herbawi and M. Weber. A genetic and insertion heuristic algorithm for solving the dynamic ridematching problem with time windows. In Proceedings of the 14th annual conference on Genetic and evolutionary computation, pages 385–392, 2012.
[25] Y. Huang, F. Bastani, R. Jin, and X. S. Wang. Large scale real-time ridesharing with service guarantee on road networks. PVLDB, 7(14):2017–2028, 2014.
[26] H. Hung, R. Chapman, W. Hall, and E. Neigut. A heuristic algorithm for routing and scheduling
dial-a-ride vehicles. In ORSA/TIMS National Meeting, 1982.
[27] J. J. Jaw. Solving large-scale dial-a-ride vehicle routing and scheduling problems. PhD thesis,
Massachusetts Institute of Technology, 1984.
[28] J. J. Jaw, A. R. Odoni, H. N. Psaraftis, and N. H. M. Wilson. A heuristic algorithm for the multi-vehicle advance request dial-a-ride problem with time windows. Transportation Research Part B
Methodological, 20(3):243–257, 1986.
[29] A. Kleiner, B. Nebel, and V. A. Ziparo. A mechanism for dynamic ride sharing based on parallel auctions. In IJCAI, volume 11, pages 266–272, 2011.
[30] S. Ma, Y. Zheng, and O. Wolfson. T-share: A large-scale dynamic taxi ridesharing service. In ICDE, pages 410–421, 2013.
[31] S. Ma, Y. Zheng, and O. Wolfson. Real-time city-scale taxi ridesharing. IEEE Transactions on Knowledge and Data Engineering, 27(7):1782–1795, 2015.
[32] R. Mole and S. Jameson. A sequential route-building algorithm employing a generalised savings criterion. Journal of the Operational Research Society, 27(2):503–511, 1976.
[33] M. Ota, H. Vo, C. Silva, and J. Freire. A scalable approach for data-driven taxi ride-sharing simulation. In Big Data, pages 888–897, 2015.
[34] M. Ota, H. Vo, C. Silva, and J. Freire. Stars: Simulating taxi ride sharing at scale. IEEE Transactions on Big Data, PP(99):1–1, 2017.
[35] D. Pelzer, J. Xiao, D. Zehe, M. H. Lees, A. C. Knoll, and H. Aydt. A partition-based match making algorithm for dynamic ridesharing. IEEE Transactions on Intelligent Transportation Systems,
16(5):2587–2598, 2015.
[36] S. Roy and U. de Montr´eal. Centre de recherche sur les transports. The construction of routes and schedules for the transportation of the handicapped. Montr´eal: Universit´e de Montr´eal, Centre de recherche sur les transports, 1983.
[37] Z. B. Rubinstein, S. F. Smith, and L. Barbulescu. Incremental management of oversubscribed vehicle schedules in dynamic dial-a-ride problems. In AAAI, pages 1809–1815, 2012.
[38] S. Shaheen, A. Cohen, and I. Zohdy. Shared mobility: Current practices and guiding principles. Technical report, 2016.
[39] P. Santi, G. Resta, M. Szell, S. Sobolevsky, S. H. Strogatz, and C. Ratti. Quantifying the benefits of vehicle pooling with shareability networks. Proceedings of the National Academy of Sciences, 111(37):13290–13294, 2014.
[40] D. O. Santos and E. C. Xavier. Dynamic taxi and ridesharing: A framework and heuristics for the optimization problem. In IJCAI, volume 13, pages 2885–2891, 2013.
[41] R. S. Thangaraj, K. Mukherjee, G. Raravi, A. Metrewar, N. Annamaneni, and K. Chattopadhyay.
Xhare-a-ride: A search optimized dynamic ride sharing system with approximation guarantee. In
ICDE, pages 1117–1128, 2017.
[42] Y. Tong, Y. Zeng, Z. Zhou, L. Chen, J. Ye, and K. Xu. A unified approach to route planning for
shared mobility. http://home.cse.ust.hk/~yzengal/yz.pdf, 2018.
[43] N. H. Wilson, R. Weissberg, B. Higonnet, and J. Hauser. Advanced dial-a-ride algorithms. Technical report, 1975.
[44] N. H. Wilson, R. W. Weissberg, and J. Hauser. Advanced dial-a-ride algorithms research project. Technical report, 1976.
[45] SUMC. What is shared-use mobility? https://goo.gl/3Jw6z7, 2018.
[46] A. C. C. Yao. Probabilistic computations: Toward a unified measure of complexity. In FOCS, pages 222–227, 1977.
[47] S. Yeung, E. Miller, and S. Madria. A flexible real-time ridesharing system considering current road conditions. In MDM, volume 1, pages 186–191, 2016.
[48] Y. Zheng. Trajectory data mining: an overview. ACM Transactions on Intelligent Systems and Technology (TIST), 6(3):29, 2015.