计算几何作业(下)
HDU 3320 openGL
重要的就是绕任意轴旋转这个离谱操作。
我们把绕一个轴顺时针旋转视为正方向(从轴的负方向往正方向看。)
其中坐标系如图所示:
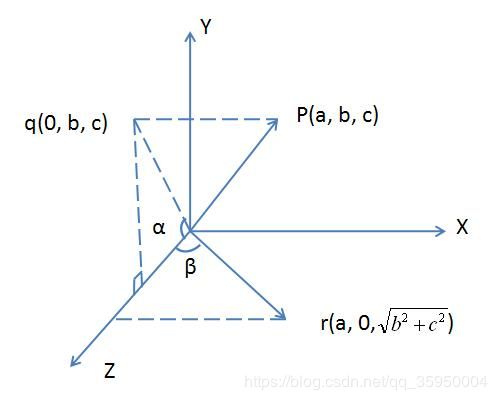
那么容易发现绕 z z z轴旋转正的 α \alpha α的角度。
相当于在 O x y Oxy Oxy平面上顺时针绕 α \alpha α,
也就是 x ′ = r cos ( θ + α ) = x cos α − y sin α , y ′ = r s i n ( θ + α ) = y cos α + x sin α = sin α x + cos α y x' = r\cos(\theta + \alpha) =x\cos\alpha-y\sin\alpha, y' = rsin(\theta + \alpha) = y\cos\alpha+x\sin \alpha = \sin \alpha x + \cos \alpha y x′=rcos(θ+α)=xcosα−ysinα,y′=rsin(θ+α)=ycosα+xsinα=sinαx+cosαy
写成行向量乘矩阵的形式就是 [ x ′ y ′ z 1 ] = [ x y z 1 ] × ( R z ( α ) = [ cos α sin α 0 0 − sin α cos α 0 0 0 0 1 0 0 0 0 1 ] ) \begin{bmatrix}x'&y'&z&1\end{bmatrix} = \begin{bmatrix}x&y&z&1\end{bmatrix} \times\left(R_z(\alpha) = \begin{bmatrix}\cos \alpha&\sin\alpha&0&0 \\-\sin\alpha&\cos\alpha &0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}\right) [x′y′z1]=[xyz1]×⎝⎜⎜⎛Rz(α)=⎣⎢⎢⎡cosα−sinα00sinαcosα0000100001⎦⎥⎥⎤⎠⎟⎟⎞
因为 x , y , z x,y,z x,y,z是轮换的(你想象上面的图是一个玩具,把 z z z翻到上面, y y y就会到右边, x x x就会到之前 z z z的位置。)
所以我们可以简单的通过轮换式的性质得到绕 y y y轴旋转 α \alpha α度的变换矩阵。
R y ( α ) = [ cos α 0 − sin α 0 0 1 0 0 sin α 0 cos α 0 0 0 0 1 ] R_y(\alpha)=\begin{bmatrix}\cos \alpha&0&-\sin\alpha&0 \\\ 0&1 &0&0\\\sin\alpha&0&\cos \alpha&0\\0&0&0&1\end{bmatrix} Ry(α)=⎣⎢⎢⎡cosα 0sinα00100−sinα0cosα00001⎦⎥⎥⎤
(如何轮换?发现这就是在左上角 3 × 3 3\times 3 3×3的矩阵里面每个点都往左上循环位移了一位。)
所以以 x x x轴为中心旋转 α \alpha α度的矩阵?(读者可以自己想想)
为:
R x ( α ) = [ 1 0 0 0 0 cos α sin α 0 0 − sin α cos α 0 0 0 0 1 ] R_x(\alpha)=\begin{bmatrix}1&0&0&0 \\\ 0&\cos\alpha &\sin\alpha &0\\\ 0&-\sin\alpha&\cos \alpha&0\\0&0&0&1\end{bmatrix} Rx(α)=⎣⎢⎢⎡1 0 000cosα−sinα00sinαcosα00001⎦⎥⎥⎤
回到正题,如何让一个点 x , y , z x,y,z x,y,z对轴 ( 0 , 0 , 0 ) → ( a , b , c ) (0,0,0) \rightarrow (a,b,c) (0,0,0)→(a,b,c)逆时针旋转 θ \theta θ度?
可以发现逆时针就是我们的正方向。
先说结论:
设 cos α = c b 2 + c 2 , sin β = a a 2 + b 2 + c 2 \cos\alpha = \frac c{\sqrt {b^2+c^2}} , \sin\beta = \frac {a}{\sqrt {a^2+b^2+c^2}} cosα=b2+c2c,sinβ=a2+b2+c2a
转移矩阵是 R x ( α ) R y ( − β ) R z ( θ ) R y ( β ) R x ( − α ) R_x(\alpha)R_y(-\beta)R_z(\theta)R_y(\beta)R_x(-\alpha) Rx(α)Ry(−β)Rz(θ)Ry(β)Rx(−α)
其实就是前两个矩阵换基后直接按 z z z轴转再用后两个矩阵把基换回来。
注意实际上 β \beta β的算法直接用 arcsin \arcsin arcsin就是正确的,因为上式已经考虑了 a a a的正负,又因为是第二步,所以 b , c b,c b,c的正负被压起来了不用考虑。
但是 α \alpha α需要考虑 b b b和 c c c的正负,所以建议直接使用 a t a n 2 atan2 atan2。
另,此题写 l o n g d o u b l e \rm long\ double long double会 W A \rm WA WA,建议全程用 d o u b l e \rm double double,并大骂垃圾杭电
浓浓的线性代数味
A C C o d e \mathcal AC \ Code AC Code
#includeHDU 4116 Fruit Ninja
求一条线与最多的圆相交。
枚举一个圆,假设答案的线一定是这个圆的切线。
然后对于其他圆求出公切线,按照极角序排序后加一减一之类的即可维护出切点关于枚举的圆在某一极角处会和多少圆相交。
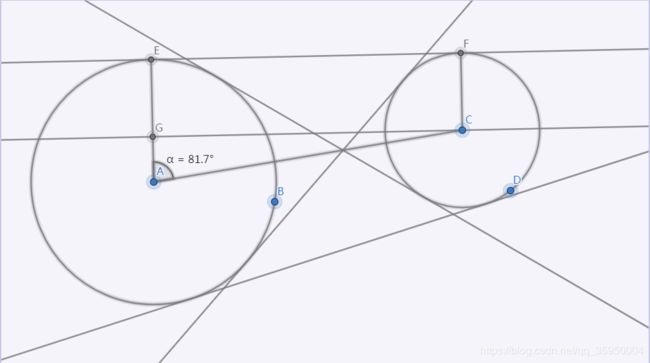
如何求圆的公切线:
假设 r 1 ≥ r 2 r_1 \geq r_2 r1≥r2。
- 圆心距 d < r 1 − r 2 d \lt r_1 - r_2 d<r1−r2
内含,无解。 - d = r 1 − r 2 d = r_1 - r_2 d=r1−r2
有两条重合的外公切线,对于此题可以在切点极角 ± e p s \pm eps ±eps处 ± 1 \pm 1 ±1 - d > r 1 − r 2 d \gt r_1-r_2 d>r1−r2
求出图中外公切线的切点 ,可以通过 arccos ( r 1 − r 2 d ) = α \arccos(\frac {r_1-r_2}{d}) = \alpha arccos(dr1−r2)=α来得到。
3.1 d < r 1 + r 2 d \lt r_1+r_2 d<r1+r2 无内公切线。
3.2 d = r 1 + r 2 d = r_1 + r_2 d=r1+r2 有两条重合内公切线但实际在本题无意义。
3.3 d > r 1 + r 2 d \gt r_1 + r_2 d>r1+r2 有两条内公切线,可以通过 arccos ( r 1 + r 2 d ) = β \arccos(\frac {r_1+r_2}{d}) = \beta arccos(dr1+r2)=β来得到。
另一个圆对应的切点也很简单但是此题不需要。
C o d e Code Code(HDU交不了)
#includeHDU 5784 How Many Triangles
n ≤ 2000 n \leq 2000 n≤2000个点求锐角三角形个数。
我怎么觉得三方能过。
我怎么看着这像KD树
枚举钝角的点然后极角排序即可。
n n n点共线恶心坏了。
A C C o d e \mathcal AC \ Code AC Code
#includeHDU 5017 Ellipsoid
求一个点到椭球面的最小距离。
假设空间是 n n n维的,为 x = ( x 1 , x 2 , x 3 . . . x n ) x = (x_1,x_2,x_3...x_n) x=(x1,x2,x3...xn)
那么如果我们有一个表达式 f ( x ) = ∑ i = 1 n ∑ j = i n a i , j x i x j f(x) = \sum_{i=1}^n \sum_{j=i}^n a_{i,j} x_ix_j f(x)=∑i=1n∑j=inai,jxixj(题目中给出的椭圆面的形式就可以用这个形式表达)
我们当 i ≠ j i\neq j i=j时把 a i , j a_{i,j} ai,j分成两半: b i , j = a i , j 2 b_{i,j} = \frac {a_{i,j}}2 bi,j=2ai,j,其他时候 b i , i = a i , i b_{i,i} = a_{i,i} bi,i=ai,i
可以发现 b i , j b_{i,j} bi,j形成的矩阵 B B B,满足 f ( x ) = x B x T f(x) = xBx^T f(x)=xBxT
所以现在就可以开始线性代数了。
发现这个 B B B是一个实对称矩阵,他一定和一个对角矩阵相似。
这是因为如果我们求出 B B B的所有 n n n个特征值 λ i \lambda_i λi和特征向量 p i p_i pi(这里是列向量),特征向量互不相同
因为 A p = λ p Ap = \lambda p Ap=λp所以有 A [ p 1 , p 2 , p 3 . . . p n ] = [ p 1 , p 2 , p 3 . . . p n ] d i a g ( λ 1 , λ 2 . . . λ n ) A\begin{matrix}[p_1,p_2,p_3...p_n]\end{matrix} = \begin{matrix}[p_1,p_2,p_3...p_n]\end{matrix}diag(\lambda_1,\lambda_2...\lambda_n) A[p1,p2,p3...pn]=[p1,p2,p3...pn]diag(λ1,λ2...λn)
这里 d i a g ( a i ) diag(a_i) diag(ai)指的是一个对角矩阵,只有主对角线有值,其中 m i , i = a i m_{i,i} = a_i mi,i=ai。
然后我们把 [ p 1 , p 2 , p 3 . . . p n ] [p_1,p_2,p_3...p_n] [p1,p2,p3...pn]除过去就可以得到一个矩阵 P = [ p 1 , p 2 , p 3 . . . p n ] P = [p_1,p_2,p_3...p_n] P=[p1,p2,p3...pn]满足
P − 1 A P P^{-1}AP P−1AP等于一个对角矩阵。
但是这和 x B x T xBx^T xBxT有什么关系呢?
考虑如果 P P P是一个正交矩阵,那么有 P P T = I PP^T = I PPT=I,所以 P T = P − 1 P^T = P^{-1} PT=P−1,(因为特征向量可以任意同时变大或缩小,所以只要 P P T = k I PP^T = kI PPT=kI我们就可以放缩得到这个 P P P,而 P P T = k I PP^T = kI PPT=kI需要的是这个矩阵有 n n n个互不相同的特征向量。)
那么我们把 P T B P = P^TBP= PTBP=一个对角矩阵 R R R。
B = ( P − 1 ) T R P − 1 = P R P T B =(P^{-1})^T RP^{-1} = PRP^T B=(P−1)TRP−1=PRPT
x B x T = x P R P T x T = ( x P ) R ( x P ) T xBx^T = xPRP^Tx^T= (xP)R(xP)^T xBxT=xPRPTxT=(xP)R(xP)T
也就是说我们把 n n n维基底做一个线性变换 P P P,换个元,
就可以得到标准式 f ( x ) = g ( y ) = ∑ i = 1 n R i , i y i 2 f(x) = g(y) = \sum_{i=1}^n R_{i,i}y_i^2 f(x)=g(y)=∑i=1nRi,iyi2
在这题里面有 g ( y ) = 1 g(y) = 1 g(y)=1
我们假设 p p p是 R i , i R_{i,i} Ri,i中的最大值。
所以 g ( y ) = 1 ≤ p ∑ i = 1 n y i 2 g(y) = 1 \leq p\sum_{i=1}^n y_i^2 g(y)=1≤p∑i=1nyi2
也就是说在换了基底之后我们可以愉悦的得到和原点的距离 ∑ i = 1 n y i 2 ≥ 1 p \sqrt {\sum_{i=1}^n y_i^2} \geq \frac 1{\sqrt p} ∑i=1nyi2≥p1
就像是你把一个对称轴不是 x , y x,y x,y轴的椭圆旋转(线性变换)得到了一个对称轴在 x , y x,y x,y轴上的椭圆,那么你离原点的最短距离显然就是取短轴的端点也就是一维取满别的取 0 0 0。
所以这个最小值是可以验证得到的。
那么只需要求出 R R R也就是矩阵的特征值即可。
对于这个题就是解一元三次方程,得复习盛金公式了。(然后发现下面的代码写的是牛顿迭代。。。)
需要注意的是上面的叙述忽略了为什么实对称矩阵一定有 n n n个互不相同的特征向量(特征值相同在上面的证明中不影响。)
具体可以看百度的这个回答:
看了上面的帖子 甚至还有n个线形无关的特征值的论述. 我不得不说说我的观点。来源于课本。应该说每个矩阵都有n个特征值 因为特征方程都是n阶多项式。不能因为有的特征值有重数,而否认它的存在。不可能因为双胞胎一样,而忽略掉。 问题在于矩阵的几何重数等于代数重数。也就是每个特征值的重数与其基础解系的解向量的个数相等。实对称矩阵能够对角化的原因是其特征值的几何重数等于其代数重数,也就是每个特征值的重数与其对应的基础解系的解向量的个数相等。至于为什么相等,这个教材上也省略了。说是太高深。补充,特征值的几何重数小于代数重数。这个证明也好像比较高深。教材也省略。所以,如果每个特征值为1重的话,则其几何重数为一,也就是与其次特征值对应的基础解系的解向量的个数为一。所以,n个互不相等的特征值,则对应n个互不相关的特征向量。这是个可对角化的必要非充分条件。但有的矩阵有相同的特征值,比如说某个特征值代数重数为2,那么它所对应的几何重数或者为一,或者为二,(特征值的几何重数小于代数重数),也就是说2个特征值都只对应一个特征向量。那么n个特征值必然不能有n个特征相量线性无关。从而不能保证对角化。 而实对称矩阵恰好没有这种尴尬的局面产生。至于证明,建议考数学研究生或者自学。
建议考数学研究生或者自学
代码咕咕咕了。
一句话题解:
用特征根方法把 a x 2 + b y 2 + c z 2 + d x y + e y z + f x z = 1 ax^2+by^2 +cz^2 +dxy+eyz+fxz=1 ax2+by2+cz2+dxy+eyz+fxz=1
看做一个线性变换,求这个线性变换矩阵的的特征方程的根 ϕ , β , γ \phi ,\beta,\gamma ϕ,β,γ
把原方程换基(在这个题中是旋转)转换为 ϕ X 2 + β Y 2 + γ Z 2 = 1 \phi X^2 + \beta Y^2 + \gamma Z^2 = 1 ϕX2+βY2+γZ2=1
然后类比高中椭圆求到原点的最小距离得到,
这个椭球面到原点的最小距离就是 1 max ( ϕ , β , γ ) \sqrt {\frac 1{\max(\phi,\beta,\gamma)}} max(ϕ,β,γ)1。
A C C o d e \mathcal AC\ Code AC Code
#includeHDU 3644 A Chocolate Manufacturer’s Problem
问 n n n边形内能否放入一个大小为 R R R的圆。