7、与神经网络学习相关的参数(SGD、adam等)
1 参数的更新
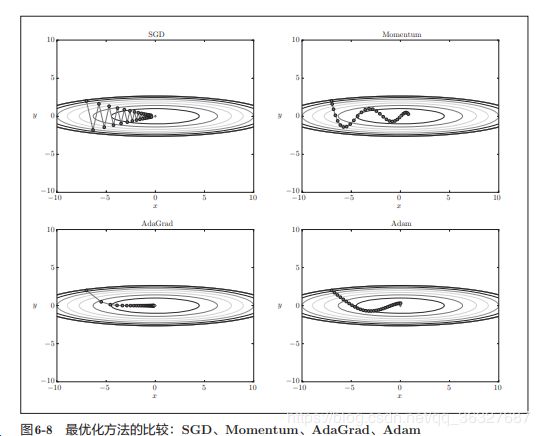
四种方法:见图
01 随机梯度下降法:SGD
使用参数的梯度,沿着梯度方向更新参数,并且重复这个步骤多次,从而逐渐靠近最优参数,这个过程称为随机梯度下降法
# 源代码
class SGD:
def _init_(self,lr=0.01):
self.lr=lr
def update(self,params,grads): # params,和grads是字典型变量
# 代码段的update(params,grads),会被反复调用按照params['W1']、grads['W1'],
#分别保存了权重参数和他们的梯度。
for k inparams.keys():
params(key)-=self.lr*grads[key]
见图:SGD呈之字形移动, 这是一个相当低效的路径。
SGD的缺陷就是,如果函数的形状非均向,比如延伸状,搜索的路径就会非常抵消。
低效率的最根本原因是,梯度的方向没有指向最小的方向。
02 Momentum 方法
Mnmentum是“动量”的意思,和物理有关。
源代码程序实现
class Momentum:
def _init_(self,lr=0.01,momentum=0.9):
self.lr=lr
self.momentum=momentum
self.v=None
def update(self,params,grads):
if self.v is None:
self.v={}
for key,val in params.items():
self.v[key]=np.zeros_like(val)
for key in params.keys():
self.v[key]=self.momentum*self.v[key]-self.lr*grads[keys]
params[key]+=self.v[key]
实例变量v会保存物体的速度,初始化时候,v中什么都不保存,但是当第一次调用update()的时候
v会以字典型变量的形式保存与参数结构相同的数据
和SGD相比,可以更快地朝x轴方向靠近,减弱“之”字形的变动程度。
03 AdaGrad方法
在神经网络的学习中,学习率(数学式中记为y)的值很重要,学习率过小,会导致学习花费过多时间,反过来
学习率过大,则回到自学习发散而不能正确进行
学习率衰减(learning rate decay)
随着学习的进行,使学习率逐渐减小。
AdaGrad:会为每个元素适当地调整学习率,与此同时进行学习
源代码:
class AdaGrad:
def _init_(self,lr=0.01):
self.lr=lr
self.h=None
def update(self,params,grads):
if self.h is None:
self.h={}
for key,val in params.items():
self.h[key]=np.zeros_like(val)
for key in params.keys():
self.h[key]+=grads[key]*grads[key]
paras[key]-=self.lr*grads[key]/(np.sqrt(self.h[key])+le-7)
注意:最后一行加上了微小值le-7.这是为了防止当self.h[key]中有0的时候,
将0用做除数的情况。在很多深度学习的框架中,这个微小值也可以设定为参数。这里选择固定值
04 Adam
Momentum 参照小球在碗中滚动的物理规则进行移动,AdaGrad为参数的每个元素适当地调整更新不发。
Adam结合了前面两种方法的优点,有望实现参数空间的高效搜索。
Adam会设置3个参数,一个是学习率(a),另外两个是一次momentum系数B1为0.9,B2为0.999
现在多数的研究人员都喜欢Adam
2、权重初始值
01 权重初始值不能是0
02 隐藏层激活值得选择
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def ReLU(x):
return np.maximum(0, x)
def tanh(x):
return np.tanh(x)
input_data = np.random.randn(1000, 100) # 高斯分布随机生成1000个数据
node_num = 100 # 各隐藏层的节点(神经元)数
hidden_layer_size = 5 # 隐藏层有5层
activations = {} # 激活值的结果保存在这里
x = input_data
for i in range(hidden_layer_size):
if i != 0:
x = activations[i-1]
# 改变初始值进行实验!
# w = np.random.randn(node_num, node_num) * 1
# w = np.random.randn(node_num, node_num) * 0.01
# w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num)
w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num)
a = np.dot(x, w)
# 将激活函数的种类也改变,来进行实验!
z = sigmoid(a)
# z = ReLU(a)
# z = tanh(a)
activations[i] = z
# 绘制直方图
for i, a in activations.items():
plt.subplot(1, len(activations), i+1)
plt.title(str(i+1) + "-layer")
if i != 0: plt.yticks([], [])
# plt.xlim(0.1, 1)
# plt.ylim(0, 7000)
plt.hist(a.flatten(), 30, range=(0,1))
plt.show()
03 relu的权重初始值
总结:
当激活函数使用relu时候,权重初始值使用He初始值,当激活函数为sigmoid或者tanh等S型曲线函数时候,初始值使用Xavier初始值。