谱卷积的GNN原理解释(Spectral Network),附代码
谱卷积的GNN原理解释(Spectral Network)
写在最前面:基于谱分解的GNN一般都认为来自Kipf大佬的论文: Semi-supervised classification with graph convolutional networks。其实在那之间,【1】早在14年就提出了Spectral的想法,但是此文发表后并没有得到大家的重视,直到Kipf对其进行了简化,谱方法才蓬勃发展开来。后边许多文章都从Kipf这篇文章获得了灵感。但是由于这篇文章的理解需要建立在很深的数学功底之上,并且其中的变换方法是比较抽象的。所以,我们再重温一遍论文里所涉及到的数学知识,希望能够对Spectral Network有一个更为深刻的理解。由于本人的数学比较渣,所以文章难免会出现差错,也欢迎各位大佬批评指正。
欧与非欧:谱方法到底在干什么
学过数据结构的都知道,一共有三种数据结构:线性表,树,图。与传统CNN中的网格状(grid-like)图像不同,GNN里的图都是没有规律可言的非欧式结构,因此并不具有平移不变性,因此无法应用CNN中的特定size的卷积核对其进行特征提取。
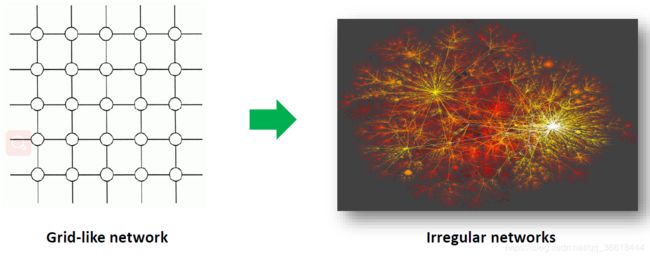
所以,机智的科学家们就想到,能不能将非欧式空间的图结构投影到欧式空间,再对投影之后的空间内的数据进行卷积,卷积之后的结果再还原到原来的空间呢?可!谱方法的思想由此诞生。
广义卷积:是一种数学运算
一提到卷积,我们可能首先会想到CNN里的卷积,其实这只是在函数是离散情况下的卷积,其定义为:

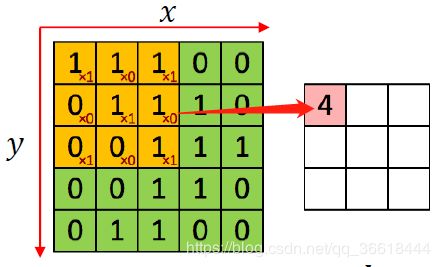
其中,f就是原函数,表示了矩阵x;g就是卷积核,其直观的表述如下:
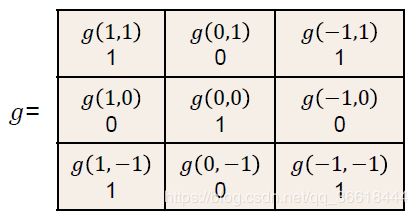
对于连续函数的卷积,则定义为乘积的积分:
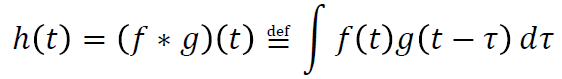
卷积的本质是乘法运算。卷积之后的函数相比于原函数更加平滑,这也是信号处理中滤波器的原理。
谱方法的具体操作
给出一个Network,拉普拉斯矩阵
![]() 描述了图最初始的拓扑特征。根据拉普拉斯矩阵的性质可以知道:拉普拉斯矩阵是半正定的对称矩阵,并且可以分解成一组特征向量U。因此拉普拉斯矩阵可以变换为:
描述了图最初始的拓扑特征。根据拉普拉斯矩阵的性质可以知道:拉普拉斯矩阵是半正定的对称矩阵,并且可以分解成一组特征向量U。因此拉普拉斯矩阵可以变换为:

其中,U是特征向量的矩阵,中间那个符号是特征值组成的对角矩阵。
使用U作为傅里叶变换的基底,将原特征投影到谱域里。(关于傅里叶变换的内容可以参考:https://blog.csdn.net/lzzdflg/article/details/78254381)。为了方便解释还是列几个公式:
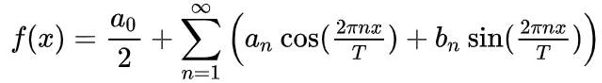
这里可以很清楚地看到,周期函数可以分解为一堆周期函数的叠加。而在实际操作中往往少有周期函数的情况,并且函数是离散的,为此把短暂的周期设置为无限大,那么其中的一个变换操作就会相当于在很短的周期内完成,离散便可以近似地看作是连续;而且非周期的问题也可以解决。经过一系列的推导,最终获得我们常用的傅里叶变换: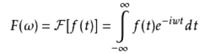 其中
其中![]() 表示傅里叶变换的基(欧拉公式将其变为虚数空间),而基就表示着我们经常谈起的“频域”的规律特征。频域的规律变换特征在时域上拉长就成了周期性的波。
表示傅里叶变换的基(欧拉公式将其变为虚数空间),而基就表示着我们经常谈起的“频域”的规律特征。频域的规律变换特征在时域上拉长就成了周期性的波。
如此一来图中顶点的特征在这组基底下被转换为
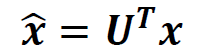 其中U的转置就是图上的傅里叶变换,那么傅里叶变换的逆变换就变为:
其中U的转置就是图上的傅里叶变换,那么傅里叶变换的逆变换就变为:![]() 根据卷积定理,两个信号的卷积的傅里叶变换是它们的傅里叶变换的点积,将GNN的卷积定义为:
根据卷积定理,两个信号的卷积的傅里叶变换是它们的傅里叶变换的点积,将GNN的卷积定义为:

其中,y是卷积核函数,为了对已经投射到谱域(傅里叶变换之后)里特征进行卷积,所以也要对卷积函数进行投影。卷积之后再进行傅里叶变换的逆变换,就将结果又带回了原来的空间。我们把卷积核的定义改写一下,使得式子变得更简单:

最终就得到了论文中提到的卷积方法了,其中gθ就是卷积函数了。这也是【1】所提到的操作。但是,到这里为止,还是有很大的弊端:
- 拉普拉斯矩阵十分费力,尤其是当网络规模太大(比如社交网络)的时候。
- 与傅里叶基底相乘的事件复杂度太高,而且变到谱域之后还得变回来。
- 信息更新来自所有结点,而不是本地邻居。
所以Kipf就做了如下的简化。
基于切比雪夫不等式截断的简化
论文中给出的原始的卷积计算方式的时间复杂度是 ![]() 此外拉普拉斯矩阵的特征分解的计算量也很大。文章Hammond et al.(2011) :Wavelets on graphs via spectral graph theory给出谱卷积可以很好的通过Chebyshev多项式
此外拉普拉斯矩阵的特征分解的计算量也很大。文章Hammond et al.(2011) :Wavelets on graphs via spectral graph theory给出谱卷积可以很好的通过Chebyshev多项式![]() 的K-th阶截断展开来拟合:
的K-th阶截断展开来拟合:
![]()
其中的数学原理请大家移步http://www.360doc.com/content/19/0310/08/53229185_820445844.shtml。因此论文定义特征向量对角矩阵的切比雪夫多项式为滤波器,也就是:
![]()
其中![]() 是缩放后的特征向量矩阵,缩放后范围是[−1,1] ,缩放的目的是为了满足Chebyshev多项式截断展开的条件:自变量范围需要在[−1,1]之间。
是缩放后的特征向量矩阵,缩放后范围是[−1,1] ,缩放的目的是为了满足Chebyshev多项式截断展开的条件:自变量范围需要在[−1,1]之间。![]() 是最大特征值,也叫谱半径。
是最大特征值,也叫谱半径。
Kipf大佬在这里还是觉得比较麻烦,所以他假设![]() ,如此一来卷积就升级为:
,如此一来卷积就升级为:
![]()
同时为了避免重复使用算子![]() 导致梯度爆炸或者梯度消失,又进行了renormalization trick操作,
导致梯度爆炸或者梯度消失,又进行了renormalization trick操作,![]() 其中
其中![]() 。
。
最终有了以下的定义:
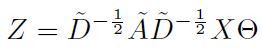
Θ是滤波器的参数矩阵,X是图结点的特征,前面那一大堆就是卷积。最后公式就变得十分类似我们常见的神经网络的propagation rule:
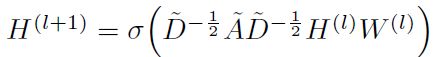
这也是论文最开始给出的公式。由此,层与层之间的传递关系就此定义,而这个复杂的、变态的进化过程最终把繁琐的数学概念赋予了超级直观的解释:下一层H(l+1)的状态受到H(l)的影响,通过学习参数矩阵W(l)我们得到最终的GNN。
就实验结果来说,GCN的效果要好于ChebyNet,那是因为ChebyNet允许许多高频的波形通过,而GCN只允许K=0(水平波)和K=1两类低频滤波器通过(low-pass filter),这使得GCN filter处理过的信号更为平滑,这更适用于结点分类的任务。
代码
如下是图卷积的一个简单实现,其核心步骤就是特征X与权重W的相乘,再用处理好的拉普拉斯矩阵与其相乘,返回值是在图上进行一次卷积之后的结果。对于GCN,需要进行两次图卷积。
class GraphConvolution(nn.Module):
def __init__(self, input_dim, output_dim,
dropout=0.,
is_sparse_inputs=False, # 输入的是不是稀疏矩阵
bias=False,
activation = F.relu,
featureless=False): # 都是有feature的所以不要更改
super(GraphConvolution, self).__init__()
self.bias = bias
self.activation = activation
self.is_sparse_inputs = is_sparse_inputs
self.featureless = featureless
self.weight = nn.Parameter(torch.randn(input_dim, output_dim))
self.bias = True
if bias:
self.bias = nn.Parameter(torch.zeros(output_dim))
def forward(self, x, support):
# convolve
xw = torch.matmul(x, self.weight) #matmul让不同维度矩阵相乘,得到【batch*nodes*out_dim】
out = torch.bmm(support, xw) # batch矩阵乘法,后两个维度相乘
if self.bias is not None:
out += self.bias
return self.activation(out)
总结
最后这个原始的粗糙的模型的一大堆缺点我就不再赘述了。由于许多后续的研究工作都是建立在这个基础上的,透彻的理解是十分、十分必要的。你不得不感叹学者们的智慧,并且你也要有一个深刻的教训:学好数学是十分必要的。
下个帖子可能做一些源代码的分享,下次见。
【1】J. Bruna, W. Zaremba, A. Szlam, and Y.LeCun. Spectral networks and locally connected networks on graphs. ICLR, 2014.