LU分解
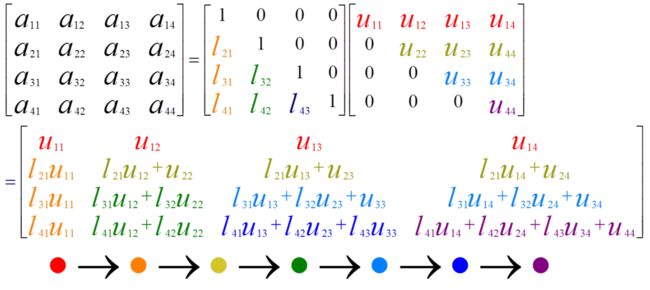
LU分解:将矩阵A分解成一个下三角矩阵L和一个上三角矩阵U的乘积 A=LU,称为对矩阵A的LU分解。
LU分解代码:
import numpy as np
def my_LU(b):
a = np.array(b)
n = len(a)
L = np.zeros([n,n])
U = np.zeros([n,n])
for k in range(n-1):
#选取a的第k列
gauss_vector = a[:,k]
#print(gauss_vector)
#求第k+1行往后的值
gauss_vector[k+1:] = gauss_vector[k+1:]/gauss_vector[k]
gauss_vector[0:k+1] = np.zeros(k+1)
L[:,k] = gauss_vector
L[k,k] = 1.0
#求第i行的值,用于求U矩阵
for i in range(k+1,n):
b[i,:] = b[i,:] - gauss_vector[i]*b[k,:]
a = np.array(b)
L[n-1,n-1] = 1.0
U = a
print(L)
print('*'*40)
print(U)
print('*'*40)
#验证LU分解成立
print(np.dot(L,U))
if __name__ == '__main__':
c = np.array([[2.,2.,3.],[4.,7.,7.],[-2.,4.,5.]])
my_LU(c)
LU分解求逆矩阵:
import numpy as np
import scipy
from scipy import linalg
#LU分解
a = np.array([[6., 2., 1., -1.], [2., 4., 1., 0.], [1., 1., 4., -1.], [-1., 0., -1., 3.]])
#LU分解
df = scipy.linalg.lu(a)
l = df[1]
u = df[2]
print(l)
print(u)
b1 = np.array([[1.], [0.], [0.],[0.]])
b2 = np.array([[0.], [1.], [0.],[0.]])
b3 = np.array([[0.], [0.], [1.],[0.]])
b4 = np.array([[0.], [0.], [0.],[1.]])
#分别求四个列向量
y1 = np.dot(np.linalg.inv(l),b1)
x1 = np.dot(np.linalg.inv(u),y1)
y2 = np.dot(np.linalg.inv(l),b2)
x2 = np.dot(np.linalg.inv(u),y2)
y3 = np.dot(np.linalg.inv(l),b3)
x3 = np.dot(np.linalg.inv(u),y3)
y4 = np.dot(np.linalg.inv(l),b4)
x4 = np.dot(np.linalg.inv(u),y4)
print(x1)
print("*" * 20)
print(x2)
print("*" * 20)
print(x3)
print("*" * 20)
print(x4)
print("*" * 20)
print(np.linalg.inv(a))