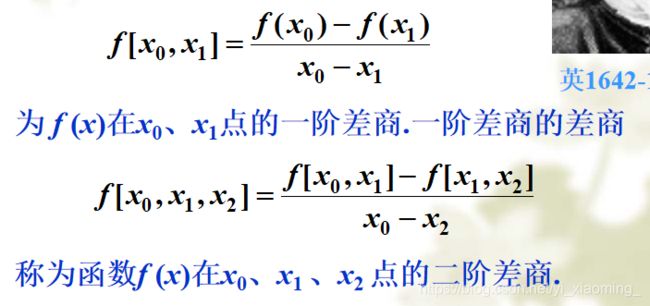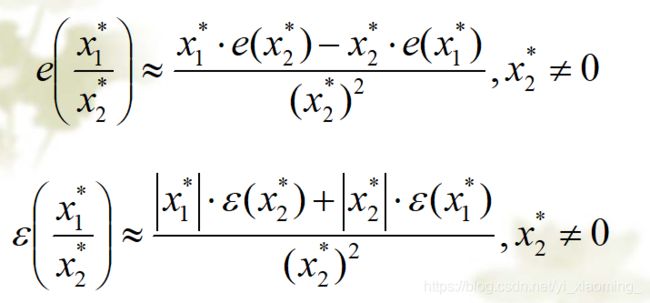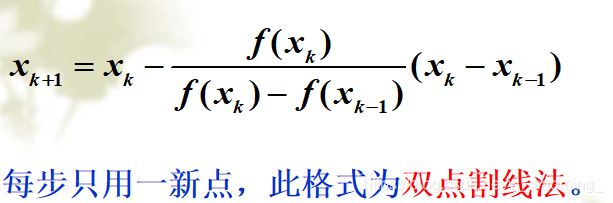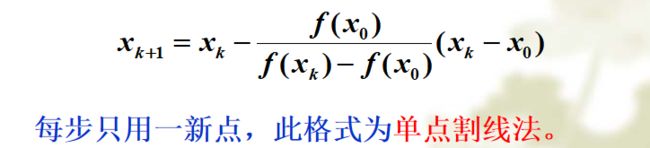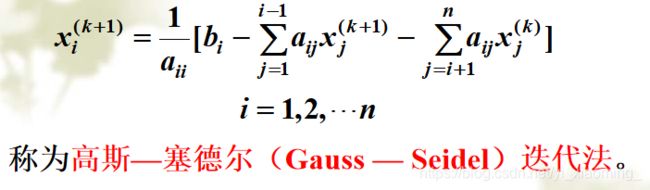数值计算方法
第一章 绪论
1.1 数值计算方法的研究对象和特点
1.计算机解决科学计算问题的一般过程可概括为:实际问题->数学模型->计算方法->程序设计->上机计算。
2.对算法所要考虑的问题:
a.计算速度:eg:求解一个20 阶线性方程组,用克莱姆法则要进行9.71020 次运算, 如用每秒1亿次乘法运算的计算机要30 万年; 而用加减消元法需3000 次乘法运算.
b.存储量
c.数值稳定性
3.数值计算方法的特点
面向计算机,算法只能包括加、减、乘、除运算和逻辑运算。
有可靠的理论分析,能任意逼近并达到精度要求,保证收敛性和数值稳定性,对误差进行分析。
有好的计算复杂性,时间复杂性和空间复杂性。
要有数值实验,通过数值试验证明是可行的。
1.2 浮点数
1.2.1 定点数
1.设r为大于1的正整数,ai为0,1,…,r-1中的某一个,位数有限的r进制正数可写成: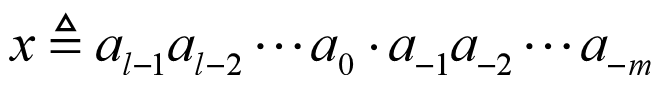
x有l位整数,有m位小数,因为进位制的基数是r,所以
![]()
把小数点永远固定在指定位置上位数有限的数称为定点数,称n=l+m为字长,一般取l=n,m=0或l=0,m=n.
2.值得指出 的是,在定点数运算操作数在它所能表示的范围内,而且还要求运算结果也在它所能表示的范围内,否则会产生溢出。
1.2.2 浮点数
1.设s是r进制数,p是r进制正负整数或零, r进制数x可以用s和rp的乘积表示为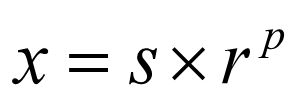
再设s的整数部分等于零,即s满足条件 -1
如果尾数的小数位数等于有限正整数t,则把x称为t位浮点数.
此外,如果还要求尾数s小数点后第一位数字不等于0,也就是要求尾数s满足条件 ,
,
则该浮点数为r进制规格化浮点数.
1.2.3 计算机数系
1.进位制为r, 阶数为p且l≤p ≤u,(l,u为整数), 尾数的小数位数为t, T位r进制浮点数集合F具有如下形式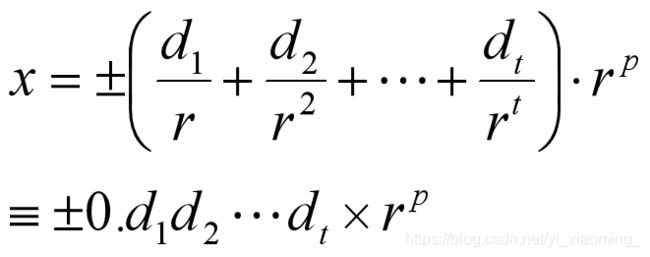
其中,di为整数满足0 ≤ di ≤r-1, i=1,2,…,t
F为规格化的浮点数系,F中共有2(r-1)rt-1(u-l+1)+1个浮点数.
2.任一计算机只能用有限的位数来表示浮点的尾数和阶数.
在计算机数系中,数的个数有限,数系中的每一个数都是有理数,从整体看,数系中的数分布很不均匀;
从局部看,阶数相同的数,又以相等的距离,分布在数轴的某一段上.
所以计算机数系是由一些残缺不全,分布不均匀的数组成,如果运算超出了计算机数系的范围,则产生溢出.
1.3 误 差
- 模型误差:在建立数学模型过程中, 不可能将所有因素均考虑, 必然要进行必要的简化, 这就带来了与实际问题的误差。
- 观测误差: 测量已知参数时, 受测量工具及手段的影响,测量数据带来的误差。
- 截断误差: 在数学模型不能得到精确解时,通常要用数值方法求它的近似解,其近似解与精确解之间的误差称为截断误差或方法误差。
- 舍入误差: 计算机的字长是有限的, 每一步运算均需四舍五入, 由此产出的误差。
- 误差和误差限

- 相对误差和相对误差限


7.有效数字:如果近似值x* 的误差限是其某一位的半个单位, 该位到x的第一位非零数字共有n 位, 我们称x有n 位有效数字。
8.
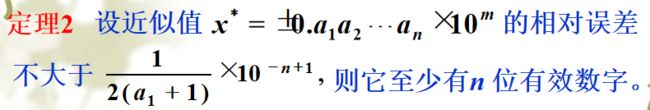
1.4 误差的传播
1.5 设计算法时应注意的原则
1.简化计算步骤, 减少运算次数。
2.注意避免两个相近数的相减,两个相近的数相减, 有效数字会大大损失。
3.防止大数 “吃掉” 小数。
4.避免除数的绝对值远小于被除数的绝对值。否则舍入误差会扩大。
5.使用数值稳定的算法。在运算过程中,舍入误差能控制在某个范围内的算法称为数值稳定的算法,否则就称为不稳定的算法.
第2章 方程求根
2.1 增值寻根法与二分法
1.
2.二分法,先求迭代次数

3.二分法的优点是简单,对f(x)只要求连续,它的收敛速度与比值为1/2的等比级数相同,它的局限性是只能用于求实根,不能用于求复根及公偶数重根.
2.2 迭代法
迭代法是一种逐步逼近的方法,它是解代数方程、超越方程、微分方程等的一种基本而重要的数值方法。
1.
2.4 牛顿切线法
解非线性方程f(x)=0的牛顿(Newton) 法,就是将非线性方程线性化的一种方法。它是解代数方程和超越方程的有效方法之 一。
1.![]()
2.5 割线法
第3章 线性方程组的数值方法
数值计算方法可求解线性代数方程组大致可分两类:
直接法,就是经过有限步算术运算,可求得方程组精确解的方法(如果每步计算都是精确进行的话)
迭代法,就是用某种极限过程逐步逼近其精确解的方法。
3.1.1 回代过程
1.若计算过程中没有舍入误差,经过有限次的算术运算,可求得方程组 Ax=b (|A|0)的精确解的方法叫直接法。主要用于解系数矩阵是低阶稠密矩阵的线性方程组。
2.
3.1.2 消元过程
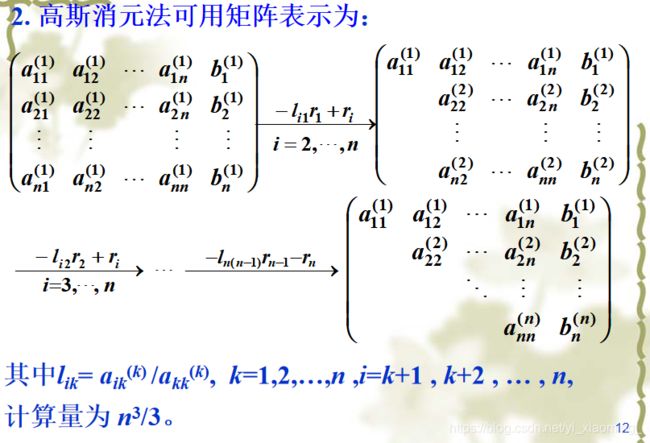
2.
3.从消元过程可以看出,对于n阶线性方程组,只要各步主元素不为零,经过n-1步消元,就可以得到一个等价的系数矩阵为上三角形阵的方程组,然后再利用回代过程可求得原方程组的解.
Ax=b 可用高 斯消元法求解的充分必要条件是:系数矩阵 A 的各阶顺序主子式均不为零。
4.当n较大时,高斯消元法中乘除法的次数与加减法的次数近似为![]()
3.2 高斯主元素消元法
1.在采用高斯消元法解方程组时,用做除法的小主元素可能使舍入误差增加,主元素的绝对值越小,则舍入误差影响越大。固应避免采用绝对值小的主元素,同时选主元素尽量的大,可使该法具有较好的数值稳定性。
2.列主元素消元法
3.完全主元素消元法 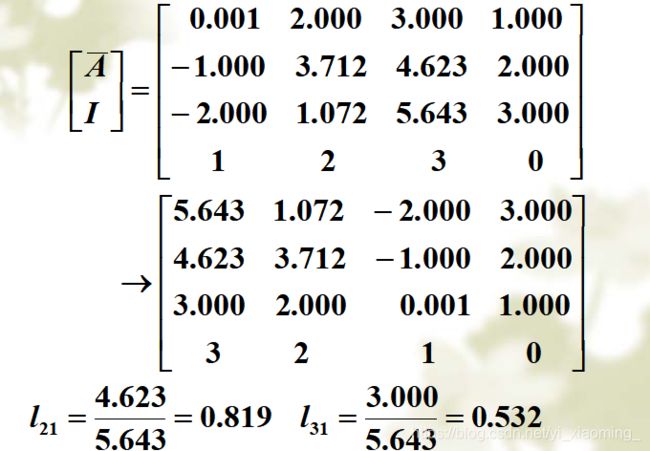
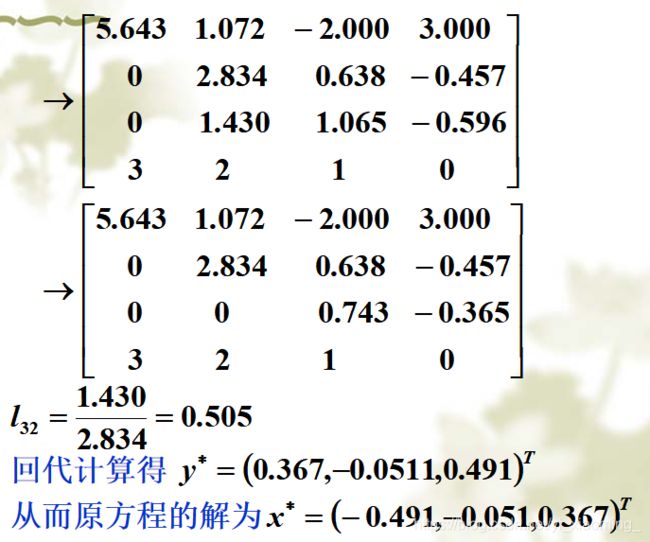
3.3 高斯——若当消元法
1.在高斯消元过程中,先将主元素化为1,而后将主元所在列的其它元素均化为零,最后将系数矩阵化为单位矩阵 E,无需回代就可求得原方程的解,此法称为高斯—若当消元法。
2.高斯—若当消元法也可进行全主元素消元法及列主元素消元法.
当值较大时,高斯消元法比高斯—若当消元法节省n3/6次乘除法和加减法。
3.高斯—若当消元法对求 一个矩阵的逆矩阵,或对求解仅常数项不同的很多方程组及矩阵方程是非常有用的.
3.4 矩阵分解
3.5 向量与矩阵的范数
1.
2.对任意 n 维向量 x∈Rn,若对应非负实数 ||x|| , 满足
① 非负性 ||x||≥0 ,等号仅当 x=0 时成立;
② 齐次性 对任何实数 λ , || λ x||=| λ |· ||x||;
③ 三角不等式 ||x+y||≤ ||x|| +||y|| ;
则称 ||x|| 为向量 x 的范数。
3.

4.矩阵的范数

5.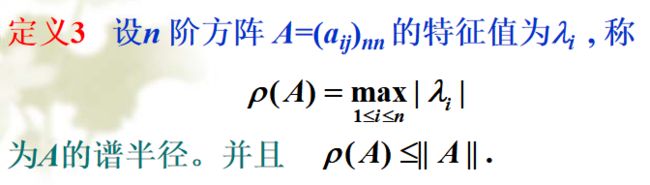
3.6 误差分析
3.7 迭代法及其收敛性
3.8 雅可比迭代法与高斯—塞德尔迭代法
第4章 矩阵的特征值与特征向量问题
对n 阶方阵A求数λ和非零向量x ,使其满足Ax=λx这样的 λ 值称为矩阵A的特征值,非零向量 x 称为矩阵A的与特征值λ 相对应的一个特征向量。
4.1 幂法与反幂法
1.矩阵按模最大的特征值称为主特征值,幂法是计算矩阵的主特征值和相应特征向量的一种向量迭代法。
2.幂法;
3.幂法的加速:原点平移法
4. 反幂法是用于求非奇异矩阵A的按模最小的特征值和对应特征向量的方法. 而结合原点平移法的反幂法则可以求矩阵A的任何一个具有先验了解的特征值和对应的特征向量。
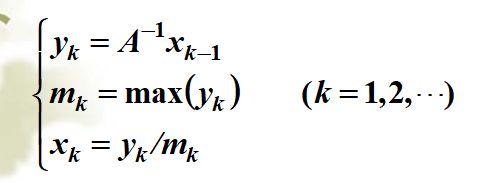
第5章 代数插值
5.1 插值多项式的存在唯一性
5.2 拉格朗日插值多项式
1.基函数



2.插值余项:截断误差Rn(x)=f (x) -Ln(x)也称为插值多项式的余项。
3.拉格朗日余项定理:
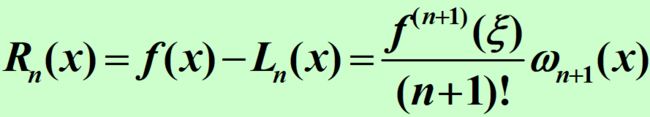
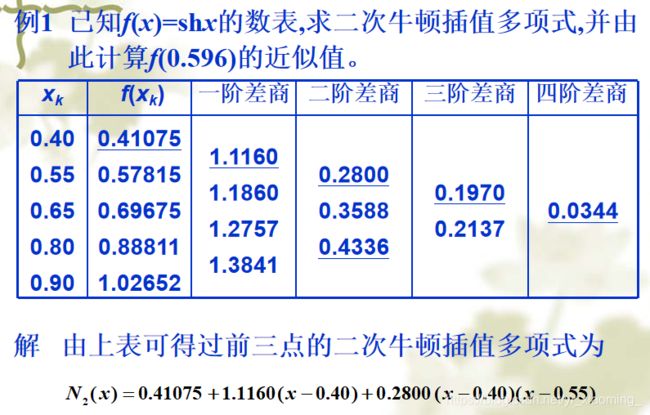
5.3 牛顿插值多项式
拉格朗日插值的优点是插值多项式特别容易建立,缺点是增加节点时原有多项式不能利用,必须重新建立,即所有基函数都要重新计算,这就造成计算量的浪费
牛顿插值多项式是代数插值的另一种表现形式,当增加节点时它具有所谓的”承袭性”,这要用到差商的概念。
1.