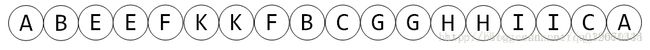DFS序——树链剖分前驱知识
目录
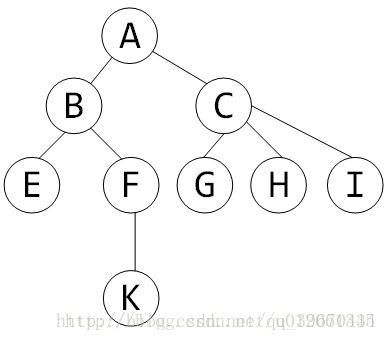
定义:dfs序:每个节点在dfs深度优先遍历中的进出栈的时间序列。
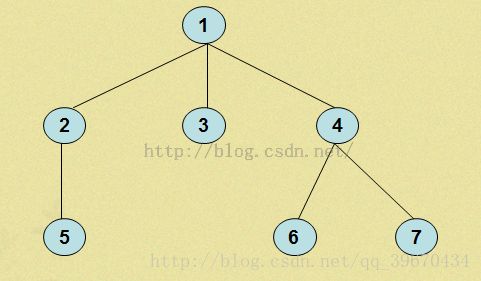
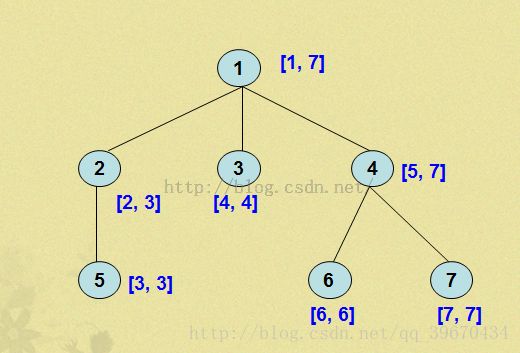
性质:dfs序可以把一棵树区间化,即可以求出每个节点的管辖区间。
对于一棵树的dfs序而言,同一棵子树所对应的一定是dfs序中连续的一段。
dfs序的七个基本问题:
定义:dfs序:每个节点在dfs深度优先遍历中的进出栈的时间序列。
定义两个数组,in[x],out[x]。dfs从根结点开始,每个结点分别记录两个信息:in[x],out[x],in[x]为dfs进入结点x时的时间戳,out[x]为dfs离开结点x时的时间戳。
dfs序的基本代码:
void dfs(int x,int pre,int d){//L,R表示一个子树的范围 L[x]=++tot; dep[x]=d; for(int i=0;i
性质:dfs序可以把一棵树区间化,即可以求出每个节点的管辖区间。
对于一棵树的dfs序而言,同一棵子树所对应的一定是dfs序中连续的一段。
dfs序的七个基本问题:
ps:deep[x]为x的深度,l[x]为dfs序中x的位置,r[x]为dfs序中x子树的结束位置
1.点修改,子树和查询
在dfs序中,子树处于一个连续区间中。所以这题可以转化为:点修改,区间查询。用树状数组或线段树即可。
例:poj3321 Apple Tree
链接:邻接表数组实现详解
//dfs序+树状数组
#include
#include
#include
#include
using namespace std;
const int N = 500005;
struct Edge{ //邻接表——数组实现 (链式前向星)
int to,next;
}edge[N];
int head[N],tot,d[N];
int in[N],out[N]; //in[i]:dfs第一次进入顶点i的时间戳,in[i]为dfs离开该节点的时间戳
bool have[N];
int cnt;
void init(){
tot = 0;
cnt = 0;
memset(head,-1,sizeof(head));
memset(d,0,sizeof(d));
}
void addEdge(int u,int v,int &k){
edge[k].to = v;
edge[k].next = head[u]; //edge[k].next存储的是编号为i的边的(同样以u为起始点的)前一条边的编号
head[u] = k++; //最后一条以u为起始点的边的编号
}
void dfs(int u){ //dfs序
in[u] = ++cnt;
for(int k=head[u];k!=-1;k=edge[k].next){
dfs(edge[k].to);
}
out[u] = cnt;
}
int lowbit(int x){
return x&(-x);
}
int sum(int x){
int res = 0;
while(x){
res+=d[x];
x-=lowbit(x);
}
return res;
}
void update(int x,int v){
while(x<=cnt){
d[x]+=v;
x+=lowbit(x);
}
}
int main()
{
int n,m;
while(scanf("%d",&n)!=EOF){
init();
for(int i=0;i 2.树链修改,单点查询
将一条树链x,y上的所有点的权值加v。这个问题可以等价为:
1).x到根节点的链上所有节点权值加v。
2).y到根节点的链上所有节点权值加v。
3).lca(x,y)到根节点的链上所有节点权值和减v。
4).fa(lca(x,y))到根节点的链上所有节点权值和减v。
上面四个操作可以归结为:节点x到根节点链上所有节点的权值加减v。修改节点x权值,当且仅当y是x的祖先节点时,x对y的值有贡献。
所以节点y的权值可以转化为节点y的子树节点贡献和。从贡献和的角度想:这就是点修改,区间和查询问题。
修改树链x,y等价于add(l[x],v),add(l[y],v),add(l[lca(x,y)],-v),add(l[fa(lca(x,y))],-v)。
查询:get_sum(r[x])-get_sum(l[x]-1)
用树状数组或线段树即可。
3.树链修改,子树和查询
树链修改部分同上一问题。下面考虑子树和查询问题:前一问是从贡献的角度想,子树和同理。
对于节点y其到根节点的权值和,考虑其子节点x的贡献:w[x]*(deep[x]-deep[y]+1) = w[x]*(deep[x]+1)-w[x]*deep[y]
所以节点y的子树和为:
ps:公式中的v[i]为手误,应为w[i]。
所以用两个树状数组或线段树即可:
第一个维护∑w[i]*(deep[i]+1):支持操作单点修改,区间和查询。(这也就是问题2)
第二个维护∑ w[i]:支持操作单点修改,区间查询。(这其实也是问题2)
4.单点更新,树链和查询
树链和查询与树链修改类似,树链和(x,y)等于下面四个部分和相加:
1).x到根节点的链上所有节点权值加。
2).y到根节点的链上所有节点权值加。
3).lca(x,y)到根节点的链上所有节点权值和的-1倍。
4).fa(lca(x,y))到根节点的链上所有节点权值和的-1倍。
所以问题转化为:查询点x到根节点的链上的所有节点权值和。
修改节点x权值,当且仅当y是x的子孙节点时,x对y的值有贡献。
差分前缀和,y的权值等于dfs中[1,l[y]]的区间和。
单点修改:add(l[x],v),add(r[x]+1,-v);
5.子树修改,单点查询
修改节点x的子树权值,在dfs序上就是区间修改,单点权值查询就是单点查询。
区间修改,单点查询问题:树状数组或线段树即可;
6.子树修改,子树和查询
题目等价与区间修改,区间查询问题。用树状数组或线段树即可。
7.子树修改,树链查询
树链查询同上,等价为根节点到y节点的链上所有节点和问题。
修改节点x的子树权值,当且仅当y是x的子孙节点时(或y等于x),x对y的值有贡献。
x对根节点到y节点的链上所有节点和的贡献为:w[x]*(deep[y]-deep[x]+1)=w[x]*deep[y]-w[x]*(1-deep[x])
同问题三,用两个树状数组或线段树即可。
参考文章:树 DFS序 详解[完全版]
初学dfs序
DFS序详解
dfs序的七个基本问题来源如下
作者:weeping
出处:www.cnblogs.com/weeping/
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。