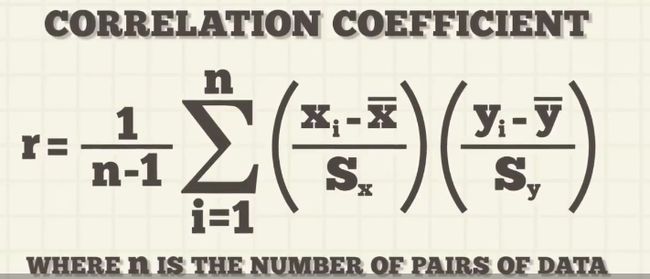关于协方差与相关系数
今天突然看到协方差这个概念,又熟悉又陌生,只是朦朦胧胧知道这个可以反映出两个随机变量之间的相关性,但是对其内在原理不理解,不知道协方差需要随机变量满足什么形式后才可以用协方差计算,或许说,怎么将协方差应用于数据上,并且得到相应的分析结果。
经过我一通百度,终于有点明白协方差是说什么意思了,感觉很久没有理解过数学了,所以很想分享一下这次的理解。
假如有两个随机变量 X,Y ,且X的数学期望是E(X), Y的数学期望是E(Y)
我们就把 E[X-E(X))*(Y-E(Y)] 叫做协方差
由于挺久没接触了,一看这条公式我也蒙了,不过详细看,会发现有几个有趣的点
- 如果X=Y, 那么协方差其实就是这个数的方差
E[(X-E(X))**2] - 如果X Y相互独立,那么协方差就会等于0,这是因为
E[X-E(X))*(Y-E(Y)] = E[X*Y] - E[X]*E[Y],如果相互独立,那么E[X*Y] = E[X]*E[Y],协方差就自然等于0了
从这两点我们可以发现,协方差至少可以反映两个潜在因素 1. 随机变量自身的扰动误差(方差) 2. 随机变量之间的相关性(联系)
首先从定义入手,对于离散的随机变量,协方差的计算就是 1/N * (X1-E[X])*(Y1-E[Y]) + (X2-E[X])*(Y2-E[Y]) +....
- 如果 X Y数据自身比较平稳,偏离误差小,那么
(X1-E[X])*(Y1-E[Y])的计算值是比较小的,所以协方差较小,极端情况是两个常数,数据无误差无偏离,那么协方差就必然为0,协方差可以体现出X Y两个随机变量自身数据的偏离程度。 - 如果X,Y数据自身十分震荡,那么协方差就一定会大吗? 答案是不一定的,因为协方差是同时被两个因素所影响,一个是数据偏离程度和数据相关性,两个随机变量之间不怎么相关,那么协方差是趋向于0的
IF X-E[X] > 0, AND Y-E[Y] > 0 (1)
IF X-E[X] < 0, AND Y-E[Y] > 0 (2)
IF X-E[X] > 0, AND Y-E[Y] < 0 (3)
IF X-E[X] < 0, AND Y-E[Y] < 0 (4)
协方差的计算中可能出现以上四种情况,我们分情况来讨论:
- 如果1式和4式出现的情况比较多,也就是如果X比较大的时候,Y也比较大-(1),X比较小的时候,Y也比较小(4), 而2,3式情况出现得很少,那么我们就觉得,X 和 Y 之间是相关的,虽然不一定线性相关,但是是存在相关关系的,而且还是正相关。
- 有了正相关就有负相关,比如X比较大的时候,Y比较小(3),X比较小的时候,Y比较大(2),如果这两种情况出现得比较多,那么就是负相关
- 如果正相关和负相关到极致了,也就是线性关系了,那么就只出现2种情况,也就是我们上述所说的。
- 不过也会出现第三种情况,也就是X比较大的时候,Y可能比较大,也可能比较小,X比较小的时候,Y可能比较大,也可能比较小,也就是上面四种情况出现的概率都几乎是一样的,这时候既不是正相关,也不是负相关,所以就是不相关。简单来讲,就是X怎么变化,都不影响Y。
- 从计算的角度上来看,如果四种情况出现的概率都相近的话,通过抵消,协方差也是趋向于0的,而正相关的协方差趋向于比较大的正数
X-E(X) * Y-E(Y) > 0,负相关趋向于比较大的负数,X-E(X) * Y-E(Y) > 0.
所以这就是为什么协方差可以度量出两个随机变量的相关性
不知道你有没有发现,协方差度量随机变量之间的线性关系的,这点很重要,对于函数关系,比如二次函数,协方差是无能为力的,因为协方差的计算很简单,就是通过正负关系的抵消或者累积。
不过,协方差较大的情况可以是数据偏离程度较大,也可能是两个变量相关性很强,该怎么分清楚呢?
于是就提出相关系数概念,注意,这个系数出现了相关的概念,意识就是相关系数可以代表相关性,不会混杂其他的,比如协方差为啥不叫相关差呢?就因为协方差不仅仅包括着相关性
相关系数一般指的是皮尔逊相关系数
相关系数取值为[-1,1] 1代表正相关的线性关系(强相关),-1代表负相关的线性关系(强相关),而0代表不相关,绝对值越大相关程度越大。
其实就是协方差除以各自标准差的乘积,如果两个数相同,那么相关系数就等于 方差/方差 就会等于1。协方差除以标准差可以约掉数字自身的误差偏离程度因素,使得相关系数仅仅反映变量之间的联系。
想象一个简单的情况,假设数字自身的误差偏离程度因素为A , 数据联系为B。协方差大约为A*B
那么相关系数大约为 A*B/A = B
接下来通过一些数据实验来证明一下我们的猜想
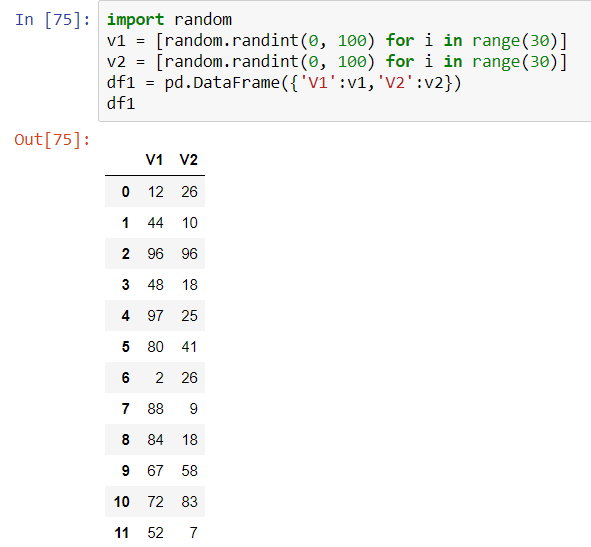
先生成两列数据,随机生成
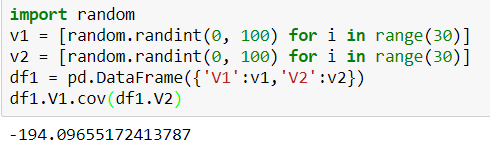
首先计算这两个的协方差
会发现特别大,因为这两个是随机生成的,基本无联系,且取值范围在100以内,数据很乱偏离程度大,所以协方差很大,如果取值在10以内,那么协方差将会少
明显小了好多,所以验证了我们的假设,协方差会被数据自身的偏离误差程度所影响
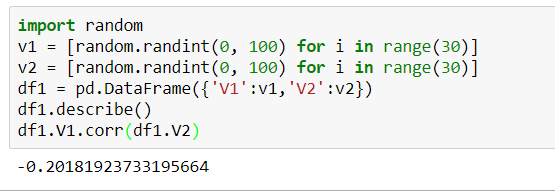
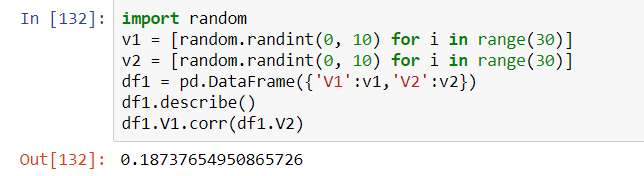
如果我们来计算这两个随机变量的相关系数,对比10和100
无论是10或者是100,相关系数都在小于0.3下波动,代表很弱的相关性,可以看出相关系数不由数据自身误差偏离影响,只反映随机变量之间的相关性
体现了两个随机变量之间的强相关,而且是负相关的线性关系的,-0.99999而不是等于1是由于计算机精度的问题。
为此,我们就解决了协方差的一些概念理解问题啦,一般我们可以用相关系数去度量两个变量之间的相关性,不过函数关系就无法用协方差来体现了
那如果两个变量之间存在其他关系,不是线性关系,无法用协方差来度量,那采取哪种方式?
我们可以用统计机器学习来解决这个问题,下次写