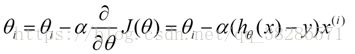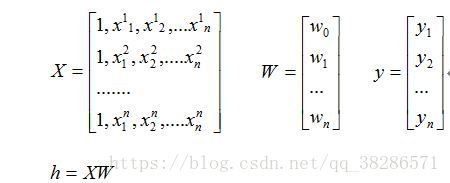线性回归（LinearRegression）实现房价预测

线性回归主要处理以连续型特征为主的数据集，线性回归函数为f(X) = bX+a，对于损失函数的建立主要使用的是最小二乘法，使用梯度下降法拟合线性模型，基本原理如下：
函数模型（model）：

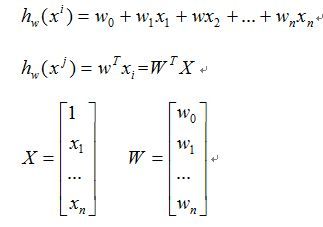
假设有训练数据

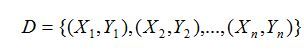
我们写成矩阵的形式为；

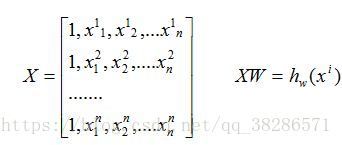
对于损失函数（cost）
现在我们需要根据给定的X求解W的值，这里采用最小二乘法， 何为最小二乘法，其实很简单。我们有很多的给定点，这时候我们需要找出一条线去拟合它，那么我先假设这个线的方程，然后把数据点代入假设的方程得到观测值，求使得实际值与观测值相减的平方和最小的参数。对变量求偏导联立便可求。
因此损失代价函数为：

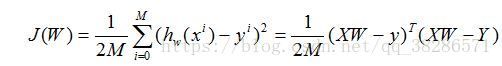
梯度下降算法求解：
现在我们的目的就是求解出一个使得代价函数最小的W：
a.矩阵满秩可求解时（求导等于0）

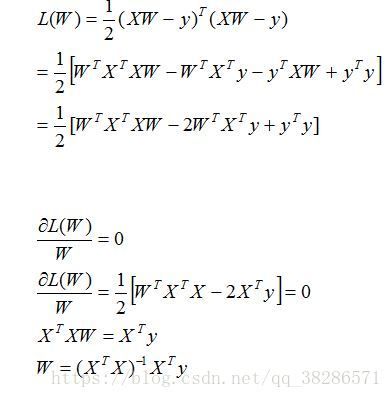
b.矩阵不满秩时（梯度下降）：
梯度下降算法是一种求局部最优解的方法，对于F(x)，在a点的梯度是F(x)增长最快的方向，那么它的相反方向则是该点下降最快的方向，具体参考wikipedia。 原理：将函数比作一座山，我们站在某个山坡上，往四周看，从哪个方向向下走一小步，能够下降的最快；注意：当变量之间大小相差很大时，应该先将他们做处理，使得他们的值在同一个范围，这样比较准确。
1）首先对θ赋值，这个值可以是随机的，也可以让θ是一个全零的向量。
2）改变θ的值，使得J(θ)按梯度下降的方向进行减少。描述一下梯度减少的过程，对于我们的函数J(θ)求偏导J；

假设有数据集D时：

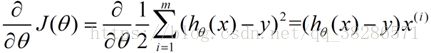
对损失函数求偏导如下：

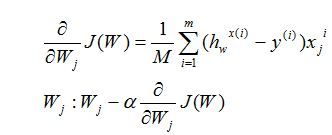
使用矩阵表示（方便计算）

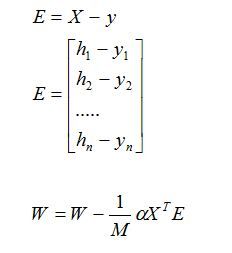
基本上每个模型都会有一个对应的目标函数，可以通过不同的最优化求解方法（梯度下降）对这些对应的目标函数进行求解。线性回归模型，我们知道实际上是通过多个自变量对自变量进行曲线拟合。我们希望找到一条可以较好拟合的曲线。

代码实现如下
1、首先使用线性回归算法最小二乘法实现预测

导入需要的python库

import numpy as np
import pandas as pd
import pylab

建立computer_error函数，构造误差函数 ∑_(i=1)^n▒〖(y-f(x))^2〗 使用最小二乘法求所有样本的离差值。代码如下：

def compute_error(a,b,data):
    totalError =0 #给定离差初值
    x = data[:,:-1]#利用切片获取数据集的前十三个特征值作为X
    y = data[:,-1]#获取样本的房价
    s = np.sum(b*x,axis=1) 
    totalError = (y-a-s)**2   #求离差 
    totalError = np.sum(totalError,axis=0)   #求所有离差的和
    totalError = totalError/float(len(data))#离差平均
    print('Error:',totalError)

2、建立优化函数，更新 f(X) = bX+a 函数的与a值与b值。

def  optimizer(data,starting_a,starting_b,learning_rate,num_iter):  #num_iter 迭代次数
    a = starting_a  #starting_ 初始值
    b = starting_b
    # 梯度下降
    for i in range(num_iter):
        # 朝梯度下降的方向更新a，b
        a,b =compute_gradient(a,b,data,learning_rate)
        if i%1000==0:#定义显示的迭代步数
            print('iter {0}:error={1}'.format(i,compute_error(a,b,data)))  #根据迭代次数输出离差值

3、建立梯度函数更新函数的a值与b值，

def compute_gradient(a_current,b_current,data,learning_rate):  #函数compute_gradient 对当前的a,b进行一次梯度迭代运算
    N = float(len(data)*10)
    x = data[:,:-1]
    y = data[:,-1]
    s = np.sum(b_current*x,axis=1) 
   # print('s = ',s)
    a_gradient = -(2/N)*(y-s-a_current)
   # print(a_gradient)
    a_gradient = np.sum(a_gradient,axis=0)  #axis=0 理解为将一组数据变成一个数据    
    cost = (y-s-a_current).reshape(len(data),1)
   # print(cost)
    b_gradient = -(2/N)*x*cost  #此处求出是正梯度
    #N用于量化迭代步骤，减少迭代次数

    b_gradient = np.sum(b_gradient,axis=0)
   #a与b值的更新迭代过程，每次迭代得到新的a与b传给函数。
    new_a = a_current - (learning_rate * a_gradient)  #- (learning_rate * a_gradient) 负梯度
    new_b = b_current - (learning_rate * b_gradient）

4、建立线性回归函数，读取数据，设定相应的参数并用于调参，其中包括梯度下降学习步长，a，b初始值，迭代次数。

def Linear_regression():  #Linear_regression 线性回归
    # 加载样本数据，读取data
    data=pd.read_excel('data.xls',)
    data=np.array(data)
    learning_rate = 0.00002#设置机器学习步长
    initial_a = 0.0
    k = len(data[:,:-1])
    initial_b = np.zeros((1,13))
    num_iter = 100000

    print('initial variables:\n initial_a = {0}\n intial_b = {1}\n error of begin = {2} \n'\        .format(initial_a,initial_b,compute_error(initial_a,initial_b,data))）
    [a ,b] = optimizer(data,initial_a,initial_b,learning_rate,num_iter)
    print('final formula parmaters:\n a = {1}\n b ={2}\n error of end = {3} \n'
          .format(num_iter,a,b,compute_error(a,b,data)))

完整的最小二乘法实现代码：

import numpy as np
import pandas as pd
import pylab
#定义函数参数a,b以及数据
#定义初始离差为0，通过x,y计算对其赋值
#返回
def compute_error(a,b,data):
    totalError = 0
    x = data[:,:-1]
    y = data[:,-1]
    s = np.sum(b*x,axis=1)
    totalError = (y-a-s)**2   #求离差    
    totalError = np.sum(totalError,axis=0)   #求所有离差的和
    totalError = totalError/float(len(data))
    print('Error:',totalError)
    return totalError#/float(len(data))   #求离差和的平均值；float：将数据个数（整数）化为辅点数

def optimizer(data,starting_a,starting_b,learning_rate,num_iter):  #num_iter 迭代次数
    a = starting_a  #starting_ 初始值
    b = starting_b
    # 梯度下降
    for i in range(num_iter):
        # 朝梯度下降的方向更新a，b
        a,b =compute_gradient(a,b,data,learning_rate)
        if i%1000000==0:
            print('iter {0}:error={1}'.format(i,compute_error(a,b,data)))  #迭代次数：离差
    return [a,b]

def compute_gradient(a_current,b_current,data,learning_rate):  #函数compute_gradient 对当前的a,b进行一次梯度迭代运算
    N = float(len(data)*10)
    x = data[:,:-1]
    y = data[:,-1]
    s = np.sum(b_current*x,axis=1) 
    a_gradient = -(2/N)*(y-s-a_current)  #此处求出是正梯度
    a_gradient = np.sum(a_gradient,axis=0)  #axis=0 理解为将一组数据变成一个数据    
    cost = (y-s-a_current).reshape(len(data),1))
    b_gradient = -(2/N)*x*cost  #此处求出是正梯度
    #N量化迭代步骤，减少迭代次数
    b_gradient = np.sum(b_gradient,axis=0)
    new_a = a_current - (learning_rate * a_gradient)  #- (learning_rate * a_gradient) 负梯度
    new_b = b_current - (learning_rate * b_gradient)
    return [new_a,new_b]

def Linear_regression():  #Linear_regression 线性回归
    # 加载样本数据
    data=pd.read_excel('data.xls',)
    data=np.array(data)
    #print(data)
    learning_rate = 0.00002
    initial_a = 0.0
    k = len(data[:,:-1])
    initial_b = np.zeros((1,13))
    print(initial_b)
   # n = len(data)
    #initial_b = tile(initial_b,(n,1))
    num_iter = 10000000
    print('initial variables:\n initial_a = {0}\n intial_b = {1}\n error of begin = {2} \n'\
        .format(initial_a,initial_b,compute_error(initial_a,initial_b,data)))

    [a ,b] = optimizer(data,initial_a,initial_b,learning_rate,num_iter)

    print('final formula parmaters:\n a = {1}\n b ={2}\n error of end = {3} \n'
          .format(num_iter,a,b,compute_error(a,b,data)))
if __name__ =='__main__':

    Linear_regression()

由于样本特征数过多，模型算法迭代比较慢，进行10000000步迭代后得到的b=[[-5.42817096e-02 3.59839620e-02 -2.36259578e-02 7.64642686e-01
1.79519737e-01 5.12378209e+00 7.32771368e-03 -6.31054419e-01
4.03647089e-01 -2.25624979e-03 -4.38944861e-01 1.39016104e-02
-4.99409372e-01]]

得到的a值为 a= 0.5256249660863571
error= 25.401445986356332

上面是使用基本算法实现，下面调用sklearn中的线性回归模型实现对房价的预测和评估。关于sklearn模块的一些介绍链接地址：http://scikit-learn.org/stable/modules/classes.html#module-sklearn.datasets。基本代码实现和讲解如下：

# -*- coding: utf-8 -*-
from sklearn import linear_model
from sklearn import cross_validation
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import math

def dataSet(src):
    data =np.array(data)
    features =data[:,:-1]#取出所以数据的前十三项作为特征值
    price = data[:,-1]  #取出数据的最后一项作为房价价格
    #对数据集进行训练集和测试集分割，训练集占60%，测试集占%40
    features_train,features_test,price_train,price_test=cross_validation.train_test_split(features,price,test_size=0.3,random_state=0)                                                                                           
    #print(features_train.shape,price_train.shape)
    return features,price 
    #模型可视化，用于评估预测价格与真实价格之间的误差，黄色点越接近绿色直线，说明预测价格更接近真实价格 
def show(price_test,predict_price):
    plt.plot( price_test,predict_price, color='y', marker='o')
    plt.plot(price_test, price_test,color='g', marker='+')
    plt.show()
    #导入线性回归模型训练数据集
data = pd.DataFrame(pd.read_excel('data.xls'))     
clf = linear_model.LinearRegression()
clf.fit(features_train,price_train)

#计算线性回归模型的斜率，总共有十三个features，所以求出的斜率有十三个，即y=x1*b1+x2*b2---x13*b13
w = clf.coef_
print("w = ",w)
b = clf.intercept_  #线性回归模型计算截距值
print("b = ",b)

R_Square = clf.score(features_train,price_train)  #判定系数R-Square,即描述模型和数据的拟合程度
#print(R_Square)

#使用features测试price，这里只列举了一个样本的特征进行价格的预测，实际值为41，得到的预测值为35.9
a=[[0.08187,    0,  2.89,   0,  0.445,  7.82,   36.9,   3.4952, 2,  276,    18,
    393.53, 3.57]]
predict_a = clf.predict(a)
print("predict_a=",predict_a)

#使用测试集评估模型,首先输入测试集features，得到预测的price
predict_price = clf.predict(features_test)
list(predict_price)  #预测价格生成列表
print(predict_price)

error_sum =sum(sqrt((price_test-predict_price)**2)) #求解预测price与真实price之间的误差总和
price_test_sum =sum(price_test)
error =error_sum/price_test_sum  #评估模型的准确度
print("accuracy=",accuracy)
show(price_test,predict_price)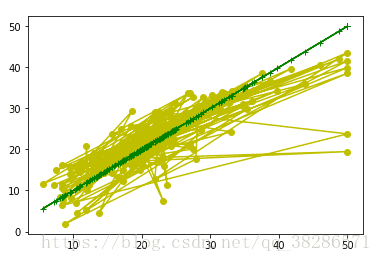

得到的评估图像如图，绿色点为真实价格，黄色点为测试集预测到的价格。根据距离绿色点的距离可以知道预测价格的偏离程度。
模型的输出误差error= 0.16403668101387084

源代码和数据链接地为：
https://pan.baidu.com/s/1hQW_fHi1rsghxrUCGknSlg