Integral Human Pose Regression ECCV 2018
Abstract:
用热点图表示pose的缺点
- 不可微分的后期处理 non-differentiable postprocessing
- 量化误差 quantization error
本篇文章用一个简单的积分运算联系并统一了热图表示和关键点回归,避免了上述问题。
对所有基于热图的方法都有效。实验证明各种环境下该方法的有效性,尤其是3D pose estimation。
Keywords:
Integral regression · Human pose estimation · Deep learning.
1 Introduction
human pose estimation 被广泛研究 。 [24, 3, 28] 使用CNN 在该问题上取得了显著进展。在二维姿态估计中,最好的方法都是基于检测的[2]。它们为每个关节生成一个可能性热图,并将该关节定位为图中最大可能点(maximum likelihood)。对热图进行了扩展,用于三维姿态估计,显示出良好的[37]性能。
尽管热图的性能出色,但是有着本质上的缺点,详见第二节。
姿态估计本质上是一个回归问题,产生连续输出的端对端回归方法可以解决以上问题。但是回归方法regression methios,不如基于检测的方法detection based methods有效。
2D pose benchmark [2] 中表现最好的方法只有[7]是基于回归的。
(原因可能是热图受到密集的像素监督 supervised by dense pixel information,更容易学习)
3D 姿态估计基于点归回的方法广泛应用,但效果不佳。[42, 55,56, 31, 32, 30, 35, 43, 21, 14],
现有的工作要么基于检测,要么基于回归。这两个范畴之间存在着明显的差异,对它们之间的关系研究甚少。本文表明,一个简单的操作就可以将热图表示和联合回归联系起来并统一起来。它将取最大值“taking-maximum”操作修改为取期望“taking-expectation”操作。关节被估计为热图中所有位置的积分,由它们的概率加权(从可能性归一化)。我们称这种方法为积分回归*integral regression。
它共享热图表示和回归方法的优点,同时避免了它们的缺点。
- 积分函数是可微的,允许端到端训练。
- 简单,在计算和存储方面带来的开销很小。
- 可以很容易地结合任何基于热图的方法。
integral 不是新事物,在 [27, 52, 45]中作为 soft-argmax出现,同期[29,34] 应用于 pose estimation。但是做的消融实验不足,没有体现出integral regression的有效性。
(只在性能饱和的2d benchmark MPII[2] 上做了性能测试)
由于 integral 无参数,只是转换 heat map 到 joint ,可以应用于任何算法设计。
可以结合不同的
- tasks,
- heat map and joint losses,
- network architectures,
- image and heat map resolutions.
主要贡献
在各种实验设置下应用积分回归并验证其有效性。具体来说,我们首先证明了积分回归显著提高了三维姿态估计,使三维和二维数据的混合使用成为可能,并在人3.6 m[24]上实现了最先进的结果。我们在2D位姿基准测试(MPII[3]和COCO[28])上的结果也很有竞争力
code:https://github.com/JimmySuen/integral-human-pose
2 Integral Pose Regression
基于热图的(based on heat map)方法
Input : learned heat map
- H k \boldsymbol{H}_k Hk for k t h k^{th} kth joint
Output: The final joint location coordinate
J k = arg max p H k ( p ) \boldsymbol J_k = \arg \max _\boldsymbol p \boldsymbol{H}_k(\boldsymbol p) Jk=argpmaxHk(p)
得到最大可能性的位置p。
基于热图方法的两大缺点
-
“取最大值taking-maximum”操作是不可微分的non-differentiable,并且阻止了端到端的训练。 只能对热图进行监督。
-
低分辨率热图,网络中下采样环节会造成量化误差 quantization errors,热图分辨率比输入分辨率低的多。 提高分辨率,虽然会提升精度,但是会造成计算和存储的高要求。
基于回归关键点(regression methods)的两大优点
- 端到端学习,推断和训练的目的一致。
- 输出是连续,理论上可以达到任意的定位精准度。(与heatmap中的量化误差相反)
提出了一种将热图转换为节点位置坐标的统一方法,从根本上缩小了热图与基于回归的方法之间的差距。它带来了原理和实用上的好处。将上式的 max操作变成取期望。
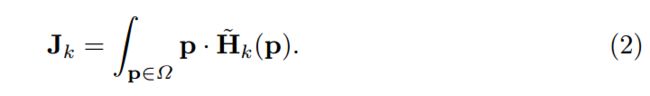
- H ~ k \tilde H_k H~k: 正则化的热图
Ω \Omega Ω: H ~ k \tilde H_k H~k的域
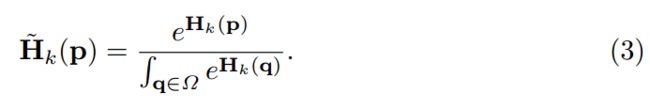
标准化的目的 : 使heatmap中的值全部为正,总和为1,具体原因在【34】中有讨论。
这里使用了softmax函数。
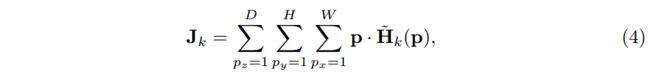
公式4是公式2的离散形式,也就是本文所说 Integral pose regression,有种种优点。 - 可微的,允许端到端训练,
- 快速、非参数化(运算开销小)。
- 它可以很容易地与任何基于热图的方法相结合,
- 潜在的热图表示使其易于训练。
- 它具有连续输出,不存在量化问题
2.1 Joint 3D and 2D training
缺少各种训练数据 是 3D human pose estimation 的一个严重问题。
在将3D和2D训练结合起来方面已经做出了一些努力[55, 31, 43, 51,41]
由于积分回归为二维和三维的姿态估计提供了统一的设置,因此它是一种简单而通用的解决方案,可以促进三维和二维的联合训练,从而解决三维人体姿态估计中的数据问题。
由于式(4)中积分运算的可微性,积分回归自然可以采用这种混合训练技术。我们在实验中也从该技术中得到了巨大的改进,这种改进由于积分公式的存在是可行的
为了使2D数据能够对3D进行监督,我们进一步将积分函数Eq.(4)分解为一个两步的版本,生成单独的x, y, z热图目标。例如,对于x目标,我们首先将三维热图积分为一维x热向量式(5)
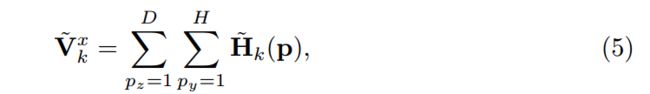
然后将一维x热矢量进一步积分到x关节坐标方程中
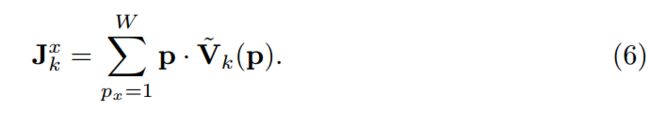
相应的y和z公式应易于推断。这样,x、y、z目标在第一步被分离,允许2D和3D混合数据训练策略。我们从直接和两步积分回归中得到了显著的改善,用于三维姿态估计。
3 Methodology for Comprehensive Experiment
[29, 34] 在 MPII [2] 测试。
[29]只提供系统级比较结果,没有任何消融实验。
[34]研究了热图的归一化方法、热图的正则化和骨干网,但远没有我们研究的那么全面。
Tasks.
我们的方法是通用的,并准备好二维和三维姿态估计任务。从这两个任务中都得到了一致的改进。特别是二维和三维数据在训练中可以很容易地同时混合。3D任务从这项技术中获益更多,并大大超过了以前的工作。
Network Architecture.
我们使用一个简单的网络架构,广泛应用于其他视觉任务,如目标检测和分割[20, 19].
它由一个深度卷积backbone网和一个浅的head网络组成,前者用于从输入图像中提取卷积特征,后者用于从特征中估计目标输出(热图或关节)
实验结果表明,该方法是一种灵活的构件,可以方便地嵌入到各种主干网中,其结果受网络容量的影响比热图小。
- 网络设计 :ResNet[20]和HourGlass[33]、
- 网络深度: ResNet18、50、101[20]、
- 多级设计:[49,7]。
Heat Map Losses
常用:mean squared error (or L2 distance) between the predicted heat map and ground-truth heat map with a 2D Gaussian blob centered on the ground truth joint location
[48, 49, 6, 33, 10, 12, 13, 5]
本文选择 标准差 σ = 1 \sigma = 1 σ=1的Gaussian blob ,同[33],
用 H 1 H1 H1表示该baseline 的loss
其他做法:Mask RCNN work [19] 使用 one-hot m × m ground truth mask
只有一个单独位置被标记为关键点。uses the cross-entropy loss over an m2-way softmax output.
用 H 2 H2 H2表示该baseline 的loss
[38, 22, 36]解决一个逐像素二值分类问题。每个节点的真值热图是通过在内部的每个位置分配一个到真值节点的距离为15像素正标签1来构建的 ,其余负标签为0。
用 H 3 H3 H3表示该baseline 的loss
在实验中,我们证明我们的方法可以很好地处理这些热图损失。虽然这些手工设计的热图损耗在不同的任务上可能会有不同的性能,需要单独进行细致的网络超参数调优,但是他们的 integral version( I 1 、 I 2 、 I 3 I_1、I_2、I_3 I1、I2、I3)将得到显著的改进,并产生一致的结果。
Heat Map and Joint Loss Combination.
对于关节坐标损失,我们将预测关节与真值关节之间的L1和L2距离作为损失函数进行了实验。我们发现,L1损失比L2表现好。因此,我们在所有的实验中都采用L1损失。
注意:无论有中间/无中间热图损失,积分回归都可以进行训练。
对于不使用热图损失的方法,定义为积分回归方法的一种变体,记作 I ∗ I^* I∗。
网络是相同的,但热图上的损失没有使用,训练监督信号只在关节上,不在热图上。
在实验中,我们发现积分回归在有或没有热图监督的情况下都能很好地工作。最佳性能取决于特定的任务。例如,对于2D任务 I 1 I_1 I1获得最佳性能,而对于3D任务 I ∗ I^* I∗获得最佳性能。
Image and Heat Map Resolutions
由于heat map 的量化误差,图片和热图通常都需求高分辨率, 为了准确性。
(高分辨率有内存、计算上的缺点,尤其3D)
结果表明,该方法对图像和热图分辨率变化具有较强的鲁棒性。
4 Datasets and Evaluation Metrics
在3个数据集上做了测试。
-
Human3.6M [24] :3D human pose 数据集
(对于数据集的介绍略)下面是评估方法- mean per joint position error (MPJPE )
[8, 46, 32, 54, 25, 31, 37, 51, 41, 4, 53,44, 56] - metric PA MPJPE
用Procrustes Analysis[18]进行刚性变换 rigid transformation再计算MPJPE
[51, 41, 8, 4,32, 54]
- mean per joint position error (MPJPE )
-
MPII[3] : 2D 单人姿态数据集 (from Youtube)
evaluation:- Percentage of Correct Keypoints (PCK) metric
预测关键点被认为是正确的,如果它距离真值关键点小于 α 倍的头部长度。
记作 PCKh@α ,常用 [email protected] - 为了高精确度,本文还使用 [email protected] and AUC (area under curve, the averaged PCKh when α varies from 0 to 0.5) 作为评估度量标准。
- Percentage of Correct Keypoints (PCK) metric
-
COCO Keypoint Challenge [28] 室外多人检测、姿态估计挑战,条件不受控制。
- object keypoint similarity (OKS)
The OKS plays the same role as the IoU in object detection. It is calculated from the distance between predicted points and ground truth points normalized by the scale of the person
- COCO评估定义了对象关键点相似度(OKS),并使用超过10个OKS阈值的平均精度(AP)作为主要竞争指标
5 Experiments
Training
- backbone network:
ResNet and HourGlass on Human3.6M and MPII
ResNet-101 on COCO - pre-traning:
ResNet is pre-trained on ImageNet classification dataset [16].
Hourglass from scratch,采用E-3标准差正态分布初始化沙漏和head网络参数。 - head network
- heat map baseline and integral regression:
fully convolutional deconvolution layers (4 × 4 kernel, stride 2)
↓upsample the feature map
resolution (64 × 64 by default) , fixed channel 256(与[19]中一样,)
↓
1×1 conv层生成K个热图。 - regression baseline [7, 42, 55, 56]
average pooling layer
↓
全连接
↓
3K(2K) joint坐标
我们将回归基线表示为R1 (R表示回归)
- heat map baseline and integral regression: