堆——最大堆/最小堆的初始化、增加、删除等基本操作

堆的定义：堆是一种经过排序的完全二叉树或满二叉树，

最大堆：就是不不断变得进行树元素替换，最终是树呈现上面数值最大；

最小堆：就是不不断变得进行树元素替换，最终是树呈现上面数值最小；

 

堆的定义

堆是一种经过排序的完全二叉树或满二叉树，n个元素的序列{k1,k2,…,kn}，当且仅当满足如下关系时被成为堆(1)Ki <= k2i 且 ki <= k2i-1或 (2) Ki >= k2i 且 ki >= k2i-1(i = 1,2,…[n/2])当满足(1)时，为最小堆，当满足(2)时，为最大堆。

满二叉树即除最后一层无任何子节点外，每一层上的所有结点都有两个子结点的二叉树。

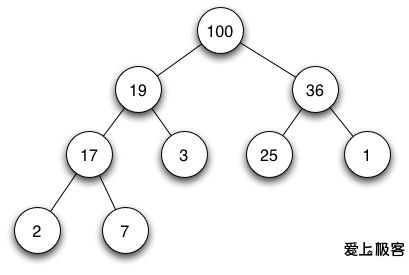
如下为一个最大堆：用数组则可以按顺序表示堆｛100,19,36,17,3,25,1,2,7｝

堆的初始化

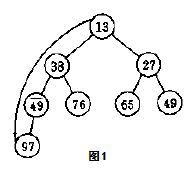
从一个无序序列初始化为一个堆的过程就是一个反复“筛选”的过程。由完全二叉树的性质可以知，一个有n个节点的完全二叉树的最后一个非叶节点是节点[n/2]，堆的初始化过程就从这个[n/2]节点开始。上图为如下无序数组的初始化：

{49,38,65,97,76,13,27,50}

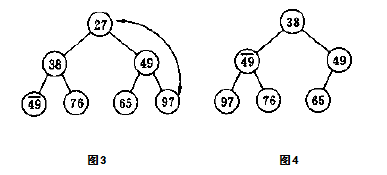
首先，未处理的数组对应的堆为图1模样。从第四个节点开始（[8/2]=4），因为50 < 97，故要交换两节点，交换后还要继续对其新的左子树进行类似输出后那样的筛选。易见其左子树只有节点97，已经为最佳情况，故可以继续堆的初始化，如图2。再考虑第三个节点，因为13 < 27 < 65，即节点13为当前的最小节点，故与节点65交换，并对新的左子树进行筛选，其也为最佳情况，故可继续堆的初始化，结果如图3。然后考虑第二个节点，因为38 < 50 < 76，故已经为最优情况，不用调整。最后再考虑第一个节点，根节点。因为 13 < 38 < 49，故需要将根节点49与其右孩子节点13交换，交换后还要继续对其新的右子树进行类似输出后那样的筛选，可见右子树还需要调整，因为 27 < 49 < 65,故将节点49与节点27交换。此时已经处理完了根节点，初始化结束。最终结果如图5.

void Initialize(T a[], int size, int ArraySize)  
{  
    delete []heap;  
    isExist = false;  
    heap = a;  
    CurrentSize = size;  
    MaxSize = ArraySize;  
    //产生一个最大堆  
    for(int i = CurrentSize / 2; i >= 1; i --)  
    {  
        T y = heap[i];          //子树的根  
        //寻找放置y的位置  
        int c = 2 * i; //c的父节点是y的目标位置  
        while(c <= CurrentSize)  
        {  
            //heap[c］应是较大的同胞节点  
            if(c < CurrentSize && heap[c] < heap[c + 1])  
                c ++;  
            //能把y放入heap[c / 2]吗？  
            if(y >= heap[c])  
                break;          //能               
            else            //不能  
            {  
                heap[c / 2] = heap[c];      //将孩子上移  
                c *= 2;  
            }           //下移一层  
        }  
        heap[c / 2] = y;  
    }  
}

堆的插入

最大堆的插入的思想就是先在最后的结点添加一个元素，然后沿着树上升。跟最大堆的初始化大致相同。

MaxHeap &Insert(const T&x)  
    {     
        if(CurrentSize == MaxSize)  
            exit(1);        //没有足够空间  
  
        //为x寻找应插入位置  
        //i从新的叶节点开始，并沿着树上升  
        int i = ++ CurrentSize;  
        while(i != 1 && x > heap[i/2])  
        {  
            //不把x放进heap[i]  
            heap[i] = heap[i/2];        //元素下移  
            i /= 2;     //移向父节点  
        }  
        heap[i] = x;        //这时候才把x放进去  
        return *this;  
    }

堆的输出

图1为一个最小堆，当最小节点根节点13输出后，将最后一个节点97作为根节点，移到顶端，如图2. 然后要对堆进行调整。比较此完全树的根节点与其两个子节点大小，因为27 < 38 < 97，所以27是三个节点里最小的，将节点27与根节点97交换。此时以97替代27而产生的右子树为一个新的堆，再以97为根节点，对此最小堆进行调整，同理，知道要将97与49交换，得到图3的完全树。此时以97代替49为根节点的右子树为一个新堆，再对此堆做同样的操作，因为此完全树已经是最小堆，所以可以停止操作，堆的调整完毕。此时再将根节点，对的最小值输出，并进行同样的调整，可以得到如图4的新堆。这个过程被称为“筛选”。

简而言之： 最大堆的删除，即删除最大的元素。我们先取第一个元素并删除，然后将最后的元素提到根结点（即第一个元素），然后再把新的根节点放到合适的位置

MaxHeap &DeleteMax(T &x)  
    {  
        //检查堆是否为空  
        if(CurrentSize == 0)  
            exit(1);        //队列空  
  
        x = heap[1];        //最大元素  
        T y = heap[CurrentSize--];      //最后一个元素  
        //从根开始，重构大堆  
        int i = 1, ci = 2;      //ci为i的儿子  
        while(ci < CurrentSize)  
        {  
            if(ci < CurrentSize && heap[ci] < heap[ci + 1])           //比较两个子节点大小，取其大  
                ci ++;  
            //能否放y  
            if(heap[ci] > y)     //不能  
            {  
                heap[i] = heap[ci];     //孩子上移  
                i = ci;                 //下移一层  
                ci *= 2;  
            }  
            else            //能  
                break;  
        }  
        heap[i] = y;  
        return *this;  
    }

---

总结：

初始化：从中间n/2位置从下往上遍历。

增加：从下往上 类似初始化。

输出：最后一个移动到第一个，从上往下遍历。

应用：

堆（通常是二叉堆）常用于排序。这种算法称作堆排序。