图(邻接矩阵实现)(C++实现)
一、实验要求
设计图(网)的邻接矩阵,编写算法实现下列问题的求解。
1.打印出图(网)的两种遍历序。
实验测试数据基本要求:
第一组数据: udg8.grp
第二组数据: udg115.grp
第三组数据: dg6.grp
2.求给定图中的边(或弧)的数目。 实验测试数据基本要求:
第一组数据: udg8.grp
第二组数据: udg115.grp
3.对给定的图G及出发点v0,设计算法从V0出发深度优先遍历图G,并构造出相应的生成树或生成森林。
实验测试数据基本要求:
第一组数据: udg8.grp
第二组数据: dg6.grp
第三组数据: udg114.grp
4.对给定的图G及出发点v0,设计算法从V0出发广度优先遍历图G,并构造出相应的生成树或生成森林。
第一组数据: udg8.grp
第二组数据: dg6.grp
第三组数据: udg114.grp
5.实现Prim算法,求解下列给定图G的最小生成树。 实验测试数据基本要求:第一组数据: udn6.grp
第二组数据: udn8.grp
6.实现Kruskal算法,求解下列给定图G的最小生成树。 实验测试数据基本要求:
第一组数据: udn6.grp
第二组数据: udn8.grp
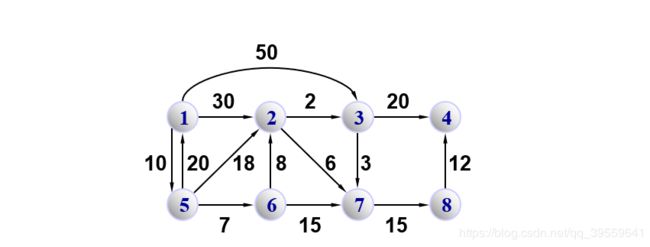
7.实现Dijkstra算法,求解下列给定图G指定顶点到其余顶点之间的最短路径。 实验测试数据基本要求
第一组数据: udn8.grp
第二组数据: dn8.grp
8.实现Floyd算法,求解下列给定图G各顶点之间的最短路径。 实验测试数据基本要求:
第一组数据: udn8.grp
第二组数据: dn8.grp
9.设计算法求解下列给定图G的拓扑序列。 实验测试数据基本要求:
第一组数据: dn8.grp
第二组数据: kPath101.grp
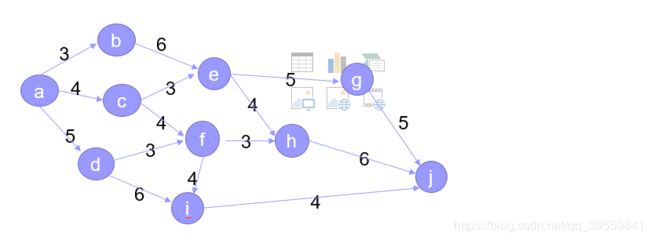
10.设计算法求解下列给定AOE网的关键路径。 实验测试数据基本要求:
第一组数据: dn8.grp
第二组数据: kPath101.grp
二、数据结构设计
//图的邻接矩阵结构:
#define MaxVerNum 100 //定义最大顶点个数
typedef char elementType; //定义图中顶点的数据类型
typedef int cellType; //定义邻接矩阵中元素的数据类型
typedef enum{UDG, UDN, DG, DN} GraphKind; //枚举图的类型
typedef struct GraphAdjMatrix
{
elementType Data[MaxVerNum+1]; //顶点数组,存放顶点元素的值,Data[0]单元不用
cellType AdjMatrix[MaxVerNum+1][MaxVerNum+1]; //邻接矩阵,数组下标为0单元不用,从AdjMatrix[1][1]单元开始
int VerNum; //顶点数
int ArcNum; //弧(边)数
GraphKind gKind; //图的类型:0-无向图;1-无向网;2-有向图;3-有向网
} Graph; //图的类型名
三、算法设计
由于图的深度优先遍历(DFS)、广度优先遍历(BFS)、Prim算法及思想、Kruskal算法及思想、Dijkstra算法及思想、Floyd算法及思想、拓扑序列算法及思想、AOE网的关键路径算法思想书中已给出,这里不再赘述。
- 深度优先遍历生成树算法及思想:修改深度优先遍历树和深度优先遍历森林算法。DFSTree()按照DFS()深度遍历相应递归生成孩子-兄弟表示的二叉树。而DFSForest()则分别处理每棵树,进而转化成森林(二叉链表表示)。算法描述:
//深度优先遍历生成树
void DFSTree(Graph &G,int v,csTree&T)
{
int j,w,first=1; //first标记是否为根节点,初始化为1
csNode *p,*q;
q=T;
visited[v]=1;
w=firstAdj(G,v);
while(w!=0) //还存在邻接点
{
if(!visited[w]&&G.AdjMatrix[v][w]>=1 && G.AdjMatrix[v][w]firstChild=NULL;
p->nextSibling=NULL;
p->data=G.Data[w];
if(first) //(生成第一个孩子)
{
T->firstChild=p;
first=0;
}
else{ //(生成节点的兄弟节点)
q->nextSibling=p;
}
q=p;
DFSTree(G,w,q); //递归处理每个节点
}
w=nextAdj(G,v,w);
}
}
//深度优先遍历生成森林
csTree DFSForest(Graph &G,csTree &T,int v)
{ //v指定生成树或森林的根节点
int i;
csNode *p;
csTree q;
T=NULL;
for(i=1;i<=G.VerNum;i++) //初始化visited数组
{
visited[i]=0;
}
for(v;v>=1;v--) //编号1到v
{
if(!visited[v] )
{
p=new csNode;
p->firstChild=NULL;
p->nextSibling=NULL;
p->data=G.Data[v];
if(!T) //为根节点
{
T=p;
q=T;
}
else{ //生成数根节点的兄弟节点,也就是其他树的根节点
q->nextSibling=p;
}
q=p;
DFSTree(G,v,p);
}
}
for(v+=1;v<=G.VerNum;v++) //编号v到G.vernum
{
if(!visited[v] )
{
p=new csNode;
p->firstChild=NULL;
p->nextSibling=NULL;
p->data=G.Data[v];
if(!T) //为根节点
{
T=p;
q=T;
}
else{ //生成数根节点的兄弟节点,也就是其他树的根节点
q->nextSibling=p;
}
q=p;
DFSTree(G,v,p); //处理每棵树
}
}
return T;
} - 广度优先遍历生成树算法及思想:修改广度优先遍历树和广度优先遍历森林算法。BFSTree()按照BFS()广度遍历相应分层生成孩子-兄弟表示的二叉树。而BFSForest()则分别处理每棵树,进而转化成森林(二叉链表表示)。
算法描述:
//广度优先遍历生成树
void BFSTree(Graph &G,csTree&T,int v)
{
int i,w;
bool first=true; //标志变量,判断是否生成孩子节点
csNode *t,*q,*p;
queue Q;
if(!T) //生成树的根节点
{
T=new csNode;
T->data=G.Data[v];
visited[v]=true;
T->firstChild=T->nextSibling=NULL;
}
p=T;
Q.push(v);
//对其他层节点操作
while(!Q.empty())
{
v=Q.front(); //获取队头编号
Q.pop(); //并出队
w=firstAdj(G,v);
first=true; //循环i层时需要把first置为true,以便生成T->firstChild
while(w!=0)
{
if(!visited[w]&& G.AdjMatrix[v][w]>=1 && G.AdjMatrix[v][w]data=G.Data[w];
q->firstChild=q->nextSibling=NULL;
if(first) //生成孩子节点
{
p->firstChild=q;
first=false;
}
else{ //生成兄弟节点
p->nextSibling=q;
}
p=q;
}
w=nextAdj(G,v,w);
}
}
} 广度优先生成森林与深度优先生成森林代码处理相同,故不再赘述。
四、代码实现
#ifndef _GRPADJMATRIX_H_
#define _GRPADJMATRIX_H_
#include
using namespace std;
//************************************************************//
//* 图的邻接矩阵存储的头文件,文件名:grpAdjMatrix.h *//
//* *//
//************************************************************//
#define INF 65535 //定义无穷大
#define MaxVerNum 100 //定义最大顶点个数
//typedef int elementType; //定义图中顶点的数据类型
typedef char elementType; //定义图中顶点的数据类型
typedef int cellType; //定义邻接矩阵中元素的数据类型
//对无权图,1-相邻(有边),0-不相邻(无边)
//对有权图,为边的权值,特别是无穷大。
//枚举图的类型--无向图(UDG),无向网(UDN),有向图(DG),有向网(DN)
typedef enum{UDG, UDN, DG, DN} GraphKind;
bool visited[MaxVerNum+1]; //全局数组,标记顶点是否已经访问,visited[0]单元不用
//****************************************************//
//* 定义邻接矩阵表示的图结构。5个分量组成: *//
//* data[]数组保存图中顶点数据元素 *//
//* AdjMatrix[][]邻接矩阵 *//
//* VerNum顶点个数 *//
//* ArcNum边(弧)条数 *//
//* gKind枚举图的类型 *//
//* 考虑到名称的统一性,图类型名称定义为Graph *//
//****************************************************//
typedef struct GraphAdjMatrix
{
elementType Data[MaxVerNum+1]; //顶点数组,存放顶点元素的值,Data[0]单元不用
cellType AdjMatrix[MaxVerNum+1][MaxVerNum+1]; //邻接矩阵,数组下标为0单元不用,从AdjMatrix[1][1]单元开始
int VerNum; //顶点数
int ArcNum; //弧(边)数
GraphKind gKind; //图的类型:0-无向图;1-无向网;2-有向图;3-有向网
} Graph; //图的类型名
//******************* 访问图中顶点的函数*********************//
//* 函数功能:打印图中顶点元素,并标记为已经访问 *//
//* 入口参数 Graph G,待访问的图;int verID 目标顶点编号 *//
//* 出口参数:无 *//
//* 返 回 值:空 *//
//* 函 数 名:visit(Graph &G, int verID) *//
//***********************************************************//
void visit(Graph &G, int verID)
{ //顶点编号从1开始,数组0单元不用
cout<=1)&&(G.AdjMatrix[v][w])=1) && (G.AdjMatrix[v][k]) #ifndef _CREATEGRPADJMATRIX_H_
#define _CREATEGRPADJMATRIX_H_
#include "grpAdjMatrix.h"
#include
#include
#include
using namespace std;
void strLTrim(char* str);
//*************************从数据文件创建图**************************//
//* 函数功能:从文本文件创建邻接矩阵表示的图 *//
//* 入口参数 char fileName[],文件名 *//
//* 出口参数: *//
//* 返 回 值:bool,true创建成功;false创建失败 *//
//* 函 数 名:CreateGrpFromFile(char fileName[]) *//
//*******************************************************************//
bool CreateGrpFromFile(char fileName[], Graph &G)
{
FILE* pFile; //定义顺序表的文件指针
char str[1000]; //存放读出一行文本的字符串
char strTemp[10]; //判断是否注释行
cellType eWeight; //边的信息,常为边的权值
GraphKind GrpType; //图类型枚举变量
pFile=fopen(fileName,"r");
if(!pFile)
{
printf("错误:文件%s打开失败。\n",fileName);
return false;
}
while(fgets(str,1000,pFile)!=NULL)
{
//删除字符串左边空格
strLTrim(str);
if (str[0]=='\n') //空行,继续读取下一行
continue;
strncpy(strTemp,str,2);
if(strstr(strTemp,"//")!=NULL) //跳过注释行
continue;
else //非注释行、非空行,跳出循环
break;
}
//循环结束,str中应该已经是文件标识,判断文件格式
if(strstr(str,"Graph")==NULL)
{
printf("错误:打开的文件格式错误!\n");
fclose(pFile); //关闭文件
return false;
}
//读取图的类型,跳过空行
while(fgets(str,1000,pFile)!=NULL)
{
//删除字符串左边空格
strLTrim(str);
if (str[0]=='\n') //空行,继续读取下一行
continue;
strncpy(strTemp,str,2);
if(strstr(strTemp,"//")!=NULL) //注释行,跳过,继续读取下一行
continue;
else //非空行,也非注释行,即图的类型标识
break;
}
//设置图的类型
if(strstr(str,"UDG"))
GrpType=UDG; //无向图
else if(strstr(str,"UDN"))
GrpType=UDN; //无向网
else if(strstr(str,"DG"))
GrpType=DG; //有向图
else if(strstr(str,"DN"))
GrpType=DN; //有向网
else
{
printf("错误:读取图的类型标记失败!\n");
fclose(pFile); //关闭文件
return false;
}
//读取顶点元素,到str。跳过空行
while(fgets(str,1000,pFile)!=NULL)
{
//删除字符串左边空格
strLTrim(str);
if (str[0]=='\n') //空行,继续读取下一行
continue;
strncpy(strTemp,str,2);
if(strstr(strTemp,"//")!=NULL) //注释行,跳过,继续读取下一行
continue;
else //非空行,也非注释行,即图的顶点元素行
break;
}
//顶点数据放入图的顶点数组
char* token=strtok(str," ");
int nNum=1;
while(token!=NULL)
{
G.Data[nNum]=*token; // atoi(token); //顶点数据转换为整数,若为字符则不需转换
token = strtok( NULL, " ");
nNum++;
}
nNum--; //顶点数
//图的邻接矩阵初始化
int nRow=1; //矩阵行下标,从1开始
int nCol=1; //矩阵列下标,从1开始
if(GrpType==UDG || GrpType==DG)
{
for(nRow=1;nRow<=nNum;nRow++)
for(nCol=1;nCol<=nNum;nCol++)
G.AdjMatrix[nRow][nCol]=0;
}
else
{
for(nRow=1;nRow<=nNum;nRow++)
for(nCol=1;nCol<=nNum;nCol++)
G.AdjMatrix[nRow][nCol]=INF; //INF表示无穷大
}
//循环读取边的数据到邻接矩阵
int edgeNum=0; //边的数量
elementType Nf,Ns; //边或弧的2个相邻顶点
while(fgets(str,1000,pFile)!=NULL)
{
//删除字符串左边空格
strLTrim(str);
if (str[0]=='\n') //空行,继续读取下一行
continue;
strncpy(strTemp,str,2);
if(strstr(strTemp,"//")!=NULL) //注释行,跳过,继续读取下一行
continue;
char* token=strtok(str," "); //以空格为分隔符,分割一行数据,写入邻接矩阵
if(token==NULL) //分割为空串,失败退出
{
printf("错误:读取图的边数据失败!\n");
fclose(pFile); //关闭文件
return false;
}
Nf=*token; //获取边的第一个顶点
token = strtok( NULL, " "); //读取下一个子串,即第二个顶点
if(token==NULL) //分割为空串,失败退出
{
printf("错误:读取图的边数据失败!\n");
fclose(pFile); //关闭文件
return false;
}
Ns=*token; //获取边的第二个顶点
//从第一个顶点获取行号
for(nRow=1;nRow<=nNum;nRow++)
{
if(G.Data[nRow]==Nf) //从顶点列表找到第一个顶点的编号
break;
}
//从第二个顶点获取列号
for(nCol=1;nCol<=nNum;nCol++)
{
if(G.Data[nCol]==Ns) //从顶点列表找到第二个顶点的编号
break;
}
//如果为网,读取权值
if(GrpType==UDN || GrpType==DN)
{
token = strtok( NULL, " "); //读取下一个子串,即边的附加信息,常为边的权重
if(token==NULL) //分割为空串,失败退出
{
printf("错误:读取图的边数据失败!\n");
fclose(pFile); //关闭文件
return false;
}
eWeight=atoi(token); //取得边的附加信息
}
if(GrpType==UDN || GrpType==DN) //如果为网,邻接矩阵中对应的边设置权值,否则置为1
G.AdjMatrix[nRow][nCol]=eWeight;
else
G.AdjMatrix[nRow][nCol]=1; //atoi(token); //字符串转为整数
edgeNum++; //边数加1
}
G.VerNum=nNum; //图的顶点数
if(GrpType==UDG || GrpType==UDN)
G.ArcNum=edgeNum / 2; //无向图或网的边数等于统计的数字除2
else
G.ArcNum=edgeNum;
G.gKind=GrpType; //图的类型
fclose(pFile); //关闭文件
return true;
}
//删除字符串、字符数组左边空格
void strLTrim(char* str)
{
int i,j;
int n=0;
n=strlen(str)+1;
for(i=0;i #ifndef _TREE_H_
#define _TREE_H_
#include
#include
using namespace std;
//树(森林)的孩子兄弟链表表示
typedef char elementType;
typedef struct csNode
{
elementType data;
struct csNode *firstChild, *nextSibling;
}csNode,*csTree;
//先序遍历森林
void perOrderTraverse(csNode *T)
{
if(T)
{
cout<data<<" "; //访问根节点
perOrderTraverse(T->firstChild); //递归调用先序遍历左子树
perOrderTraverse(T->nextSibling); //递归调用先序遍历右子树
}
}
//后序遍历森林
void postOrderTraverse(csNode *T)
{
if(T)
{
postOrderTraverse(T->firstChild); //递归调用先序遍历左子树
postOrderTraverse(T->nextSibling); //递归调用先序遍历右子树
cout<data<<" "; //访问根节点
}
}
//层次遍历森林
void levelOrderTraverse(csNode *T)
{
queue q;
csNode * u,*n,*p;
if(T==NULL)
{
return;
}
n=T;
while(n)
{
p=n;
q.push(p);
while(!q.empty())
{
p=q.front();
cout<data<<" ";
u=p->firstChild;
while(u)
{
p=u;
q.push(p);
u=u->nextSibling;
}
q.pop();
}
n=n->nextSibling;
}
}
//销毁森林
void destroy(csNode *&T)
{
if(T)
{
destroy(T->firstChild);
destroy(T->nextSibling);
delete T;
}
}
#endif // _TREE_H_ #ifndef _OPERATEGRPADJMATRIX_H_
#define _OPERATEGRPADJMATRIX_H_
#include
#include
#include
#include "grpAdjMatrix.h"
#include "tree.h"
using namespace std;
//定义边集(prim)
typedef struct minEdgeType{
int v; //边中已选顶点一端
cellType eWeight; //边的权重
} MinEdgeType;
//定义边集(kruskal)
typedef int eInfoType;
typedef struct edgetype{
int vBeign;
int vEnd;
eInfoType eWeight;
}EdgeType;
//操作菜单
void menu()
{
cout<<"*************************************************"<=1 && G.AdjMatrix[v][w]=1;v--) //编号1到v
{
if(visited[v]==false) //循环选择未被访问的顶点
DFS(G,v); //每次循环遍历一个连通分量
}
for(v;v<=G.VerNum;v++) //编号v到G.vernum
{
if(visited[v]==false) //循环选择未被访问的顶点
DFS(G,v); //每次循环遍历一个连通分量
}
}
//连通图的广度优先遍历
void BFS(Graph &G,int v)
{
queue Q; //队列存放元素的编号
int w;
visit(G,v); //访问定点,并设置其访问标志
Q.push(v); //节点编号入队
while(!Q.empty())
{
v=Q.front();
Q.pop();
w=firstAdj(G,v);
while(w!=0)
{
if(!visited[w] && G.AdjMatrix[v][w]>=1 && G.AdjMatrix[v][w]=1;v--) //编号1到v
{
if(visited[v]==false) //循环选择未被访问的顶点
BFS(G,v); //每次循环遍历一个连通分量
}
for(v;v<=G.VerNum;v++) //编号v到G.vernum
{
if(visited[v]==false) //循环选择未被访问的顶点
BFS(G,v); //每次循环遍历一个连通分量
}
}
//深度优先遍历生成树
void DFSTree(Graph &G,int v,csTree&T)
{
int j,w,first=1; //first标记是否为根节点,初始化为1
csNode *p,*q;
q=T;
visited[v]=1;
w=firstAdj(G,v);
while(w!=0) //还存在临结点
{
if(!visited[w] && G.AdjMatrix[v][w]>=1 && G.AdjMatrix[v][w]firstChild=NULL;
p->nextSibling=NULL;
p->data=G.Data[w];
if(first) //(生成第一个孩子)
{
T->firstChild=p;
first=0;
}
else{ //(生成节点的兄弟节点)
q->nextSibling=p;
}
q=p;
DFSTree(G,w,q); //递归处理每个节点
}
w=nextAdj(G,v,w);
}
}
//深度优先遍历生成森林
csTree DFSForest(Graph &G,csTree &T,int v)
{
int i;
csNode *p;
csTree q;
T=NULL;
for(i=1;i<=G.VerNum;i++) //初始化visited数组
{
visited[i]=0;
}
for(v;v>=1;v--) //编号1到v
{
if(!visited[v] )
{
p=new csNode;
p->firstChild=NULL;
p->nextSibling=NULL;
p->data=G.Data[v];
if(!T) //为根节点
{
T=p;
q=T;
}
else{ //生成数根节点的兄弟节点,也就是其他树的根节点
q->nextSibling=p;
}
q=p;
DFSTree(G,v,p);
}
}
for(v+=1;v<=G.VerNum;v++) //编号v到G.vernum
{
if(!visited[v] )
{
p=new csNode;
p->firstChild=NULL;
p->nextSibling=NULL;
p->data=G.Data[v];
if(!T) //为根节点
{
T=p;
q=T;
}
else{ //生成数根节点的兄弟节点,也就是其他树的根节点
q->nextSibling=p;
}
q=p;
DFSTree(G,v,p);
}
}
return T;
}
//广度优先遍历生成树
void BFSTree(Graph &G,csTree&T,int v)
{
int i,w;
bool first=true; //标志变量,判断是否生成孩子节点
csNode *t,*q,*p;
queue Q;
if(!T) //生成树的根节点
{
T=new csNode;
T->data=G.Data[v];
visited[v]=true;
T->firstChild=T->nextSibling=NULL;
}
p=T;
Q.push(v);
//对其他层节点操作
while(!Q.empty())
{
v=Q.front(); //获取队头编号
Q.pop(); //并出队
w=firstAdj(G,v);
first=true; //循环i层时需要把first置为true,以便生成T->firstChild
while(w!=0)
{
if(!visited[w]&& G.AdjMatrix[v][w]>=1 && G.AdjMatrix[v][w]data=G.Data[w];
q->firstChild=q->nextSibling=NULL;
if(first) //生成孩子节点
{
p->firstChild=q;
first=false;
}
else{ //生成兄弟节点
p->nextSibling=q;
}
p=q;
}
w=nextAdj(G,v,w);
}
}
}
//广度优先遍历生成森林
csTree BFSForest(Graph &G,csTree&T,int v)
{
int i;
csNode *p;
csTree q;
T=NULL;
for(i=1;i<=G.VerNum;i++) //初始化visited数组
{
visited[i]=0;
}
for(v;v>=1;v--) //编号1到v
{
if(!visited[v] )
{
visited[v]=true; //标记已访问
p=new csNode;
p->firstChild=NULL;
p->nextSibling=NULL;
p->data=G.Data[v];
if(!T) //为根节点
{
T=p;
q=T;
}
else{ //生成数根节点的兄弟节点,也就是其他树的根节点
q->nextSibling=p;
}
q=p;
BFSTree(G,p,v);
}
}
for(v+=1;v<=G.VerNum;v++) //编号v到G.vernum
{
if(!visited[v] )
{
visited[v]=true; //标记已访问
p=new csNode;
p->firstChild=NULL;
p->nextSibling=NULL;
p->data=G.Data[v];
if(!T) //为根节点
{
T=p;
q=T;
}
else{ //生成数根节点的兄弟节点,也就是其他树的根节点
q->nextSibling=p;
}
q=p;
BFSTree(G,p,v);
}
}
return T;
}
//判断两个顶点是否有边
bool HasEdge(Graph &G,int vBegin ,int vEnd,int &eWeight)
{
int f=false;
if(G.AdjMatrix[vBegin][vEnd]!=INF)
{
eWeight=G.AdjMatrix[vBegin][vEnd];
f=true;
return f;
}
else{
eWeight=G.AdjMatrix[vBegin][vEnd];
return f;
}
}
//初始化候选边集
void initTE(Graph &G,MinEdgeType TE[],int vID)
{
int i;
int eWeight;
for(i=1;i<=G.VerNum;i++)
{
//初始化数组
if(HasEdge(G,vID,i,eWeight)) // 顶点和i有边
{
TE[i].v=vID;
TE[i].eWeight=eWeight;
}
else{
TE[i].eWeight=INF;
}
}
}
//得到候选边集的最小边
int getMinEdge(Graph &G,MinEdgeType TE[])
{
int eMin=INF;
int i,j=0;
for(i=1;i<=G.VerNum;i++)
{
if(visited[i]==false && TE[i].eWeight=0;j--)
{
cout<=0;k--)
{
cout<0 && G.AdjMatrix[j][i] S; //定义一个顺序栈,保存入度为0的节点
int i;
int v; //顶点编号
int vCount=0; //记录顶点入度为0的顶点数
for(i=1;i<=G.VerNum;i++) //初始化vet[]数组
{
vet[i]=0;
}
for(i=1;i<=G.VerNum;i++) //入度数组初始化,inds[0]不用
{
inds[i]=0;
}
for(i=1;i=1 && G.AdjMatrix[v][i] vet[i])
{
vet[i]=vet[v]+G.AdjMatrix[v][i]; //求其v的邻接顶点最早发生时间
}
}
}
}
if(vCount==G.VerNum)
return 1; //返回无回路标记
else
return 0;
}
//输出拓扑序列
void printTopoList(Graph &G,int topoList[],int vet[])
{
int i;
if(TopologicalSort(G,topoList,vet))
{
cout<<"拓扑序列为:";
for(i=0;i0 && G.AdjMatrix[i][j] S; //保存出度为0的顶点
int i;
int v; //顶点编号
int vCount=0; //记录顶点入度为0的顶点数
int max=0;
for(i=1;i<=G.VerNum;i++)
{
if(max=1 && G.AdjMatrix[i][v]=1 && G.AdjMatrix[k][j] < INF)
{
if(vet[j]==vlt[j])
{
break;
}
}
}
}
k=j; //或取k的邻接点
}
}
#endif // _OPERATEGRPADJMATRIX_H_ #include
#include
#include "createGrpAdjMatrix.h"
#include "operateGrpAdjMatrix.h"
#include "tree.h"
using namespace std;
int main()
{
int i,x;
Graph G;
csTree T;
int path[MaxVerNum];
int dist[MaxVerNum];
int topoList[MaxVerNum]; //拓扑序列
int antiTopoList[MaxVerNum]; //逆拓扑序列
cellType Dist[MaxVerNum][MaxVerNum];
int Path[MaxVerNum][MaxVerNum];
int vet[MaxVerNum]={0}; //事件的最早发生时间
int vlt[MaxVerNum]={0}; //事件的最晚发生时间
char fileName[100]; //保存文件名
menu();
cout<<"请输入执行序号:";
cin>>i;
while(i)
{
switch(i)
{
case 1:
cout<<"请输入打开的文件名:";
cin>>fileName;
if(CreateGrpFromFile(fileName,G))
{
cout<<"数据处理完毕!"<>x;
cout<<"深度优先遍历序为:";
DFSTraverse(G,x);
cout<>x;
T=DFSForest(G,T,x);
cout<<"树或森林的先序遍历序为:";
perOrderTraverse(T);
cout<>x;
T=BFSForest(G,T,x);
cout<<"树或森林的先序遍历序为:";
perOrderTraverse(T);
cout<>x;
prim(G,x);
cout<>x;
Dijkstra(G,path,dist,x);
printDijsktra(G,path,dist,x);
break;
case 9:
floyd(G,Dist,Path);
printFloyd(G,Dist,Path);
break;
case 10:
printTopoList(G,topoList,vet);
cout<>i;
}
return 0;
}
五、运行和测试
本实验所需文件和代码可从百度网盘进行下载:https://pan.baidu.com/s/19Rcf5faJNDj8NFC74hlcrA 提取码:y5ap