深度前馈神经网络之深度神经网络（DNN）总结

一、深度前馈神经网络概览

多层感知机（MLP）和深度神经网络（DNN）是一样的模型，只是叫法不同。
深度神经网络（DNN），卷积神经网络（CNN）都属于深度前馈神经网络（DFNN）。这一部分主要讲全连接网络，下一部分讲卷积神经网络CNN。

• 全连接，MLP，DNN采用，当前层的单元与上一层的每一个单元都有连接。
• 稀疏连接，CNN采用，当前层的单元只与上一层的部分单元有连接。

网络结构

输入层–隐藏层（激活函数去线性化、解决异或问题）–输出层–处理层（softmax转换成概率分布）–最终输出层

二、深度神经网络（全连接网络）

1、前向传播计算算法

深度神经网络采用全连接网络结构，采用前向传播计算算法，代码如下

import tensorflow as tf

x = tf.constant([0.9, 0.85], shape=[1, 2])

# 使用随机正态分布函数声明w1和w2两个变量，其中w1是2x3的矩阵，w2是3x1的矩阵
# 这里使用了随机种子参数seed，这样可以保证每次运行得到的结果是一样的
w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1), name="w1")
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1), name="w2")

# 将biase(偏置项)参数b1设置为初始值全为0的1x3矩阵，b2是初始值全为1的1x1矩阵
b1 = tf.Variable(tf.zeros([1, 3]))
b2 = tf.Variable(tf.ones([1]))

init_op = tf.global_variables_initializer()

a = tf.nn.relu(tf.matmul(x, w1) + b1)
y = tf.nn.relu(tf.matmul(a, w2) + b2)
with tf.Session() as sess:
    sess.run(init_op)
    print(sess.run(y))

解释：
一般权重参数会初始化为随机矩阵，偏置会初始化全为1或者全为0。

2、激活函数（应用于每一个节点从而去线性化）

通常来说ELU函数>leaky ReLU函数（和它的变种） >ReLU函数>tanh函数>逻辑函数
如果神经网络每一个节点的输出为输入的加权和，那么最后输出将成为一个线性模型,解决不了复杂的问题，所以我们使用激活函数使得每一个节点的输出为非线性，常用激活函数有Relu，Sigmoid，tanh，ELU。

Relu

tf.nn.relu(x, name = None)

函数形式$f(x)=max(0,x)$
加入ReLu激活函数的神经元被称为整流线性单元
图像：

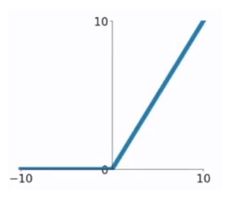
相比sigmod函数与Relu函数，Relu函数有以下优缺点
优点
1)克服梯度消失的问题
2)加快训练速度(克服了梯度消失问题，训练才会快)
3)一阶导数处处相等为1，二阶导数处处为0
4）单侧抑制
缺点：
1)若输入负数，则完全不激活，ReLU函数没用。
2)ReLU函数输出要么是0，要么是正数，也就是ReLU函数不是以0为中心的函数。

Sigmoid

tf.sigmoid(x, name = None)

Sigmoid不被鼓励应用于前馈网络中的隐藏单元，因为sigmoid存在饱和性，导数值会很小。
函数形式$f(x)=\frac{1}{1+e^{-x}}$
当x趋近于负无穷时，y趋近于0；当x趋近于正无穷时，y趋近于1；当x= 0时，y=0.5.
图像

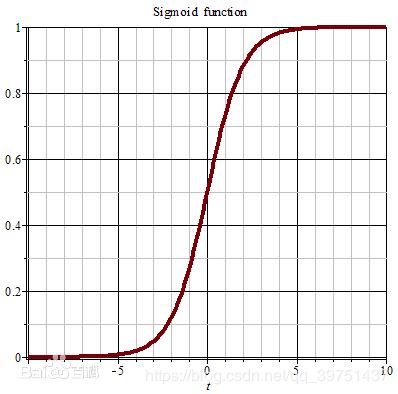
相比sigmod函数与Relu函数，sigmod函数有以下优缺点
优点：
1.Sigmoid函数的输出映射在(0,1)之间，单调连续，输出范围有限，优化稳定，可以用作输出层。
2.求导容易。
缺点：
1.由于其软饱和性，容易产生梯度消失，导致训练出现问题。
2.其输出并不是以0为中心的。
3.激活函数计算量大，反向传播求误差梯度时，求导涉及除法。

tanh

tf.tanh(x, name = None)

函数形式$f(x)=\frac{1-e^{-2x}}{1+e^{-2x}}$
图像

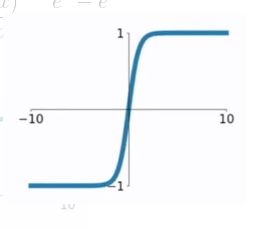
相比sigmod函数与tanh函数

• sigmod函数与tanh函数在输入很大或是很小的时候，输出都几乎平滑，梯度很小，不利于权重更新；
• sigmod函数与tanh函数不同的是输出区间，tanh的输出区间是在(-1,1)之间，而且整个函数是以0为中心的，这个特点比sigmod的好。
• 一般二分类问题中，隐藏层用tanh函数，输出层用sigmod函数。
• tanh是双曲正切函数，tanh函数和sigmod函数的曲线是比较相近的，

ELU

3、损失函数

分类问题和回归问题是监学习的两大类，学习问题需要定义一个损失函数来刻画预测与真实之间的距离，损失函数越小，代表模型得到的结果与真实值偏差越小，模型越精确。介绍两个损失函数

• 交叉熵损失函数，常用于分类问题
• 均方误差损失函数，常用于回归问题

交叉熵函数

定义预测概率分布q(x)向量与真实概率分布p(x)向量估计的准确程度，刻画的是两个概率分布向量的距离，所以要求神经网络输出的是一个概率分布向量

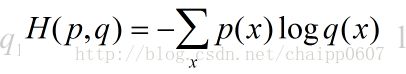
cross_entropy = -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y, 1e-10, 1.0)))

tf.reduce_mean()计算平均值，tf.clip_by_value将张量数值限制在一个范围内，tf.log是取对数，y_是真实分布，y是预测分布。
在使用交叉熵之前，神经网络输出必须为概率向量，所以经常将softmax与交叉熵搭配使用，即tf.nn.softmax_cross_entropy_with_logits()函数，softmax将神经网络输出转为概率分布向量，接下来使用交叉熵损失函数计算损失（即预测概率分布q(x)向量与真实概率分布p(x)向量的距离）
softmax函数

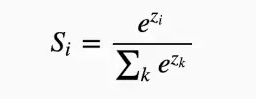
注意;tf.nn.sparse_softmax_cross_entropy_with_logits更适用于只有一个正确答案的分类问题，使用tensorflow代码如下。

cross_entropy = tf.nn.sorfmax_cross_entropy_with_logits(y_ ,y) 

均方误差损失函数

回归模型完成的是对具体数值的预测，神经网络会输出一个预测值，一般只有一个回归节点
公式如下，解决回归问题的网络模型就是以最小化该函数为目标。

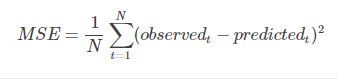
mse=tf.reduce_mean(tf.square(y_-y))